2021.4.2训练

7-1 选夫婿^_^ (20 分)

倾国倾城的大家闺秀潘小姐要选夫婿啦！武林中各门各派，武林外各大户人家，闻讯纷纷前来，强势围观。前来参与竞选的男生藏龙卧虎，高手云集，才子遍布，帅哥纷纭，更不乏富二代，官二代，可谓声势空前。

每个人参与竞选的帅哥除了进行一段激情洋溢的求婚演讲以外，还要报上自己姓名、身高和体重，以及个人简历。最后再进行文武选拔，最后夺魁者方能得到潘小姐的芳心。

潘小姐不爱名利，只看人，第一关就是身高和体重要合格，即必须在其要求的范围内，否则直接排除在外，不允许参加下一轮的选拔。

作为一个程序员，你没有钱也没有权，擅长的也就是编程了。潘小姐也发现了这一点，所以把首轮根据身高体重进行选拔的任务交给了你，如果完成的好，你可以直接进入下一轮选拔，你笑了。

输入格式:

潘小姐给你了所有报名男生的信息。输入数据的第一行是一个正整数N(0 < N < 1000)。然后N行数据，每行包含三部分，用空格隔开。第一部分是报名者的姓名name(长度小于20的字符串)，然后是整数身高h（0 < h < 300），第三部分是整数体重w (0 < w < 200)。

最后一行是四个整数a,b,c,d.表示身高的合格范围是[a,b],体重的合格范围是[c,d]（0 < a < b < 200, 0 < c < d < 300）。

输出格式:

你需要把合格的男生信息按照身高从低到高输出，格式跟输入一样，也是每行三个信息，共N行，如果身高相同则按体重从轻到重输出，如果身高相同并且体重相同则按照输入顺序依次输出，若没有合格人选则输出NO，具体格式见样例。

输入样例:

8
武大郎 70 40
西门庆 180 70
李逵 160 150
燕青 175 69
鲁智深 180 100
武松 180 75
小泉纯一狼 30 20
孙二娘 169 60
165 190 60 90

输出样例:

孙二娘 169 60
燕青 175 69
西门庆 180 70
武松 180 75

思路：无

如果本地IDE乱码的话，不用理它，直接提交

#include<bits/stdc++.h>
using namespace std ;
struct node{
    string name ;
    int h ;
    int w ;
    int id;
};
bool cmp(node a  , node b){
    if(a.h == b.h){
        if(a.w == b.w){
            return a.id < b.id;
        }
        return a.w < b.w;
    }
    return a.h< b.h;
}
int main(){
    int n ;
    cin>>n;
    
    int len = n ;
    int h_t , h_w , w_t , w_w;
    node nums[1001];
    for(int i = 0 ; i < n ; i++){
        cin>>nums[i].name >> nums[i].h>>nums[i].w;
        nums[i].id = i;
    }
    cin>>h_t>>h_w>>w_t>>w_w;
    sort(nums, nums+n , cmp);
    bool flog = false;
    for(int i = 0 ; i < n ; i++){
        if(nums[i].h >= h_t && nums[i].h <= h_w && nums[i].w >= w_t && nums[i].w <= w_w){
            flog = true;
            cout<<nums[i].name<<" "<<nums[i].h<<" "<<nums[i].w<<endl;
        }
    }
    if(!flog) cout<<"NO"<<endl;
    return 0;
}

7-2 乱敲钟 (15 分)

有大小两寺敲晨钟，报时警示时光匆，约定晨时同起声，大寺三分敲一下，小寺四时应一声，大小各敲十二通，一人居在两寺中，可闻多少晨钟声。

上面故事的意思是：有大小两座寺院敲晨钟用来报时，并且两座寺院都是在晨时开始敲钟。大寺院每3分钟敲一下，小寺院每4分钟敲一下，两座寺院各敲12下，居住在两座寺院中间的人能听到多少声钟声？答案很简单，21次。

这个题目太简单了，我们现在想弄个复杂点的。三个寺庙呈品字形排列，一个人站在三个寺庙连成的三角形的中心，离三个寺庙的距离相等。三个寺庙同时从0点开始敲钟，但是和尚每天的规律都不同，如果告诉你每个寺庙每天的敲钟间隔，以及敲钟的总数，你能知道站在中间的人总共能听到多少声钟声吗？

输入格式:

输入在一行中给出4个绝对值不超过1000的整数A，B，C，N，分别代表三个寺庙敲钟的间隔，N则是每个寺庙敲钟的次数。

输出格式:

对每一组输入，在一行中输出站在中间的人听到的钟声次数。

输入样例:

在这里给出一组输入。例如：

3 4 5 3

输出样例:

在这里给出相应的输出。例如：

思路：正解应该是最小公倍数和最大公因数的题（没拿满分，然后直接暴力）

#include<bits/stdc++.h>
using namespace std ;
int main(){
    int a , b , c , n;
    int nums[4];
    int s[4];
    for(int i = 0 ; i < 3 ; i++) cin>>nums[i];
    cin>>n;
    for(int i = 0 ; i < 3 ; i++) s[i] = n;
    int sum = 0 ; 
    for(int i = 0; i < 1000001 ; i++){
        if(s[0] == 0 && s[1] == 0 && s[2] ==0 ) break;
        if(i%nums[0] == 0 && s[0]>0){
            if(i % nums[1] == 0 && s[1] >0 ){
                if(i % nums[2] == 0 && s[2] >0 ){
                    sum += 2 ;
                    s[2]--;
                }
                else {
                    sum ++;
                }
                s[1]--;
            }
            else if(i % nums[2] == 0 && s[2] > 0){
                sum++;
                s[2]--;
            }
            s[0]--;
        }
        else if(i%nums[1] == 0 && s[1]>0){
            if(i % nums[2] == 0 && s[2] >0 ){
                    sum += 1 ;
                    s[2]--;
            }
            s[1]--;
        }
        else if(i%nums[2] == 0 && s[2]>0){
            s[2]--;
        }
    }
    cout<<3*n-sum<<endl;
    return 0;
}

老师给出来的解法：（很妙，直接用容器，过滤掉相同的时间点）

#include <bits/stdc++.h>
using namespace std;
int main()
{
    set<int> bell;
    int i, A, B, C, disA, disB, disC, cnt;
    bell.clear();
    A = 1;
    B = 1;
    C = 1;
    scanf("%d %d %d %d", &disA, &disB, &disC, &cnt);

    for(i = 0; i < cnt; i++)
    {
        bell.insert(A);
        A += disA;
        bell.insert(B);
        B += disB;
        bell.insert(C);
        C += disC;
    }
    printf("%d\n",bell.size());
    return 0;
}

思路：woc , 我手呢？

7-4 阿飞的挺身而出 (10 分)

大林最近看了一些大数计算的资料，觉得颇有心得，于是他在课堂上出了一道简单的大数加法给学生做练习，当然两个加数都是超过int和long所能表示的数的范围。这让他的学生们不禁陷入了沉思，怎么办呢？做不出来的话期末成绩可能要59分了。在这危急时刻，有个聪明的阿飞同学挺身而出，通过仔细观察，他发现两个高位数的正整数相加，可以把这两个正整数分别拆成两个低位数的正整数之间的加法和进位运算。经过不懈努力，他成功地解决了这道题，获得了大林的表扬。请大家向阿飞同学学习，也编写类似程序来解决这个问题。

输入格式:

两个30位正整数。

输出格式:

和

输入样例:

111123456789101112131715161718
222345678910111213141516171819

输出样例:

333469135699212325273231333537

思路：网上有C++的模板，但是我一般都是Java写

import java.math.BigInteger;
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        BigInteger one , two ;
        Scanner cin = new Scanner(System.in);
        one = cin.nextBigInteger();
        two = cin.nextBigInteger();
        System.out.println(one.add(two));
    }
}

未读懂题意，不知道在讲什么

7-6 样本方差 (5 分)

u=3226723262,278720713&fm=15&gp=0.jpg

作为概率论随便考 $1分的你，口算出给定样本的方差自然也不在话下，不过今天需要你编程实现这样的程序。$

样本方差： $($

样本均值：

输入格式:

输入共两行。

第一行为一个正整数 $,，即给定样本的数量。$

第二行为

输出格式:

输出仅 $1 行，为计算出来的样本方差（保留 2 位小数，不足用 0 补齐）。$

输入样例:

4
974 559 974 233

输出样例:

129074.00

#include<bits/stdc++.h>
using namespace std ;


int main(){
    int n ;
    cin>>n;
    int nums[10001];
    for(int i = 0; i < n ; i++) cin>>nums[i];
    int sum = 0 ;
    int p = 0 ;
    for(int i = 0; i < n ; i++){
        p += nums[i];
    }
    double x_ = (1.0/n)*p;
    double S = 0 ;
    for(int i = 0 ; i < n ; i++){
        S += pow(nums[i]-x_ , 2);
    }
    double q = (1.0/(n-1));

    printf("%.2f" , q*S);
    

    return 0;
}

思路：无，按着公式模拟就好了，数据尽量用double，不知道有没有坑呢

7-7 小文的心理阴影时刻 (10 分)

小文十分守时，和别人约会一般会提前k秒钟到，如果对方不准时，他等候k秒钟后也会自行离开。如果称这段时间为小文的心理阴影时间，请编程输出小文的心理阴影时间的起始和结束时刻。

输入格式:

有多组输入数据。先读入一个整数n，接下来包含n行，每行有一个24小时制的时分秒的时间和k秒数

输出格式:

输出心理阴影时间的起始时刻和结束时刻（如果大于等于24:00:00，则从00:00:00开始计数，如果小于00:00:00，则从23:59:59秒开始倒数）

输入样例:

1
12 10 30 40

输出样例:

12:09:50 12:11:10

#include<bits/stdc++.h>
using namespace std ;
int main(){
    int n ;
    cin>>n;
    int h , m , s , k ;
    while(n--){
        cin>>h>>m>>s>>k;
        int sum_time = h*60*60 + m*60 + s ; //转化为s
        int start = sum_time - k;
        int _end = sum_time + k;
        if(_end >= 86400){
            _end -= 86400;
        } 
        if(start < 0){
            start += 86400;
        }
        printf("%02d:%02d:%02d " , start/3600 , (start%3600) / 60 , ((start%3600) % 60 ) ) ;
        printf("%02d:%02d:%02d\n" , _end/3600 , (_end%3600) / 60 , ((_end%3600) % 60 ) );
    }
    return 0;    
}

思路：我只对了一半，（就是时间全转化秒，再加减，然后转化回来输出，有坑点，不知道是哪里，当时也很多人没拿全分）

找到了，不能用ACM中的多组输入while(scanf("%d" , &n) != EOF){ while (n--){ } } 这种格式，第一个测试点答案错误！！

7-8 试题 F：复制粘贴 (20 分)

复制粘贴是文本编辑器最重要的功能之一，JOI 社正在开发一个可以快速处理复制粘贴操作的文本编辑器。作为 JOI 社的一名优秀的程序员，你的任务是测试复制粘贴功能的核心代码。由于JOI 社危在旦夕，你需要确保这段核心代码准确高速。

具体的操作如下。初始时文件内容为一个字符串 $, 随后进行$

给定文本

输入格式:

第一行两个正整数 $, 分别表示最后要输出文本$

第二行一个字符串

第三行一个正整数

接下来

输出格式:

一行一个长度为

输入样例1:

2 18
copypaste
4
3 6 8
1 5 2
4 12 1
17 18 0

输出样例1:

ac

输入输出样例1解释

初始文本为 copypaste。

第一次操作, 将位置 3 到位置 6 之间的文本 ypa 复制到位置 8 , 文本变为 copypastypae。

第二次操作, 将位置 1 到位置 5 之间的文本 opyp 复制到位置 8 , 文本变为 coopyppypastypae。

第三次操作, 将位置 4 到位置 12 之间的文本 yppypast 复制到位置 1 , 文本变为 cyppypastoopyppypastypae。但是文本长度上限 $8 从右向左删除文本中字符至文本长度为 1 文本变为 с уррураs tооруррура。$

第四次操作, 将位置 17 到位置 18 之间的文本 a 复制到位置 0 , 文本变为 acyppypastoopyppypa。但是文本长度上限 $8 从右向左删除文本中字符至文本长度为 18 , 文本变为 acyppypastoopyppyp。$

最终, 输出文本 acyppypastoopyppyp 的前

输入样例2:

输出样例2:

joioji

数据范围与提示

对于全部数据, $1 。保证$

设

#include<bits/stdc++.h>
using namespace std ;


int main(){

    int K,M ;
    cin>>K>>M;
    string str;
    cin>>str;
    
    int n ; 
    cin>>n;
    int a , b ,c ;
    while(n--){
        cin>>a>>b>>c;
        string s="";
        for(int i = a ; i < b ; i++)
            s += str[i];
        string temp = "";
        for(int i = 0 ; i < c ; i++){
            temp += str[i];
        }
        //cout<<"temp = "<<temp<<endl;
        string p = temp ;
        p += s ; 
        int len = p.size();
        for(int i = c ; i<str.size() && i < M  ; i++){
            
            p+=str[i];
            if(p.size() == M) break;
        }
        str = p;
        //cout<<str<<endl;
    }
    for(int i = 0 ; i < K ; i++)
        cout<<str[i];

    return 0;    
}

思路：别想太多，暴力走一波

7-15 数字三角形 (30 分)

观察下面的数字金字塔。写一个程序查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以从当前点走到左下方的点也可以到达右下方的点。

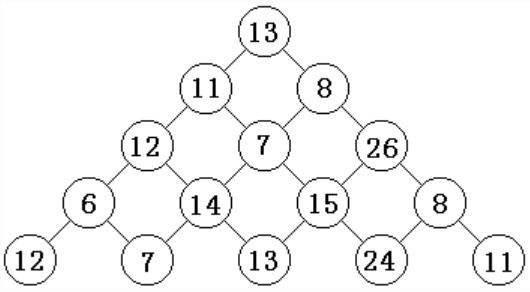
在上面的样例中,从13到8到26到15到24的路径产生了最大的和86。

输入格式:

第一个行包含R(1≤ R≤1000)，表示行的数目。

后面每行为这个数字金字塔特定行包含的整数。

所有的被供应的整数是非负的且不大于100。

输出格式:

单独的一行，包含那个可能得到的最大的和。

输入样例:

5
13
11 8
12 7  26
6  14 15 8
12 7  13 24 11

输出样例:

经典DP入门题

#include<bits/stdc++.h>
using namespace std ;
int nums[1002][1002];

int main(){
    int n ;
    cin>>n;
    memset(nums,0,sizeof(nums));
    for(int i = 1 ; i <= n ; i++){
        for(int j = 1 ; j <= i ; j++){
            cin>>nums[i][j];
        }
    }
    int sum = 0 ; 
    for(int i = 1 ; i <= n ; i++){
        for(int j = 1 ; j <= i ; j++){
            nums[i][j] = max(nums[i-1][j] , nums[i-1][j-1]) + nums[i][j]; ;
        }
    }
    for(int i = 1; i < 1002 ; i++){
        sum = max(sum , nums[n][i]);
    }
    cout<<sum<<endl;
    return 0;    
}

我这个解法，还不太好，内存还能缩一缩

posted @ 2021-04-03 10:21 .李宁宁阅读(1825) 评论(0) 编辑收藏举报

刷新页面返回顶部

.李宁宁

2021.4.2训练

输入格式:

输出格式:

输入样例:

输出样例:

输入格式:

输出格式:

输入样例:

输出样例:

输入格式:

输出格式:

输入样例:

输出样例:

输入格式:

输出格式:

输入样例:

输出样例:

输入格式:

输出格式:

输入样例:

输出样例:

输入格式:

输出格式:

输入样例1:

输出样例1:

输入输出样例1解释

输入样例2:

输出样例2:

数据范围与提示

输入格式:

输出格式:

输入样例:

输出样例:

公告