DTW(动态时间规整)算法原理与应用
参考:https://www.bilibili.com/video/BV12r4y1A7mT/?spm_id_from=333.337.search-card.all.click&vd_source=3ad05e655a5ea14063a9fd1c0dcdee3e

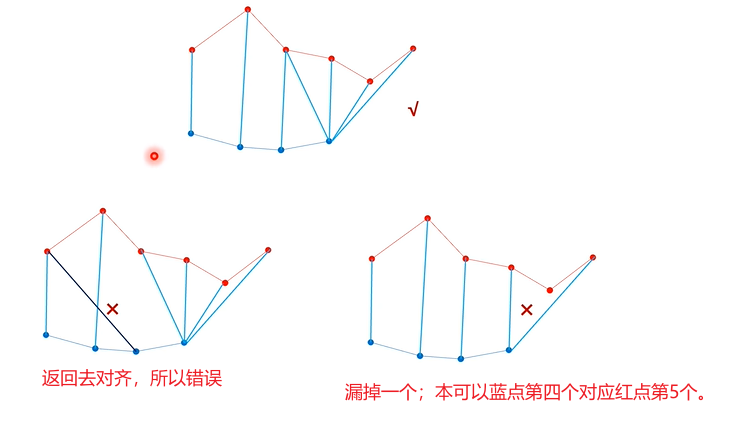
那么如何通过某个算法实现红蓝点的一一对应,且使得平均距离最短呢?
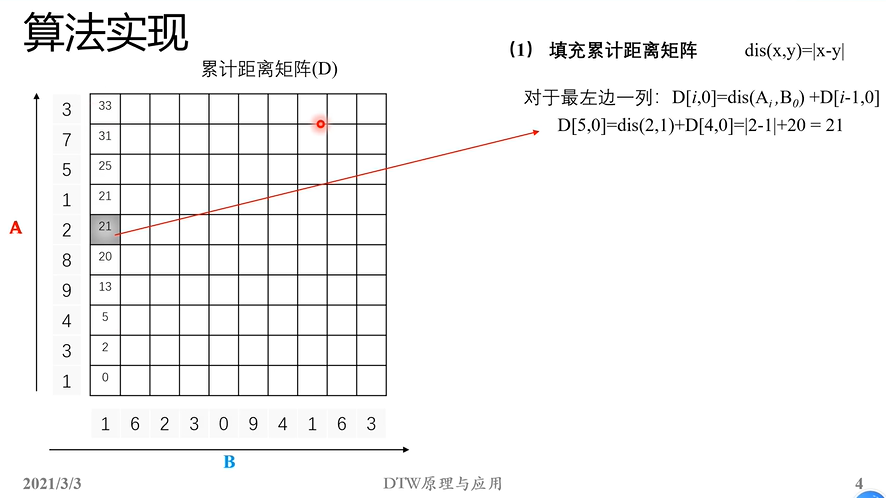
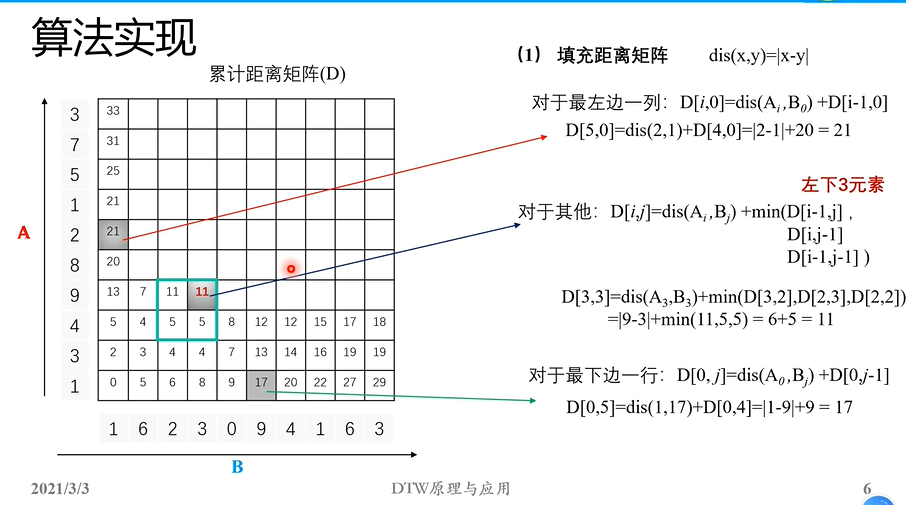
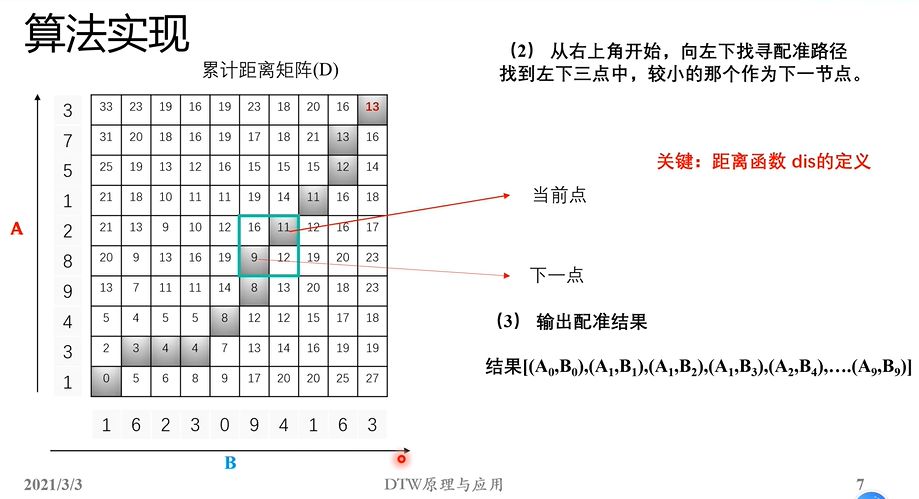
填满了整个累计距离矩阵D后,下一步就是根据距离最小的原则,找到A中元素和B中元素之间的对应关系,也即在矩阵中找一条路径出来。
路径的找法,前面讲过对应完了之后,一定是A中最后一个点对应B中最后一个点,第一个点对应着第一个点。所以路径寻找的起点一定是矩阵右上角的点。从右上角那个点开始,按照距离最近的原则查找下一个点;下一个点的查找方法就是找当前点左下方的三个点(左边一个,下边一个,左下边一个)中的最小值,作为下一个点;(网友:能不能从左下角开始;)。那为何执照左下方的三个点呢,是因为是一步匹配的,每次只能一个一个点来匹配,所以说找的时候,也只能找左下方的三个点。
按照上述找点,直到找到左边;然后这个找的过程中得到的各点连起来,就是所需要的路径。
以上就是DTW算法的过程。下面看下如何用Python实现。
网友:说的好清晰,如果我想从一个长序列中识别出所有和模板序列相似的序列请问有什么思路吗?如果A和B是一个三维的矩阵呢?也就是说要比较两条三维空间的曲线的相似w性;如果是回溯的时候左下发有两个一样的值怎么办呢。应该任意选择其中一个吧;
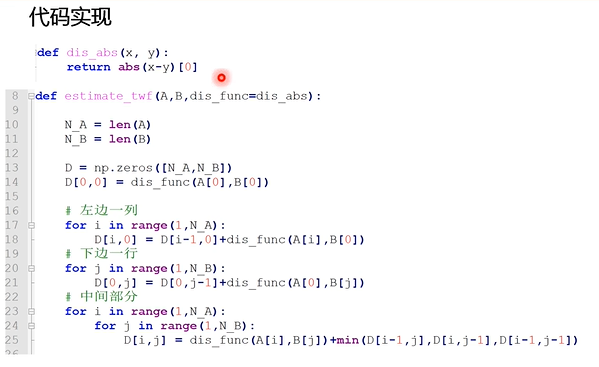
上述代码中,A,B数据的存放格式实际上是[N,D],其中N是样本的数目,D是数据特征的维度,只不过这个例子里面数据样本的特征维度是1;
上述第二个函数代码依次:得到A和B矩阵的长度N_A,N_B,然后计算累计距离矩阵D,应该是个N_A*N_B的矩阵。它左下角元素D[0,0]就是应该就是A[0]和B[0]之间的距离:dis_func(A[0], B[0])。
然后再依次对累计距离矩阵左边的一列、下边的一列和剩余的中间位置进行填充;
这样就能够把累计距离矩阵D算完了。
网友:您好,我想问一下如果是两个不同的坐标系下应该怎么做匹配?映射到同一个hidden space?我个人感觉是可以直接映射匹配到一个坐标系里面。可是Python里不就有dtw的库吗,可以直接调用。
有了累计距离矩阵D就可以实现路径回溯问题了,进而把路径找出来。

找路径时,从右上角开始找。右上角的坐标分别是NA-1,NB-1;count是用来统计最终得到配对点的数量。
d表示把配对点的距离给记录下来;用d=np.zeros(NA,NB) *3来表示;但中间肯定有弯的,所以最大的长度可能会是2倍的(NA,NB)中的最大值,但我们为了保险,所以用了3倍;
path是了列表,其是把匹配点的位置坐标给记录下来。
然后进入while True循环,进行运行操作。
网友:j=0走到最左边了吧,i=0走到最下边。
每个路径以及每个路径对应的距离都求解出来了,放在了d里面。
然后np.sum(d)/count,求得均值。这个均值实际上就衡量了两个序列之间的距离,然后返回均值(实际是两个序列之间的距离)和路径D。因为路径是从后往前找的,所以我们返回的时候,应该是从前往后返回也就是path[::-1];然后D是累计距离矩阵所以也一块返回 。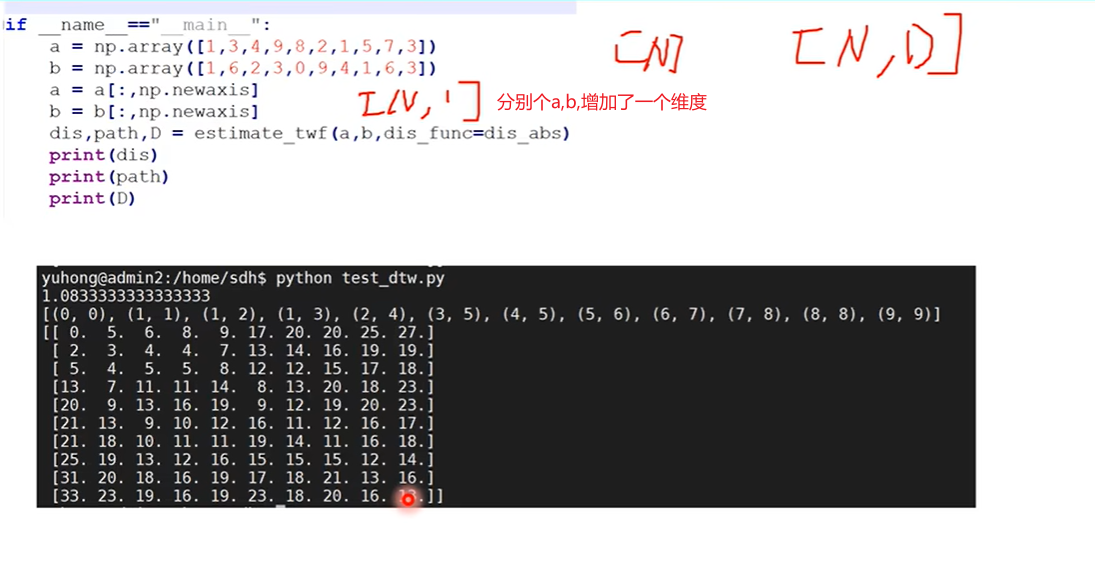
可看到上图打印的结果和前面运算的结果一致。
增不增加维度,都好像没啥影响吧,不解;深度学习里,样本数通常不止一个,所以是二维的[Batchsize,feature dim]。由于这里每个序列单元只有一个数字,所以f dim = 1。如果a和b是三维的呢?把dis改为空间点的距离公式就可以吗?

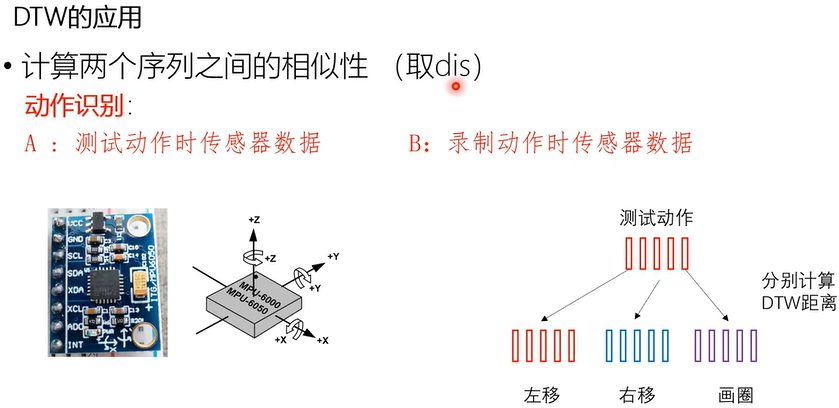
上图左部的一个动作识别传感器。MPU-6050传感器,这个传感器可以计算你运动时,在X,Y,Z三个方向的加速度和X,Y,Z三个轴转动的角速度变化,然后就可以用这个传感器实现动作识别的功能。
比如上图右部把装有传感器的设备,左移、右移、画圈等动作过程中的传感器数据记录下来;然后进行测试动作,传感器中会传来一系列数值,然后记录下来。因为三个轴的加速度、角速度各有3个,所以共六个,是个6维度的数据。然后把测试动作的序列和保存好的动作序列分别进行DTW距离的匹配,然后计算DTW的距离并找到距离最近的那个动作,作为最终的输出,也就实现了动作记录和识别的功能。这样就比较简单。这是一种应用。也就是我把DTW计算过后,取得了dist,然后用dist评估两个序列之间的相似性,然后做识别。此例为取距离的应用。
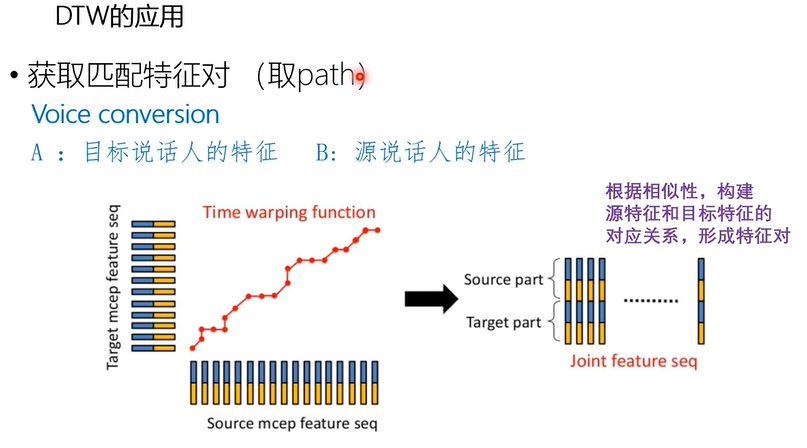
上图为DTW在声音转换功能方面的一个应用。如上图需要把B的语音特征转换成A的语音特征。
转换过程就是要构造一个转换函数,这个函数需要把源说话人B的声音特征,转换成目标说话人A的声音特征;
那么就要先把A,B的声音特征配成对,配成对后才能构造转换函数;这个配对过程则可以利用DTW算法来实现;如山图左部所示蓝黄相间的声音序列,配对并通过DTW计算,构造他们帧与帧之间的对应关系,进而构造特征对,有了特征对之后就可以利用特征对进行计算转换函数,来实现声音的转化。此应用为取匹配的特征对。
网友:心电图的GAN好像也可以用这个,相当于augmentation。
但是应注意到,参与匹配的两个序列往往不会有相同的属性和长度。如下例所示: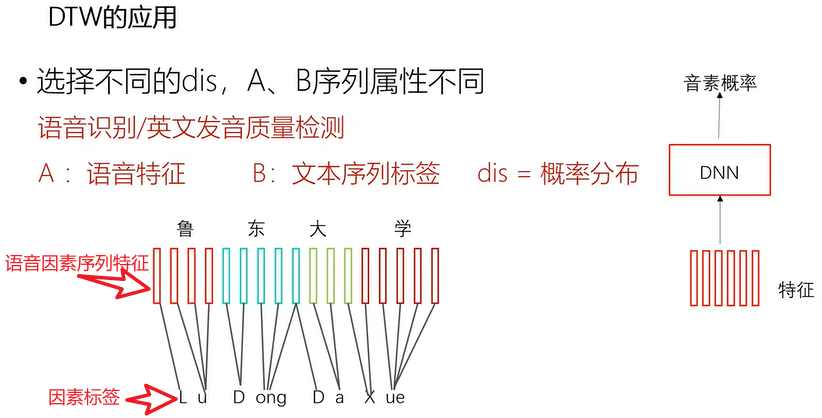
如上图所示,语音因素序列特征和因素标签长度并不一样;现在要把语音特征A匹配到因素标签B(拼音)上,要让他们之间对齐,那么他们之间如何对齐呢?
这个也和我们前面讲的意义,直接算距离就行了;就算语音和语音的文本标签之间的距离就行了,这个距离的算法就不能用上述讲解的欧式距离等来计算了,我们就需要提前训练一个深度神经网络的分类器,这个分类器输入的是特征,输出的是音素的概率;这时的dist不再是一个具体的数值了,而是概率值;利用概率值来作为距离;那么这样有了两个序列特征了、有了距离了,那么就可以对他们匹配了,匹配完了后,根据前面讲的匹配原则,这个是单向匹配的,自然的就看到Lu这个拼音对应的是哪些特征,...,Xue对应的是哪些特征。这个过程在语音处理里面有个对应的专属名词叫做强制对齐。
上述强制对齐完后的应用一般有一下几种,我们现在常用的英语发音纠正软件,比如英语流利说、自动配字幕的软件(随着你的说话,不同的字幕就会产生不同的颜色变化,e.g.歌词等随着你唱歌,歌词颜色变化;),实际上都是用这样的算法实现的;比如说我们要实现发音标准的评估软件,首先你说一段话,提取特征,然后标签你也知道了,利用DTW算法把标签和特征强制的匹配上,匹配之后,就可以知道你说的具体的字词的匹配距离是多少,比如知道阿上图中的Lu对应的匹配语音距离是多少,Dong的是多少,Da是多少,Xue又是多少。然后就可以根据匹配的距离来评估你发音的好坏。比如说距离比较近,那么发音就比较标准,距离远则反之。这样就可以做一个发音纠正。
from fastdtw import fastdtw from scipy.spatial.distance import euclidean x = np.array([1, 2, 3, 3, 7]) y = np.array([1, 2, 2, 2, 2, 2, 2, 4]) distance, path = fastdtw(x, y, dist=euclidean) print(distance) print(path) # 5.0 # [(0, 0), (1, 1), (1, 2), (1, 3), (1, 4), (2, 5), (3, 6), (4, 7)]
此外可参考:
https://www.jianshu.com/p/dad0324bf241
面临的问题
当数据在时间线上不对齐的时候,使用传统的匹配方法,是无法使用传统的全局匹配度量法的。
DTW算法简介
两个人分别说了同一个单词,但是由于语速、语气、语调等等各不相同,会导致采样得到的数据无法对齐。但是两段语音采样的第一个采样值和最后一个采样值肯定是两两对应的。
给出两个序列:

Warping通常采用动态规划算法。为了对齐这两个序列,我们需要构造一个n x m的矩阵网格,矩阵元素(i, j)表示qi和cj两个点的距离d(qi, cj),一般采用欧式距离,d(qi, cj)= (qi-cj)2(也可以理解为失真度)。每一个矩阵元素(i, j)表示点qi和cj的对齐。
DP(dynamic programming)算法可以归结为寻找一条通过此网格中若干格点的路径,路径通过的格点即为两个序列进行计算的对齐的点。
有三个性质:
1)边界条件:w1=(1, 1)和wK=(m, n)。两个人分别说了同一个单词,但是由于语速、语气、语调等等各不相同,会导致采样得到的数据无法对齐。但是两段语音采样的第一个采样值和最后一个采样值肯定是两两对应的。因此所选的路径必定是从左下角出发,在右上角结束。
2)连续性:如果wk-1= (a', b'),那么对于路径的下一个点wk=(a, b)需要满足 (a-a') <=1和 (b-b') <=1。也就是不可能跨过某个点去匹配,只能和自己相邻的点对齐。这样可以保证Q和C中的每个坐标都在W中出现。
3)单调性:如果wk-1= (a', b'),那么对于路径的下一个点wk=(a, b)需要满足0<=(a-a’)和0<= (b-b’)。这限制W上面的点必须是随着时间单调进行的。以保证图B中的虚线不会相交。
由连续性和单调性可知,每次格点(i, j)前进方向只有三种:(i+1, j),(i, j+1) 或 (i+1, j+1)。我们的目的是使得下面的规整代价最小的路径:

分母中的K主要是用来对不同的长度的规整路径做补偿。
这里我们定义一个累加距离(cumulative distances)。从(0, 0)点开始匹配这两个序列Q和C,每到一个点,之前所有的点计算的距离都会累加。到达终点(n, m)后,这个累积距离就是我们上面说的最后的总的距离,也就是序列Q和C的相似度。
示例:
对于两个序列:
X:3,5,6,7,7,1
Y:3,6,6,7,8,1,1
有距离矩阵:
X和Y的距离矩阵:
| X/Y | 3 | 6 | 6 | 7 | 8 | 1 | 1 |
|---|---|---|---|---|---|---|---|
| 3 | 0 | 3 | 3 | 4 | 5 | 2 | 2 |
| 5 | 2 | 1 | 1 | 2 | 3 | 4 | 4 |
| 6 | 3 | 0 | 0 | 1 | 2 | 5 | 5 |
| 7 | 4 | 1 | 1 | 0 | 1 | 6 | 6 |
| 7 | 4 | 1 | 1 | 0 | 1 | 6 | 6 |
| 1 | 2 | 5 | 5 | 6 | 7 | 0 | 0 |
然后根据距离矩阵生成1损失矩阵(Cost Matrix)或者叫累积距离矩阵 McMc,其计算方法如下:
-
第一行第一列元素为 MM 的第一行第一列元素,在这里就是0;
-
其他位置的元素 (Mc(i,j)Mc(i,j))的值则需要逐步计算,具体值的计算方法为 Mc(i,j)=Min(Mc(i−1,j−1),Mc(i−1,j),Mc(i,j−1))+M(i,j)Mc(i,j)=Min(Mc(i−1,j−1),Mc(i−1,j),Mc(i,j−1))+M(i,j),得到的McMc如下:
| X/Y | 3 | 6 | 6 | 7 | 8 | 1 | 1 |
|---|---|---|---|---|---|---|---|
| 3 | 0 | 3 | 6 | 10 | 15 | 17 | 19 |
| 5 | 2 | 1 | 2 | 4 | 7 | 11 | 15 |
| 6 | 5 | 1 | 1 | 2 | 4 | 9 | 14 |
| 7 | 9 | 2 | 2 | 1 | 2 | 8 | 14 |
| 7 | 13 | 3 | 3 | 1 | 2 | 8 | 14 |
| 1 | 15 | 8 | 8 | 7 | 8 | 2 | 2 |
DTW要去解决的问题
DTW就是要去解决,普通的欧氏距离,对不对齐的两个序列无法进行相似度对比的问题。解决的方法就是动态规划,但是并没有生成更加多余的点,而是进行了复制。
DTW存在的问题
DTW实质上是通过对轨迹点的复制实现的对轨迹局部的拉伸或者缩放,下图展示地非常清楚:

DTW通过迭代的方式计算轨迹之间的距离(找到图4 b所示的最佳的轨迹),是一个经典的动态规划问题,其算法复杂度是O(m × n),依旧很高。后期必然需要相应的修建策略才能达到好的效果。
虽然没有使用映射,但是由于使用了重复,最终的结果仍然不是严格的metric,无法使用metric的方法!(DTW “loosely” satisfies the triangle inequality. It appears that this observation is not true in general, as on average nearly 30% of all the triplets do not satisfy the triangle inequality.)
“复制“其实就是在重复使用某些点。以此实现了对local time shifting的处理。
没有阈值限制,其最终目的只有找到最好的路径,但是此路径的总距离大小可能会很大。假如不对离群点进行处理,此算法依旧将会对离群点、异常点很敏感。
算法需要第一个点和最后一个点是对应的。
错误示例:
(1)没有设置阈值

此处出现了特定的local time shifting,会导致T2和T3明明是一条轨迹,但是最终出现的结果会是T1和T3的相似度要比T1和T2差很多。而且最终的结果是绝对的,即得到的只有一个绝对的数字,但从这个数字上是无法进一步消除这个误差的。
(2)直接使用的是原有的轨迹点,重复使用,且不会跳过任何一个点,因此对噪声点的抑制并不好。

总结:
DTW方法是欧氏距离方法的改进,只改进了其不能处理local time shifting的问题。没有引入任何阈值参数,因此对时间上的偏移(噪声和离群点)的抑制并不好,且对时间上的偏移的适应性也不好。
优点:使用动态规划的思想,实现了对某些点的重复使用,确保重复使用的点达成的路径最优的,从而较为高效地解决了数据不对齐的问题。
缺点:还是无法处理离群点、异常点,对于噪声的抑制没有进行处理。虽然能够处理local time shifting,但是对时间上的偏移做的也不好。算法也不是metric类型的。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号