运筹学笔记13 两阶段法





引入两个人工变量x4,x5,各自追加到每个等式约束条件中。但是这样强制插入原来的等式约束条件中后,虽然说有单位矩阵了,但是有可能破坏原来的等式约束条件;
也有可能不破坏(如果最后的x4,x5算出来的值都为0的话),如果有一个是正的大于零的,那么就破坏了原来的等式约束条件,也即原来的等式约束条件就不应该成立,或原来的
线性规划问题是没有可行解的,是不可行的。。
这样就引入了人工变量了,有一个单位矩阵了。但是也有可能破环原来的约束条件,所以要施加一个惩罚,在两阶段法中引入的惩罚是一个新的目标函数z1,其是新引入的人工变量的和,因为x4,x5是大于等于零的,所以二者之和的z1也是>=0的,也即是z1这个目标函数值的下届是0;当然z1求最小值的话,也有可能取0;如果z1为0的话,那么x4,x5就被迫只能是0;那么二者的引入就没有任何破坏作用。
引入目标函数的目的就是求把人工变量对等式约束条件的破坏作用,进行惩罚,采用新的目标函数的方式来进行惩罚的。这种方式和大M法似乎不同,其实是一样的。
除了原有的目标函数为,新引进的目标函数为z1,这就构成了辅助线性规划问题LPe。
下面就利用找到的初始可行基,B=(P4,P5)=I2,来继续进行。
此处要注意,写典式的时候,新增的目标函数z1中的x4,x5要用非基变量代替表示;


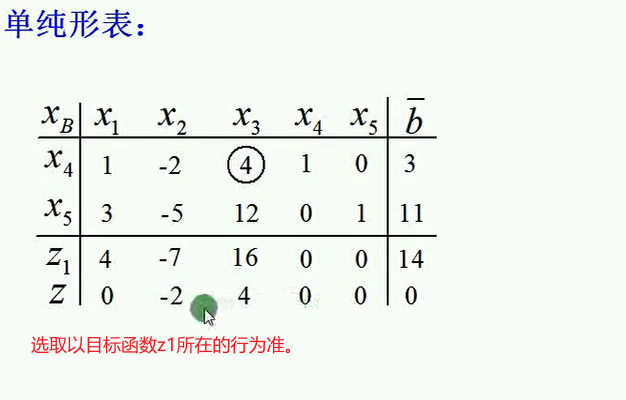
转轴时,原目标函数z所在的行也要参与。
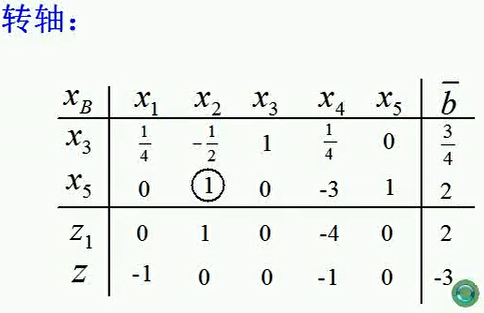


由上图可知,到此步为止,z1所在行的检验数一个时0,一个时-1,没有>0的数值,所以表格就对应着以z1为目标函数的辅助性规划问题的最优解的,
把最优解写出来后得到(0,2,7/4,0,0),两个人工变量全等于0,也即全部惩罚为0了,这就实现了我们最初最好的设想。这就表明原来的约束条件可行的,且同时我们得到的基变量x2,x3对应的基,应该是经过一系列操作得到的原始的初始可行基。所以到此,第一个阶段就完成了。第一个阶段是以z1为目标函数来完成的,但是z这一行目标函数也同时参与了运算,到目前,人工变量已经都惩罚为0了,所以转入第二个阶段。因为x4,x5已经被惩罚为0了,所以把x4,x5所在的列,以及z1这个目标函数所在的行,从这个单纯形表中去掉,因为他们的使命已经完成了。
进而得到了下图所示的缩减了的,变量和目标函数为最原始的线性规划问题LP。此时只需要对下图的表进行最优性的检验,再做进一步的工作。

而也正好赶上了,缩减后的表,此时的检验数正好是-1,我们也就可以直接据此写出最优解和最优值了。
到此,第二个阶段就结束了。这样就利用两阶段法求出来了最开始的LP的最优解了。此处需注意,此题的第二个阶段的
一开始就对应着最优解,所以第二个阶段实际上没有进行;如果在第二个阶段的一开始仍然有正的检验数,也还是需要转轴的。
另外,上图中的最后一行写错了,应该是最优值是-3.




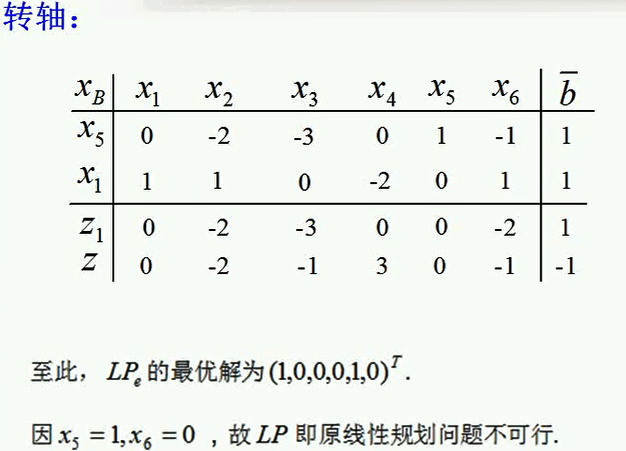
此题,因为引入的两个人工变量x5=1,x6=0,也即原来LP的等式约束条件,是不应该成立的,矛盾的。从而线性规划问题是不可行的。
这就是人工变量没有被完全惩罚为0,就出现了这种不可行的情况,这个时候还用在往下做吗?不用了,第二个例子也就完成了。
第三个例子如下,要注意下面的这个并不是标准形;
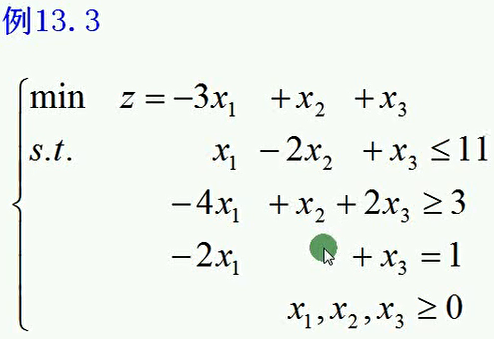



 浙公网安备 33010602011771号
浙公网安备 33010602011771号