运筹学笔记12 大M法



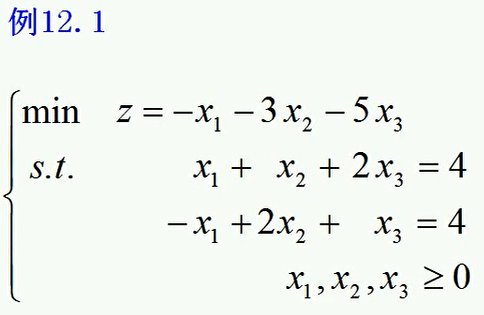

引入M,其中M是一个充分大的正数。由此,目标函数也改变为zM.
如此构造的线性规划问题我们记作LPM,称之为辅助线性规划问题,也即在原来的线性规划问题的基础上,改造了其等式约束条件,然后有对目标函数施加了惩罚项,Mx4,Mx5。
因为M是充分大的正数,所以即便x4,x5很小,只要x4,x5不等于0,这个惩罚项也也会很大的;一旦大M趋于正无穷,那么Mx4,Mx5一块就是正无穷了;而前面的各变量及其系数
的组合也是有限的量;根据一个有限的量加上一个无穷大量结果是无穷大量定理;那么目标函数就是趋于无穷大量,怎么还会取得最小值呢?∴大M叫做惩罚项是有道理的,而且
在理想的状态下,一旦x4,x5取值为零,那么目标函数中就再也没有惩罚项了,目标函数也就有zM还原为z了,同时约束条件x4,x5也就消失了,因为二者此时为零;
这样也就实现了有LPM向原线性规划问题的还原。所以大M法,首先引入大M惩罚项,对人为引入的人工变量施加惩罚,最佳的状态就是把引入的人工变量都惩罚为0,这样不仅等式约束条件没被破坏,目标函数也还原为原来的目标函数了。如果做不到这一步,就说明有些约束条件原来就不可能相等。
我们构造辅助线性规划问题后可看到已经有x4,x5系数组成的单位矩阵了,我们把它取作初始可行基。

进而可以写出典式的等价形式(把基变量和目标函数都用非基变量表示)如下:

进而做出单纯形表:

有了单纯形表,进一步讨论三种情形。
情形1:是否全部的检验数都<=0;很显然此题不是;1肯定是>0的,另外M是充分大的正数所以3M+3,3M+5也都是>=0的。
情形2:正的检验数上面没有正的,才是第二种情况;此题不符合;
显然是第三种情况了,选定枢轴列->元,然后转轴。

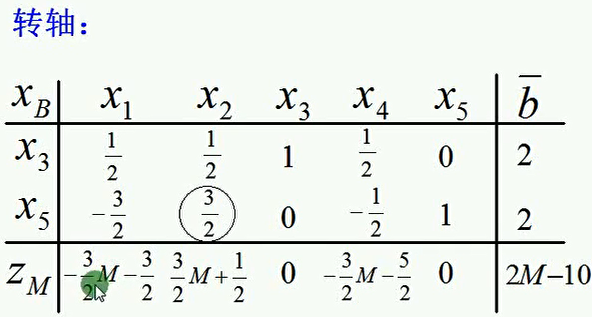
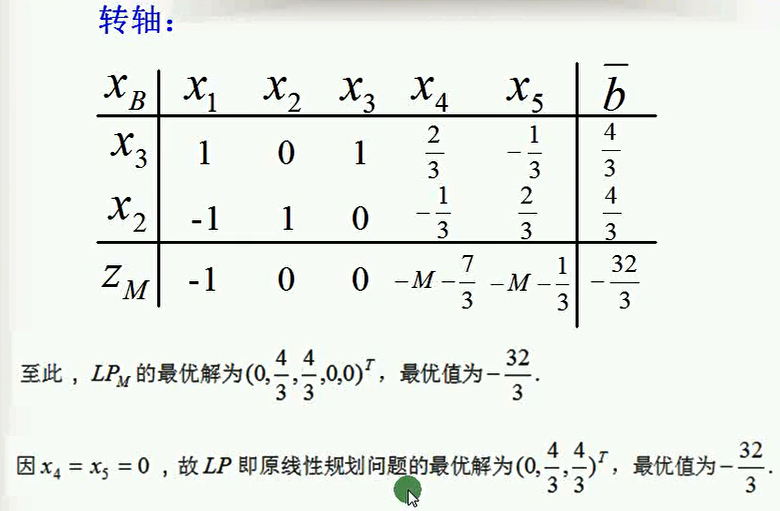
上图得到了辅助线性规划问题的最优解和最优值,但须注意,在辅助线性规划问题中,我们引入了两个人工变量的值,x4,x5,
也可发现在LPM的最优解中两个变量都已经为0了。也即是说,辅助线性规划的人工变量都已经被充分大的大M构造的惩罚项惩罚为0了,也就是说又还原为原来初始的线性规划问题了,所以据此我们就可以得到LP,即原来线性规划问题的最优解和最优值。。。
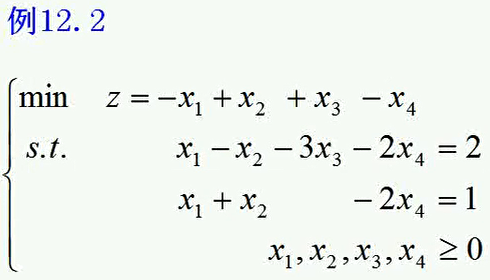




可看到上图中有一个检验数是正的,其所在列上面的值都是<=0,所以是第二种情形,所以LPM无下届。
而之前引入的人工变量x5对应的取值为1,并没有被惩罚为0;另一个非基变量x6作为非基变量已经被惩罚为0了;
也即,因x5=1,x6=0,故原线性规划问题不可行。

练习:
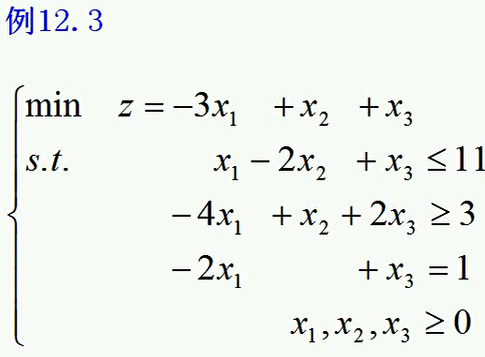



 浙公网安备 33010602011771号
浙公网安备 33010602011771号