运筹学笔记9最优性的检验


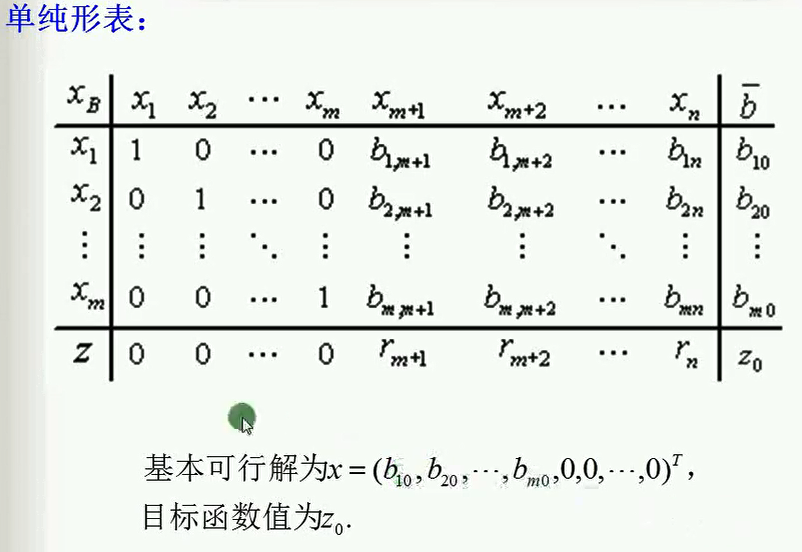
上图中,基本可行解首先是基本解,基本解中非基变量的值全等于零,所以后面n-m个非基变量取值都是零。
基变量的值是表中最后一列,最后一行上面的值。因为取定的基是可行基,所以基本解就是基本可行解了。
基本可行解代入到目标函数里面以后,函数值就是表最右下角的z0。
所以单纯性表给我们的信息很多。
那么基本可行解,作为一个可行解有没有可能是最优解呢?那么就需要检验。



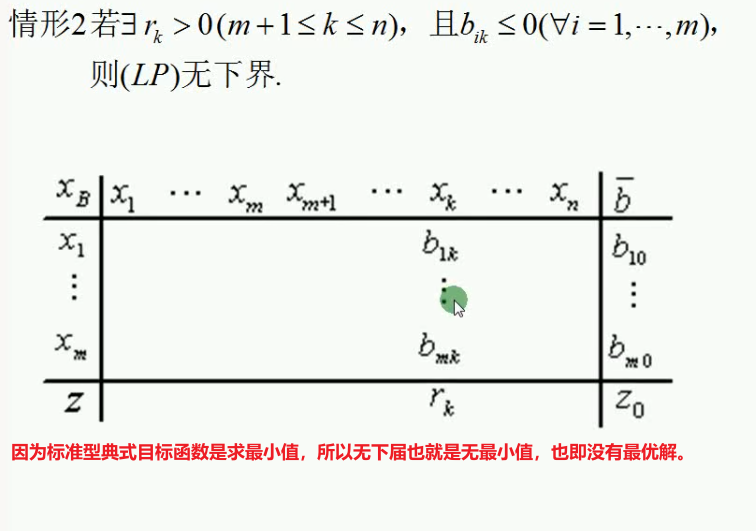
即其所在的列的bik值全部小于等于0.
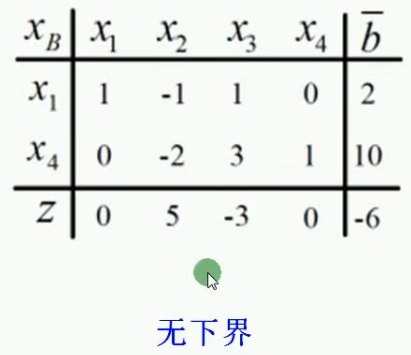

情形3也即时说,检验数有正的,正检验数上面的一列数值中也有正的。
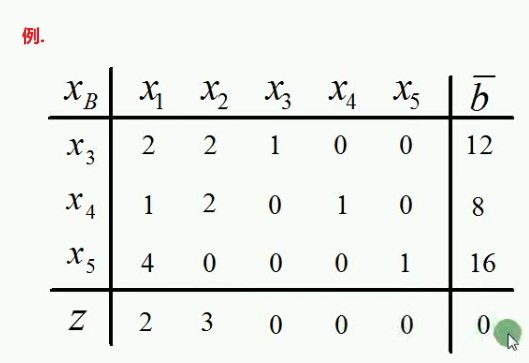
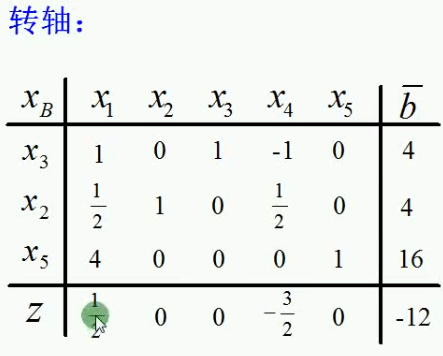
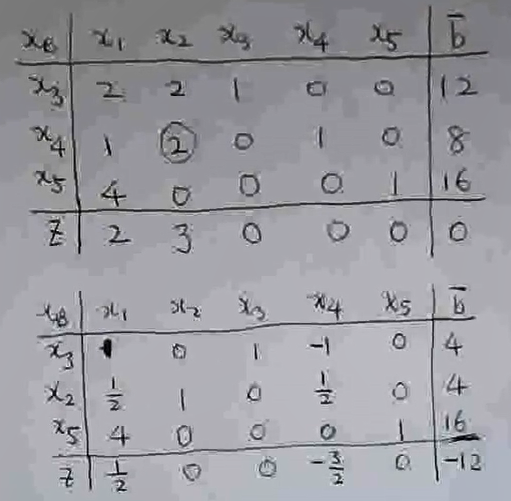
转轴做法:从正的检验数种取一个最大的,把其对应一列的数值中的正数作为分母,算这列数字中的每个数与其对应的bi0数值的比值,找出壁纸最小的那个brk,
然后,以此为中心,进行转轴;假设在所有的比值中,brk/br0是最小的那个。则把第r行对应的基变量xr不再作为基变量,而把brk所对应的k列的xk作为新的基变量。
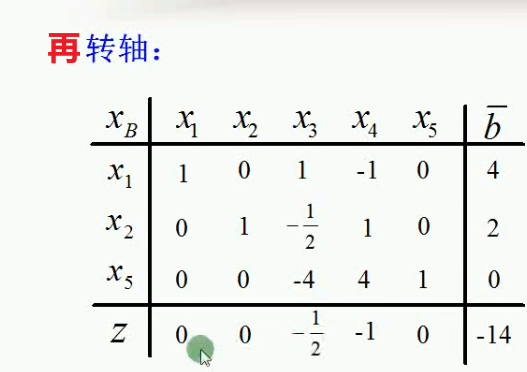
然后进行转轴。转轴后效果如下图所示:






 浙公网安备 33010602011771号
浙公网安备 33010602011771号