运筹学笔记6初始可行基

 

 

 

 

 

 

 

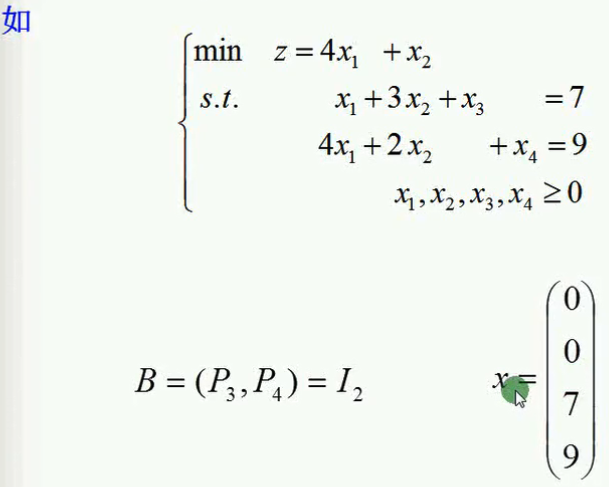
可看到，上图中的线性规划问题已经是一个标准形了；且其等式约束条件中有两个方程，恰好其第三四列构成了一个单位矩阵，是其子矩阵。

我们可把第三列第四列组成的单位矩阵取为基，这个基恰恰就是可行基，那我们的初始可行基也就找到了。这就是第一种类型：约束方程组的

系数矩阵中如果有一个单位矩阵，那么我们把他取为初始可行基，当然它是否是初始可行基，我们可以稍加验证；我们可以求出这个基对应的基本解；

基本解的求法就是让约束方程组中的非基变量都取为零，也即第一个约束等式中的x1,x2都取为零；那就得到x3=7,x=9,同时x1,x2都取作零了，写出来如

上图右下角所示。这个基本解也满足所有变量大于等于0的约束，所以这个基本解同时也是可行解，也即上图右下角这个x向量是一个基本可行解，

其对应的基就是可行基，也就是B=(P3,P4)。