运筹学笔记4线性规划问题的几何特征
也即是从几何上给线性规划问题的概念给一个具体的说明。

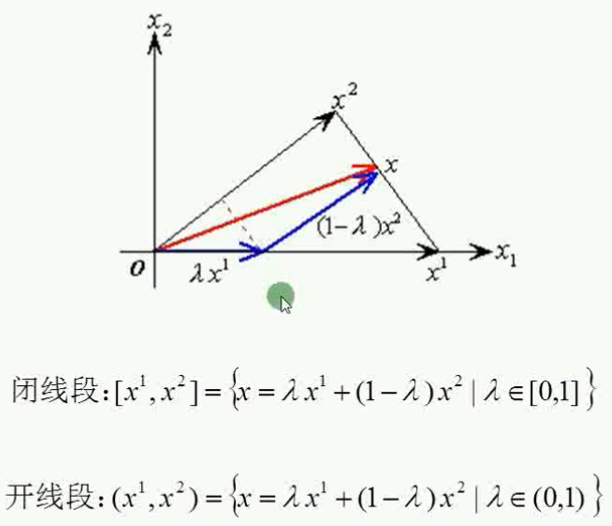
连接x1,x2的线段,如果包括x1,x2端点则称为闭线段,不包括则称为开线段。 数学上表述为,任取线段内部的某一点x,如果能写出/描述出这点x的轨迹或其坐标变化的规律,
就可以。为了做到这一点,我们设想有x1,x2,分别有以x1,x2为终点的向量也有在二者之间任取的一点x为终点的向量,让后把以x为终点的向量,用以x1,x2为终点的向量表示。
如下图,大体做法为,过点x做向量ox2的平行线,在下图的三角形中,两条蓝色和一条红色向量,其中x轴的蓝色向量是ox1向量的一部分,然后用x1,x2表示ox向量,当x1,x2前面的系数lamda在0和1之间变动时,x也就在线段x1x2上来回变动,那么所有x的轨迹也就是闭线段;如果lamda不取0和1那么,就称为开线段。
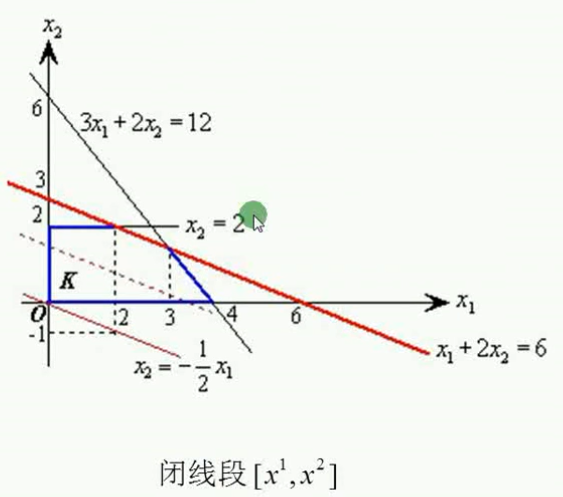
前面讲过一个例子,如下图示,在交点处(2,2)和(3,3/2)处都是最优解,且连接两个点线段之间的任意取值都是最优解;所以闭线段就是以某两个点为端点连接而成的闭合的线段而已。
凸集,如下图中第一个图形,它是一个凸多边形,往外补/顶的多边形,所围成的一个区域/集合,我们称之为凸集。
数学上可这样描述:
在某集合的内部任选两个点,连接这两个点的闭线段仍然示含于这个集合的,我们就称这个集合为凸集。
所以,有这样的若干条直线,围成的凸多边形区域一定示凸集。


大家注意:圆面是不是凸集?肯定是的。因为在其内部任选两点。。。。
但是,圆并不是凸集,因为,在圆边上任选两个点,很显然并不完全在圆上。同理球面也不是。但是,球体是凸集。
顶点:就是不在任意两个点连线的内部(不含端点)的点;如下图的五个顶点(已标出);
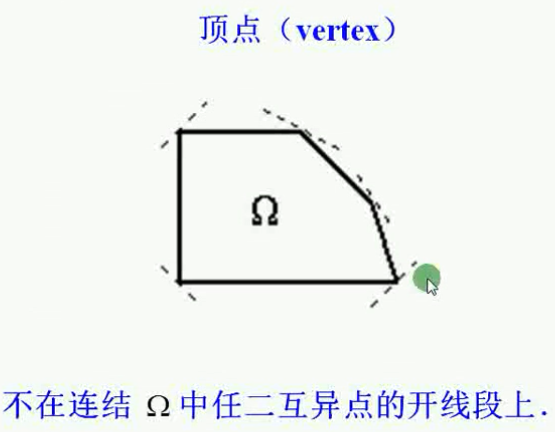
上图看得到,凸多边形(正好构成一个凸集)的顶点,恰好就是凸多边形构成的凸集的顶点。 那么,圆面是一个凸集,那么圆面有没有顶点呢?有的,圆面的边界就是它的顶点。
同理,球体的顶点示球体的表面。所以不要以为,凸集的顶点总是凸多边形的顶点,这个不一定。因为这个凸集本身就不一定示多边形区域。各种各样的凸集,有各种各样的顶点,
就像此处的圆面和球体他们也有自己的顶点。自己理解的:也即凸集顶点可以是面或曲线。
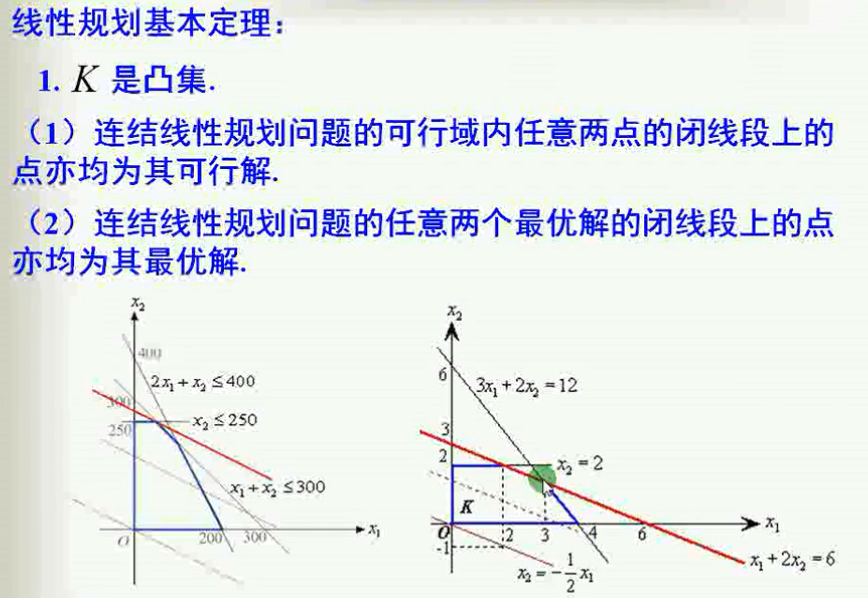
线性规划基本定理:
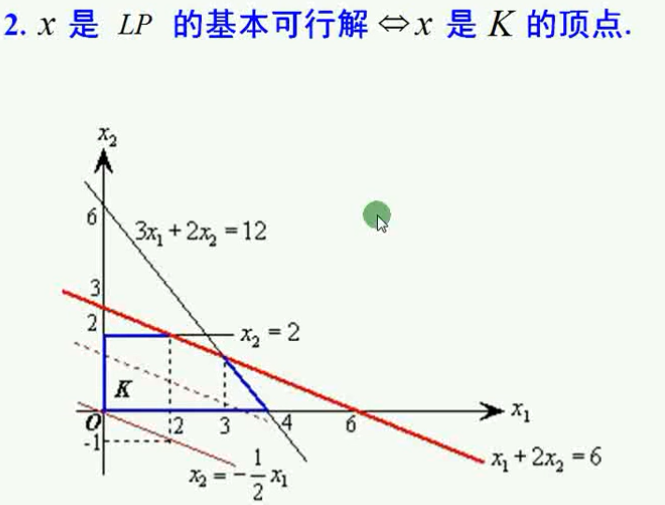
1. K是凸集;K是可行域(线性规划问题的可行域);也即说线性规划问题的可行域是凸集;可看下图,我们看过的例子,这个例子有唯一最优解,他的可行域是蓝色线段围起来的,很显然是凸集;
LP的基本可行解与其可行域的顶点是一一对应的。
如下图的坐标图中可行域有5个顶点,所以其对应的线性规划问题,就有5个基本可行解;因为一一对应,不多不少。
基本可行解理解起来可能没那么直观,有点抽象,没那么容易理解。但是可行域的顶点,就很直接了,就是几何上的一个点。
也即可行域的顶点,就决定了它的基本可行解,二者是一一对应的。
若那个可行域不是空集,那么它至少有一个顶点。空集的话,就没有了。
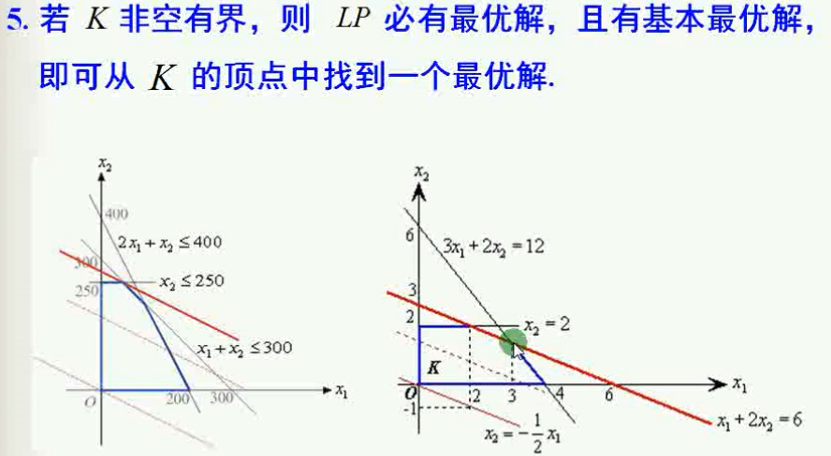
比如,之前学过的例子,是目标函数无界的例子,虽然其可行域也是无界的,但其并不是空集;无界和空集不是一回事。也可看到,其有两个顶点,也不是空集;所以结论正确;
如果可行域是空集,那么就没有顶点了,如下图右下角图例。


一个可行域的顶点,最多有Cnm个,n个变量,m个约束条件,系数矩阵中,从n列中取m列,可以构造一个基,也就是最大可能基的数目,当然不一定有这么多,但这是上限 。
基本可行解的数目肯定不会超过上限,但是也没办法从最多这么多个基本可行解中通过枚举/穷举的方法,一一比较优劣,来找到最优解呢?太慢了!

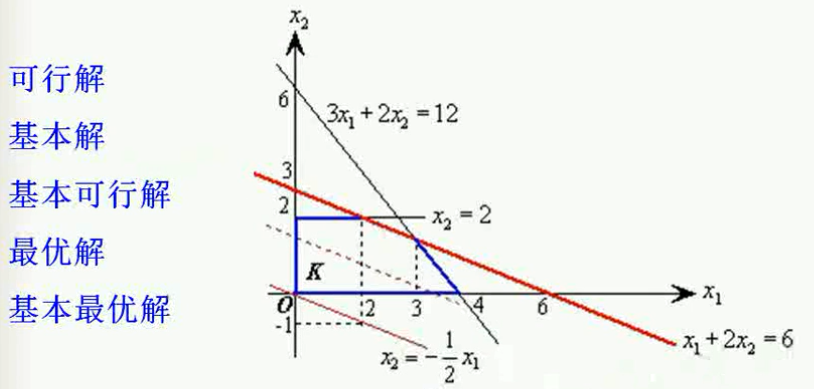
上图中的五个解,能不能从图上一步到位的指出来呢? 如果能指出来那么就很具体了,不会虚无缥缈了。以前面所学的第二个例子,
可知道可行解是可行域的顶点,以及闭合区域内的任何一点都对应这可行解,很直观;
基本可行解对应着可行域的顶点,上图中坐标图中可行域有5个顶点,所以基本可行解就是这5个,别无其他的了。
最优解则是可行区域中红线段上的所有点,有无穷多个。
基本最优解只有两个,也就是可行区域中红线段上的两个端点(也是可行域的两个顶点);它们不仅是最优解,而且是基本最优解。
还有一个基本解没有指出它的位置,那么能否从可行域上指出其在哪呢?这个很难指出来。因为我们前面知道,基本解和可行解没有必然的联系,基本解不一定是可行解,
可行解也不一定是基本解;也即可行解不已经是基本解了,那么你怎么能从可行域中指出哪些基本解呢?但是我们可以找出一些特殊的,叫做基本可行解的基本解,因为他们只有5个顶点对应的才是。但是一般的基本解我们是无法找出来的,因为它连可行解都未必是。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号