隐式曲线曲面与梯度、三角形与重心坐标

目前的图形学研究都绕不开几何图元，其中个人学习中比较难以理解的是隐式曲线和曲面，与之对应的偏导、梯度等几何信息，以及与模型表示最为密切的三角形，因此写下此篇总结，供复习回顾。

隐式曲线曲面

2D曲线最符合直觉的定义可以是：在一张纸上一笔所画出的一条线，而这条线可以表示为一系列点的集合。对于一般情形，用一个方程可以描述任意二维实曲线：

\[f(x,y)=0 \]

由于这条曲线是在方程中隐式定义的，因此也称为隐式曲线。

常见的隐式曲线有：

隐式直线：

\[Ax+By+C=0 \]

隐式二次曲线：

\[Ax^2+Bxy+Cy^2+Dx+Ey+F=0 \]

如隐式椭圆：

\[f(\textbf{p})={(x-x_c)^2\over a^2}+{(y-y_c)^2\over b^2}-1=0 \]

3D隐式曲面与2D隐式曲线类似，可用隐函数

\[f(x,y,z)=0 \]

定义3D隐式曲面，解集即为曲面上所有点的集合，我们可以通过隐函数判断点是否在面上，但大多数时候我们无法显化其表达式，即无法显式构造位于面上的点。

为方便表示，记 \(\textbf{p}=(x,y,z)\) ，则

\[f(\textbf{p})=0 \]

常见的隐式曲面：

隐式平面：已知平面包含点 \(a\) ，且法向量为 \(\textbf{n}\) ，则平面方程为

\[(p-a)\cdot\textbf{n}=0 \]

3D隐式二次曲面如椭球面：

\[f(\textbf{p})={(x-x_c)^2\over a^2}+{(y-y_c)^2\over b^2}+{(z-z_c)^2\over c^2}-1=0 \]

由方程组定义的3D隐式曲线 (曲面的交线)：

\[\left\{ \begin{aligned} f(\textbf{p})&=0\\ g(\textbf{p})&=0 \end{aligned} \right. \]

梯度

梯度是一个重要的度量，在几何领域，除了用梯度描述变化之外，梯度还经常用于求法线等操作。

对于一维的情况，我们可以用极限定义导数为切线斜率。而一个二维函数并不能做类似一维情况下的极限运算，因为对于给定的 \(x\) ，\(f\) 的变化方式多种多样，而如果我们把 \(y\) 视为常数，则可以定义一个类似导数概念，这就是偏导数 (Partial Derivatives)：

\[{\partial f\over\partial x}=\lim_{\Delta x\rightarrow0}{f(x+\Delta x,y)-f(x,y)\over\Delta x} \]

如果把函数值当成第三维，那么可以表示为一个高度场，此时 \((x,y,f(x,y))\) 是一个三维表面。在 \(xOy\) 平面上任意指定一个方向，我们都可以定义一个该表面的导数，该导数值是沿这样一个方向的导数，这个方向在 \(xOy\) 平面的投影为我们所指定的方向，这就是方向导数 (Directional Derivatives)。对应回二维的情况，这里实质上是对导数做了推广。对 \(x\)求导，实际上是求沿 \(x\)​ 方向的函数变化率，既然是对方向求导，自然可以推广到沿任意方向求导，也就是方向导数。 (但其实有细微区别，通常讨论的可求导或偏导，指的是沿轴向双向均可导且导数值均相同)

设 \(l\)​ 是 \(xOy\) 平面上以 \(P_0(x_0,y_0)\) 为始点的一条射线， \(e_l=(\cos\alpha,\cos\beta)\) 是与 \(l\) 同方向的单位向量 (方向余弦表示)，射线 \(l\)​ 的参数方程为

\[\left\{ \begin{aligned} x&=x_0+t\cos\alpha\\ y&=y_0+t\cos\beta \end{aligned} \right. \]

则方向导数可定义为

\[\left.{\partial f\over\partial l}\right|_{(x_0,y_0)}=\lim_{t\rightarrow0^+}{f(x_0+t\cos\alpha,y_0+t\cos\beta)-f(x_0,y_0)\over t} \]

在可微条件下，有

\[\begin{aligned} &f(x_0+\Delta x,y_0+\Delta y)-f(x_0,y_0)\\ =&f_x(x_0,y_0)\Delta x+f_y(x_0,y_0)\Delta y+o\left(\sqrt{(\Delta x)^2+(\Delta y)^2} \right)\\ =&f_x(x_0,y_0)\cos\alpha+f_y(x_0,y_0)\cos\beta+o\left(t\right) \end{aligned} \]

故

\[\left.{\partial f\over\partial l}\right|_{(x_0,y_0)}=f_x(x_0,y_0)\cos\alpha+f_y(x_0,y_0)\cos\beta \]

基于方向导数可以定义梯度。梯度 (Gradients)是一个向量，它指示的就是这样一个方向：从当前点出发在曲线上运动时，沿该方向运动，高度爬升得最快，变化率最快，或者说，方向导数最大。可以定义梯度

\[\mathrm{grad}f(x_0,y_0)=\nabla f(x_0,y_0)=f_x'\ \textbf{i}+f_y'\ \textbf{j} \]

其中， \(\nabla={\partial\over\partial x}\ \textbf{i}+{\partial\over\partial y}\ \textbf{j}\) 为向量微分算子Nabla。

根据方向导数的定义可知，

\[\left.{\partial f\over\partial l}\right|_{(x_0,y_0)}=(f_x',f_y')\cdot e_l=\left|\mathrm{grad}f(x_0,y_0)\right|\cos\theta \]

由于射线的方向向量是单位向量，因此最终方向导数可以表示为上式，其中， \(\theta\)​ 是射线方向向量与梯度方向的夹角。当射线方向与梯度方向相同时，方向导数取得最大值，且最大值为梯度的模。

若取平面 \(z=c\) 截该高度场，可得一等值线

\[\left\{ \begin{aligned} z&=f(x,y)\\ z&=c \end{aligned} \right. \]

对应隐式曲线 \(f(x,y)=c\)​ ，改写为参数形式

\[\left\{ \begin{aligned} x&=x\\ y&=y(x) \end{aligned} \right. \]

隐函数两边对 \(x\) 求偏导可得，

\[f_x(x,y)=f_x(x,y(x))=f_x'+f_y'\ y_x'=(f_x',f_y')\cdot(1,y_x')=0 \]

对比定义可知，上式点积为0即表明梯度与切向量垂直。

特别地，令 \(c=0\)​ 即原曲线，也即，曲线法向量可用梯度方法求，且有

\[\nabla f(x,y)=({\partial f\over\partial x},{\partial f\over\partial y}) \]

类似地，3D隐式曲面的法线为

\[\textbf{n}=\nabla f(\textbf{p})=\left({\partial f\over\partial x},{\partial f\over\partial y},{\partial f\over\partial z} \right) \]

同样地，梯度法所求的法线方向指向的是 \(f(\textbf{p})>0\) 的区域。

参数曲线曲面

有时使用参数方式定义的隐式曲线曲面会更便于计算，同时，参数形式给出了一种构造点的方法。

2D参数曲线通常定义为

\[\left\{ \begin{aligned} x&=g(t) \\ y&=h(t) \end{aligned} \right. \]

如圆

\[\left\{ \begin{aligned} x&=R\cos\theta\\ y&=R\sin\theta \end{aligned} \right. \]

3D参数曲线通常定义为

\[\left\{ \begin{aligned} x&=f(t)\\ y&=g(t)\\ z&=h(t) \end{aligned} \right. \]

如螺线

\[\left\{ \begin{aligned} x&=\cos t\\ y&=\sin t\\ z&= t \end{aligned} \right. \]

3D参数曲面通常定义为

\[\left\{ \begin{aligned} x&=f(u,v)\\ y&=g(u,v)\\ z&=h(u,v) \end{aligned} \right. \]

如球面

\[\left\{ \begin{aligned} x&=R\cos\phi\sin\theta\\ y&=R\sin\phi\sin\theta\\ z&=R\cos\theta \end{aligned} \right. \]

三角形与重心坐标

三角形是最基本的图元。由于通常我们只拥有给定的三角形的顶点处的信息，在图形计算中，需要插值以生成可平滑覆盖的像素信息。而三角插值依赖最多的是重心坐标。

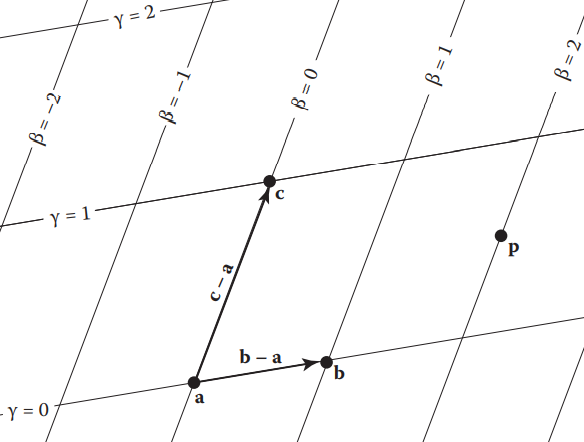
重心坐标 (Barycentric Coordinates)是一个非标准正交的坐标系，其以三角形的一个顶点为坐标原点，以过该点的两边为坐标轴。在三角形所在平面内的任意一点 \(\textbf{p}\) 均可表示为

\[\textbf{p}=\textbf{a}+\beta(\textbf{b}-\textbf{a})+\gamma(\textbf{c}-\textbf{a}) \]

令 \(\alpha=1-\beta-\gamma\) ，整理得一个对称表达的形式

\[\textbf{p}=\alpha\textbf{a}+\beta\textbf{b}+\gamma\textbf{c} \]

则 \((\alpha,\beta,\gamma)\) 称为点 \(\textbf{p}\) 的重心坐标。

利用重心坐标可快速判断点与三角形的位置关系：

• 若坐标分量均位于 \((0,1)\) ，则点在三角形内
• 若坐标分量恰有一个为0，且其余两个均位于 \((0,1)\) ，则点在三角形上
• 若坐标分量有两个为0，则点与三角形顶点重合
• 除此之外，点在三角形外

由于重心坐标的表达式已给出，则可以得到一个关于坐标的方程组，直接求解即可得到重心坐标。但这种方法没有将其几何意义融入计算。

对于重心坐标的一个理解是：坐标的分量值对应该顶点到其对边的有向比例距离 (Signed Scaled Distance)。

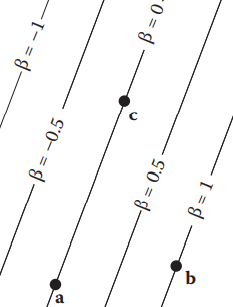
利用之前隐式曲线的知识，对于边 \(ac\)​ ，设其对应隐函数为 \(f(x,y)=0\)​ (这里以二维情况讨论，而其结论可以几乎完全推广到三维情况，只需添加一维坐标即可)，而对于函数 \(d=kf(x,y)\)​ ，其表示的正是平面内的点到边 \(ac\) 有向比例距离，对比重心坐标可知，我们只需要找到一个 \(k\) ，使得 \(kf(x_b,y_b)=1\)​ ，因此我们得以计算重心坐标

\[\beta={f_{ac}(x,y)\over f_{ac}(x_b,y_b)} \]

代入两点坐标，以直线的一般式表示则有

\[\beta={(y_a-y_c)x+(x_c-x_a)y+x_ay_c-x_cy_a\over(y_a-y_c)x_b+(x_c-x_a)y_b+x_ay_c-x_cy_a} \]

同理可得 \(\gamma\) 的表达式，再由 \(\alpha=1-\beta-\gamma\) 即可计算重心坐标。

另一种理解重心坐标的方式是面积法。同样考虑边 \(ac\) ，以之为底的三角形，以同样的 \(\beta\) 为高时，三角形的面积不变，且当 \(\beta=1\) 时，面积为整个三角形的面积，即

\[\beta={A_b\over A} \]

在允许面积带有方向时，该方法也可以表示面内所有的点。又由叉积可得三角形法线和面积

\[\textbf{n}=(b-a)\times(c-a)\\ A={1\over2}||\textbf{n}|| \]

这个面积并非有向面积，所以并不能直接用于面积法求重心坐标。但可以观察到，当三角形的三个顶点绕序不同时，其有向面积的符号也是不同的。因此我们定义

\[\textbf{n}_a=(c-b)\times(p-b) \]

对应由点p、b、c组成的三角形，若p、a均位于bc的一侧，则叉积方向一致，反之则反。又因为所有点均在同一平面内，因此， \(\textbf{n}\) 和 \(\textbf{n}_a\) 平行。那么，

\[\alpha={A_{signed,a}\over A_{signed}}={{1\over2}||\textbf{n}_{a}||\cdot signed(\textbf{n}_a)\over{1\over2}||\textbf{n}||\cdot signed(\textbf{n})}={||\textbf{n}||\ ||\textbf{n}_{a}||\cdot \left<\textbf{n},\textbf{n}_a\right>\over||\textbf{n}||\ ||\textbf{n}||\cdot \left<\textbf{n},\textbf{n}\right>} ={\textbf{n}\cdot\textbf{n}_a\over\textbf{n}\cdot\textbf{n}} \]

推广到3D情况，此时我们假设涉及的点均为三维空间中的点，上述规则仍然成立。

参考

Fundamental of Computer Graphics 4th Edition, Chapter 2.