自制操作系统Antz(15)——实现启动界面

AntzScript

🎓 The language executed in the Antz system.

本节不涉及OS底层内容，只是关于图片放大显示时效果处理的。

Antz系统更新地址

Antz项目地址

真机启动效果

图片来源:phodal/daily

(orz左上角是在处理原图时自己签的名)

为了节省镜像空间，我将图片从2000乘800左右图片压缩为108乘60的24色大小的图片，计算为RGB值之后也有近6400左右像素点。但是要将它写入显存，展现在用户眼中，效果表明是很差的，我们的分辨率为1080x768，数十倍于这张图片。

为了解决显示效果的问题，这里有两种解决方法。

---

一. 像素点区域化

这个方法是我自己起的名字，大致意思也如标题所示，就是将一个本来应该显示在(x1,y1)位置的像素点区域化显示，将其RGB值覆盖在(x1,y1)至(x1+x,y1+y)的这片区域。这个方法实现起来非常简单，但是效果极差，最后显示出来的效果就好像是我的世界中的超大像素点效果。

图示大概如这样:

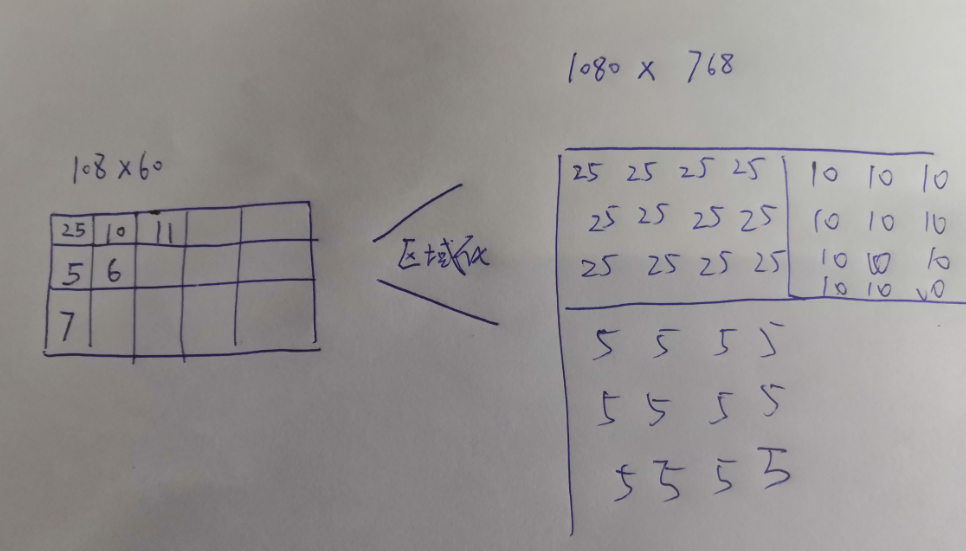
附上简单实现。

void to_show(){
int i, x, y ;
int k ;
k = 0 ;
for (y = 0; y < 60; y++) {
for (x = 0; x < 108; x++){
// 在(x*10,y*13)至(x*10+10,y*13+13)这片区域填充RGB值bmp[k]
print_image(x*10,y*13,x*10+10,y*13+13,bmp[k]);
k++;
}
}
}

在虚拟机中效果如下。

二. 双线性插值

在使用第一种粗略暴力的方式实现启动动画之后，第二天的数字图像处理课程中，听到老师讲matlab中的图片放大缩小函数的原理，了解了双线性插值这个算法，于是想到用这个方法来重新实现启动界面。

双线性插值的基本原理是，假设源图像大小为MxN，目标图像为AxB。那么两幅图像的边长比分别为：M/A和N/B。这两个比例值一般是浮点数。目标图像的第（i,j）个像素点（i行j列）可以通过边长比对应回源图像。其对应坐标为（im/a,jn/b）。显然，这个对应坐标一般来说不是整数，而非整数的坐标是无法在图像这种离散数据上使用的。双线性插值通过寻找距离这个对应坐标最近的四个像素点，来计算该点的值（灰度值或者RGB值）。

其实可以理解为通过其周围的四个点，中和出这片区域中的其他点。

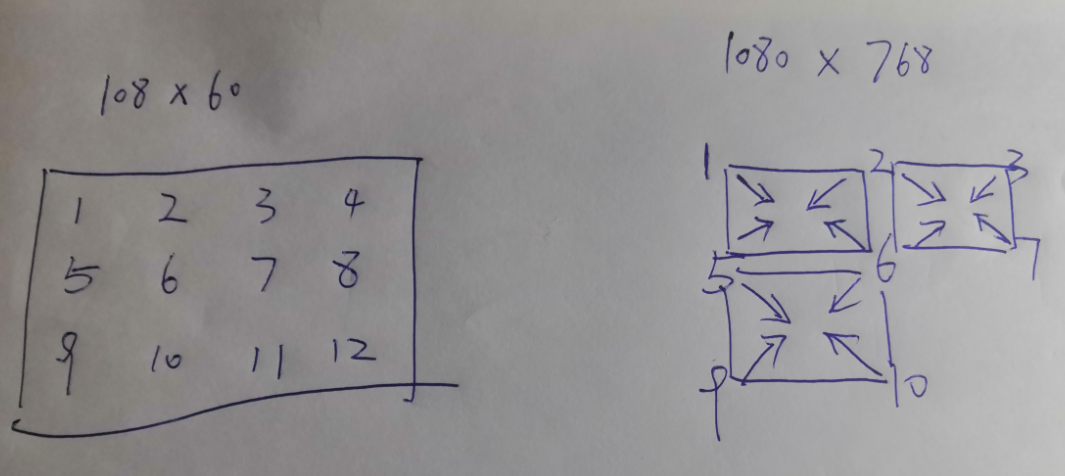
我们想得到一张放大的图片，现在有原图像和目标图像。那么，有一个最基本的问题摆在我们面前：是遍历原图像呢，还是遍历目标图像呢？

在实践的过程中，通常都是遍历目标图像的。因为这样可以确保目标图像的每一个像素都是有值的。

就拿上图的例子来说，右图目标图像中的 [0,0] 点很顺利的找到了左图原图像中与自己对应的 [0,0] 点。然后 [0,1] 点就懵逼了，它应该找[0,0.33]点吗？没有这个点啊，所以[0,0.33]的值是需要四个点来进行拟态的。

插值法除了双线性插值还有最临近插值，线性插值。

最临近插值可以理解为取值为最近的一个像素点，线性插值是在周围两个像素点中取一个(根据两边距离决定)折中值，很明显它们的作用范围均是线性一维。

再来说双线性插值，它可以取空间中的四个点来做拟态取值。

大概理解就是如此，具体实现可以借助公式,下面给出百度百科的公式。

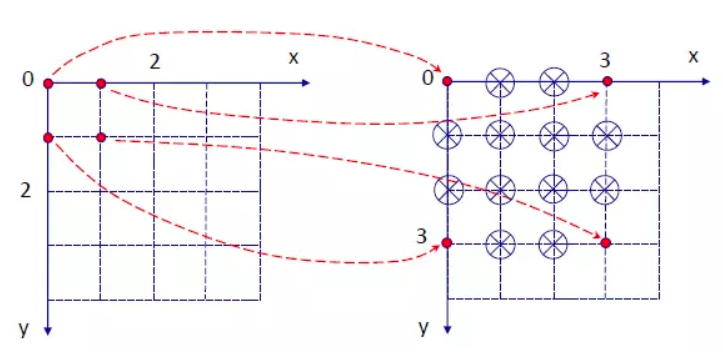
已知的红色数据点与待插值得到的绿色点

假如我们想得到未知函数f在点P= (x,y) 的值，假设我们已知函数f在Q11 = (x1,y1)、Q12 = (x1,y2),Q21 = (x2,y1) 以及Q22 = (x2,y2) 四个点的值。

首先在x方向进行线性插值，得到R1和R2，然后在y方向进行线性插值，得到P.
这样就得到所要的结果f(x,y).

其中红色点Q11,Q12,Q21,Q22为已知的4个像素点.

第一步：X方向的线性插值，在Q12,Q22中插入蓝色点R2，Q11，Q21中插入蓝色点R1；

第二步 ：Y方向的线性插值 ,通过第一步计算出的R1与R2在y方向上插值计算出P点。

线性插值的结果与插值的顺序无关。首先进行y方向的插值，然后进行x方向的插值，所得到的结果是一样的。双线性插值的结果与先进行哪个方向的插值无关。

如果选择一个坐标系统使得 的四个已知点坐标分别为 (0, 0)、(0, 1)、(1, 0) 和 (1, 1)，那么插值公式就可以化简为

f(x,y)=f(0,0)(1-x)(1-y)+f(1,0)x(1-y)+f(0,1)(1-x)y+f(1,1)xy

在x与y方向上，z值成单调性特性的应用中，此种方法可以做外插运算，即可以求解Q1~Q4所构成的正方形以外的点的值。

f(x,y1) ≈ (x2−x / x2−x1) * f(Q11) + (x−x1 / x2−x1) * f(Q21),
f(x,y2) ≈ (x2−x / x2−x1) * f(Q12) + (x−x1 / x2−x1) * f(Q22).
f(x,y) ≈ (y2−y / y2−y1) * f(x,y1) + (y−y1 / y2−y1) * f(x,y2)

int index = 0 ;
for(y=0;y<768;y++){
for(x=0;x<1080;x++){
for(int i=0;i<60;i++){
for(int j=0;j<108;j++){
int getx1 = ((108+13-y)/13)*bmp[index*108+60] + (y/13)*bmp[index*108+60+1] ;
int getx2 = ((108+13-y)/13)*bmp[(index+1)*108+60] + (y/13)*bmp[(index+1)*108+60+1] ;
int getRgb = (i/10)*getx1 + ((60-i)/10)*getx2 ;
print_image(x,y,getRgb);
}
}
}
index ++ ;
}