方向导数、梯度、法线间的关系

在读书时候，数学里的好多东西记不清楚了感觉很模糊，所以为了加深印象防止遗忘所以记录一下，博客中参考的资料已在文末标明。博客中要是有啥错误，或者不好的地方欢迎指出一起探讨，嘿嘿。

 

方向导数：

函数在点P处，沿着方向V的变化率大小，得到结果是一个数值。

对于一个二元函数,其方向导数为（word里面写好公式复制不上来，气人只能截图）

 

证明如下：由

 

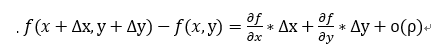
两边同时除以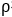得到下式子：

 

梯度：

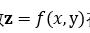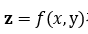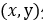　　梯度这个东东是一个向量，既有大小也有方向。设函数在平面区域D内具有一阶连续偏导数，那么对于每一个点，都可以求出一个向量：这个向量就是在点处的梯度。

 

为什么梯度的方向是函数变化最快的方向？

       对于点由上面可知其方向导数为，由此可以推出下式子：

 

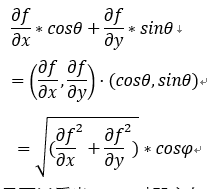
　　为两个梯度与所选方向间的夹角，明显可以看出时即方向一致时所得到的方向导数最大即函数变化率最大。

 

梯度与法线的关系：

　　对于一个曲面，法线为与切平面垂直的直线。那么对一般的二元函数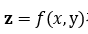,这个曲面被平面z=c所截下来的曲线L在平面xOy上面的投影为等高线。由于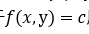所以两边同时对x求微分可得下式子：

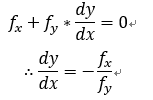
　　然后我们通过求切线的方式来求得法线：

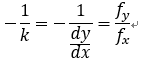
　　这正好也是梯度方向，所以说等高线上点P的法向量与该点的梯度方向相同。

      

 

参考：https://blog.csdn.net/myarrow/article/details/51332421

http://netedu.xauat.edu.cn/jpkc/netedu/jpkc/gdsx/homepage/5jxsd/51/513/5308/530807.htm