实验4 函数和数组

任务一

该实验可以以返回值的形式返回根。

只需要将函数类型更替为double等有返回值类型，并返回即可。

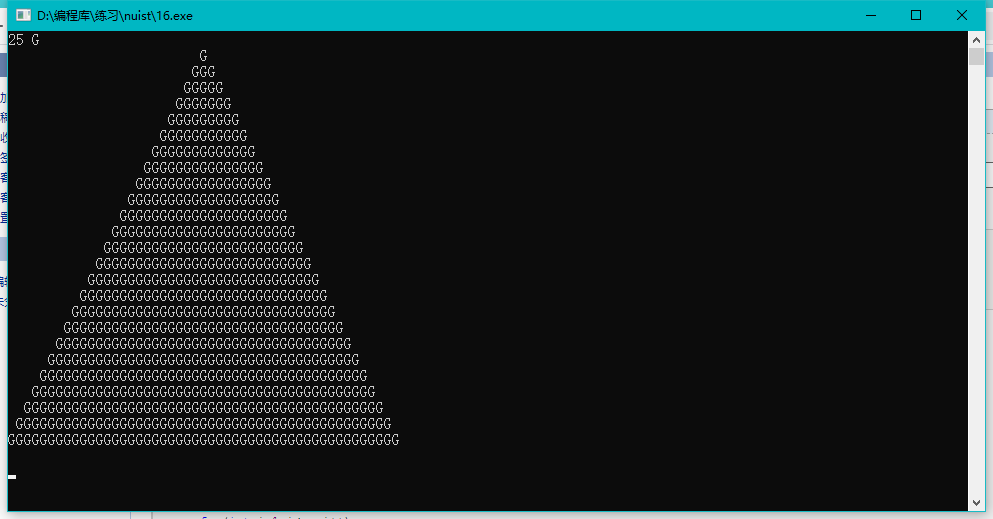
任务二

 

#include <stdio.h>
long long fac(int n);
int main() 
{
    int i,n;
    printf("Enter n:");
    scanf("%d",&n);
    for(i=1;i<=n;++i)
    printf("%d!=%lld\n",i,fac(i));
    return 0;
}
long long fac(int n) 
{
    static long long p=1;
    printf("p = %lld\n", p);
    p=p*n;
    return p;
}

 

 

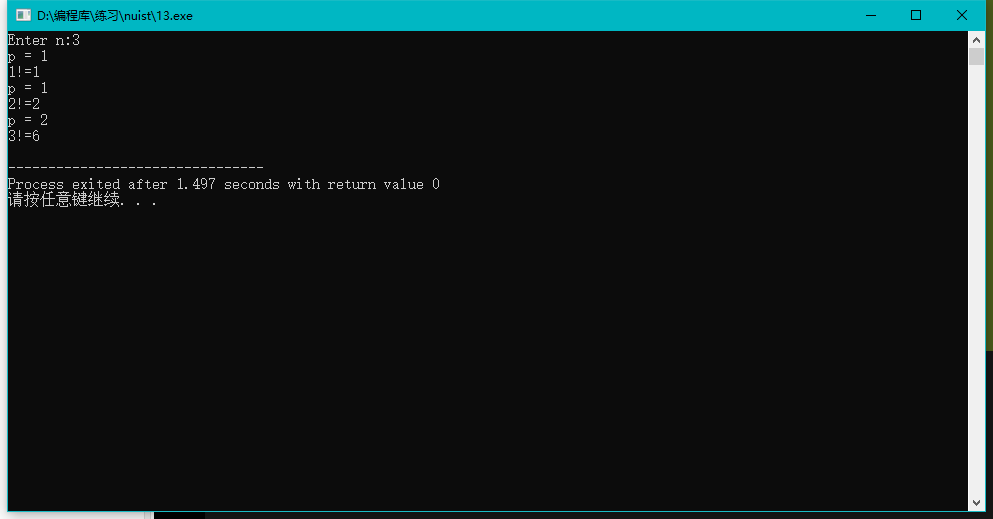
任务三

#include<stdio.h>
#define N 1000
int fun(int n,int m,int bb[N]) 
{
    int i,j,k=0,flag;
    for(j=n;j<=m;j++) 
    {
        flag=1;
        for(i=2;i<j;i++)
        if(j%i==0) 
        {
            flag=0;
            break;
        }
        if(flag)
        bb[k++]=j;
    }
    return k;
}
int main()
{
    int n=0,m=0,i,k,bb[N];
    scanf("%d",&n);
    scanf("%d",&m);
    for(i=0;i<m-n;i++)
    bb[i]=0;
    k=fun(n,m,bb);
    for(i=0;i<k;i++)
    printf("%4d",bb[i]);
    return 0;
}

 

 

 

 

 

任务四

#include <stdio.h>
long long fun(int n);//声明函数 
int main() 
{
    int n;//设定一个输入 
    long long f;//设定一个输出 
    while(scanf("%d",&n)!=EOF)//多组输入 
    {
        f=fun(n);//调用函数 
        printf("n=%d,f=%lld\n",n,f);//打印结果 
    }
    return 0;
}
long long fun(int n)//定义函数 
{
    static long long a=1;//初始化2的0次方 
    static int i=0;//判断是否递归回到第一次 
    static long long b;
    if(n)//判断是否继续递归并累计乘2次数，嘤嘤嘤 
    {
    n--;
    i++;
    fun(n);//强行递归大法，嘤嘤嘤 
    }
    if(i)//判断是否乘2 
    {
    i--;
    a=a*2;
    }
    else//如果不是就减1并返回一个值 
    {
    b=a-1;//存储返回值 
    a=1;//初始化 
    return b;
    }
}

 

 

 

#include <stdio.h> 
int main() 
{
    int n;//设定一个输入 
    long long f;//设定一个输出 
    while(scanf("%d",&n)!=EOF)//多组输入 
    {
        int b[1000]={1};//多达一千位的输出，嘤嘤嘤
        int temp=0;
        for(int i=0;i<n;i++)//迭代算法，递归太麻烦了Orz 
        {
            if(b[0]<=1000)//减少执行次数。。。。
             b[0]*=2;
           else
           {
                   int c=b[0];
                   for(int i=0;i<1000;i++)//高精度，你懂的。
                   {    
                   b[i]=b[i]*c+temp; 
                       temp=b[i]/10;
                       b[i]%=10;
                   }
           }
        } 
        if(b[0]>0)//减1操作。。。。枯了 
        b[0]-=1;
        else
        {
            for(int j=1;j<1000;j++)
            {
                if(b[j]!=0)
                {
                    b[j]-=1;
                    break;
                }
            }
        }
        int x=1000-1;
        for(;x>=0;x--)//输出判断 
        if(b[x]!=0)
        break;
        for(;x>=0;x--)//打印输出 
        printf("%d",b[x]);
        printf("\n"); 
    } 
    return 0;
}

 

 加个高精度，再加一个减1的判断。不难，但是码代码让我吐了，特别是前面的递归。

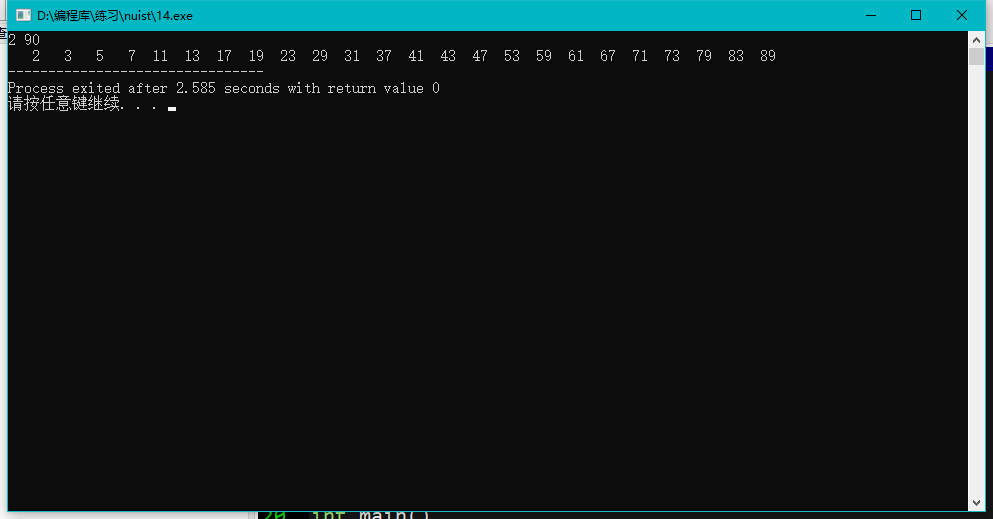
任务五

 

#include <stdio.h>
void draw(int n, char symbol);
int main() 
{
    int n, symbol;
    while(scanf("%d %c", &n, &symbol) != EOF) 
    {
        draw(n, symbol); 
        printf("\n");
    }
    return 0;
}
void draw(int n,char symbol)
{
    for(int i=1;i<=n;i++)
    {
        for(int j=n-i;j>0;j--)
        printf(" ");
        for(int j=1;j<=(2*i-1);j++)
        printf("%c",symbol);
        printf("\n");
    }
    return;
}