BZOJ 1965 [Ahoi2005]SHUFFLE 洗牌：快速幂 + 逆元

题目链接：http://www.lydsy.com/JudgeOnline/problem.php?id=1965

题意：

　　对于扑克牌的一次洗牌是这样定义的，将一叠N（N为偶数）张扑克牌平均分成上下两叠，取下面一叠的第一张作为新的一叠的第一张，然后取上面一叠的第一张作为新的一叠的第二张，再取下面一叠的第二张作为新的一叠的第三张……如此交替直到所有的牌取完。

　　如果对一叠6张的扑克牌1 2 3 4 5 6，进行一次洗牌的过程如下图所示：

　　

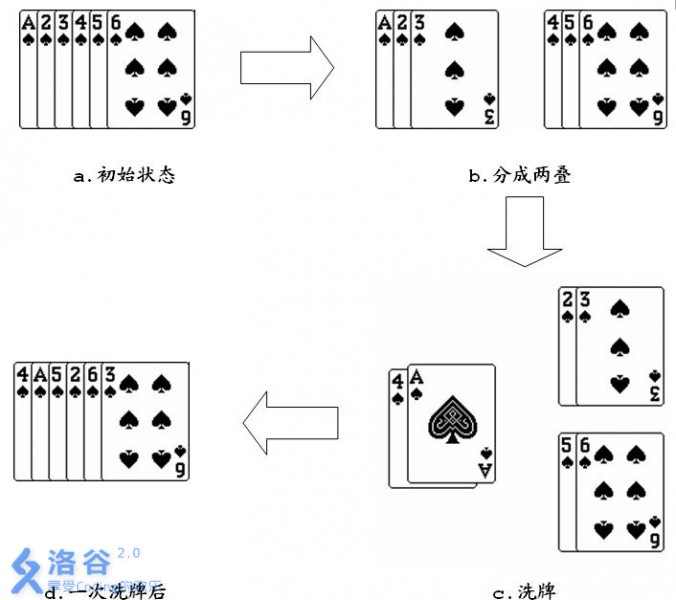
　　游戏是这样的，如果给定长度为N的一叠扑克牌，并且牌面大小从1开始连续增加到N（不考虑花色），对这样的一叠扑克牌，进行M次洗牌。最先说出经过洗牌后的扑克牌序列中第L张扑克牌的牌面大小是多少的科学家得胜。小联想赢取游戏的胜利，你能帮助他吗？

 

题解：

　　对于一张牌，若当前位置为x，则一次洗牌后，位置变为(x*2)%(n+1)。

　　所以m次洗牌后，位置为L = (x * 2^m) % (n+1)。

　　所以原来的位置x = L * (2^m关于n+1的逆元) % (n+1)

 

AC Code:

#include <iostream>
#include <stdio.h>
#include <string.h>

using namespace std;

long long n,m,l;

void exgcd(long long a,long long b,long long &x,long long &y)
{
    if(b==0)
    {
        x=1,y=0;
        return;
    }
    exgcd(b,a%b,y,x);
    y-=(a/b)*x;
}

long long inv(int i,int p)
{
    long long x,y;
    exgcd(i,p,x,y);
    return (x%p+p)%p;
}

long long quick_pow(long long x,long long k,long long p)
{
    long long ans=1;
    while(k>0)
    {
        if(k&1) ans=ans*x%p;
        x=x*x%p,k>>=1;
    }
    return ans;
}

int main()
{
    cin>>n>>m>>l;
    cout<<(l*inv(quick_pow(2,m,n+1),n+1))%(n+1)<<endl;
}