BZOJ 1201 [HNOI2005]数三角形：枚举 + 前缀和

题目链接：http://www.lydsy.com/JudgeOnline/problem.php?id=1201

题意：

　　有一个边长为n的正三角形网格，去掉其中一些线段，问你在这幅图中有多少个三角形。

 

题解：

　　枚举 + 前缀和。

 

　　三角形总共有两种：正着放的、倒着放的。

　　分别处理就好。

　　总复杂度 < O(N^3)

 

　　为了判断某一个三角形是否存在，需要迅速判断它的三边是否都是实线（不断开）。

　　所以建立三个前缀和，分别代表左、右、底边在对应方向上的边长和。

　　若某一边上的区间和[a,b] == b-a+1，则为实线。

　　如图为前缀和方向：

　　

 

 

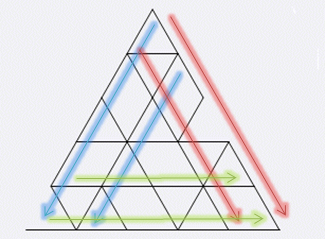
　　正着放的：

　　　　N^2枚举三角形最顶上的小三角形，再套一个for枚举向下延伸的边长k。

　　

 

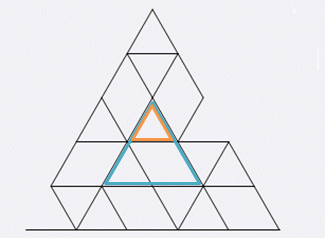
　　倒着放的：

　　　　倒三角形底部有一个小倒三角形，枚举它左边相邻的小正三角。

　　

 

AC Code:

 1 #include <iostream>
 2 #include <stdio.h>
 3 #include <string.h>
 4 #define MAX_N 1005
 5 
 6 using namespace std;
 7 
 8 int n;
 9 int ans=0;
10 int l[MAX_N][MAX_N];
11 int r[MAX_N][MAX_N];
12 int b[MAX_N][MAX_N];
13 int lef[MAX_N][MAX_N];
14 int rig[MAX_N][MAX_N];
15 int btm[MAX_N][MAX_N];
16 
17 void read()
18 {
19     memset(l,0,sizeof(l));
20     memset(r,0,sizeof(r));
21     memset(b,0,sizeof(b));
22     cin>>n;
23     for(int i=1;i<=n;i++)
24     {
25         for(int j=1;j<=i;j++)
26         {
27             cin>>l[i][j]>>r[i][j]>>b[i][j];
28         }
29     }
30 }
31 
32 void cal_sum()
33 {
34     memset(lef,0,sizeof(lef));
35     memset(rig,0,sizeof(rig));
36     memset(btm,0,sizeof(btm));
37     for(int i=1;i<=n;i++)
38     {
39         for(int j=1;j<=i;j++)
40         {
41             lef[i][j]=lef[i-1][j]+l[i][j];
42             rig[i][j]=rig[i-1][j-1]+r[i][j];
43             btm[i][j]=btm[i][j-1]+b[i][j];
44         }
45     }
46 }
47 
48 void find_tri()
49 {
50     for(int i=1;i<=n;i++)
51     {
52         for(int j=1;j<=i;j++)
53         {
54             for(int k=1;;k++)
55             {
56                 if(lef[i+k-1][j]-lef[i-1][j]<k) break;
57                 if(rig[i+k-1][j+k-1]-rig[i-1][j-1]<k) break;
58                 if(btm[i+k-1][j+k-1]-btm[i+k-1][j-1]<k) continue;
59                 ans++;
60             }
61         }
62     }
63     for(int i=1;i<=n;i++)
64     {
65         for(int j=1;j<i;j++)
66         {
67             for(int k=1;i-k>=0 && j-k>=0;k++)
68             {
69                 if(lef[i][j+1]-lef[i-k][j+1]<k) break;
70                 if(rig[i][j]-rig[i-k][j-k]<k) break;
71                 if(btm[i-k][j]-btm[i-k][j-k]<k) continue;
72                 ans++;
73             }
74         }
75     }
76 }
77 
78 void solve()
79 {
80     cal_sum();
81     find_tri();
82 }
83 
84 void print()
85 {
86     cout<<ans<<endl;
87 }
88 
89 int main()
90 {
91     read();
92     solve();
93     print();
94 }

 

posted @ 2017-09-14 01:47  Leohh  阅读(246)  评论(0)  编辑  收藏  举报