RQNOJ 328 炮兵阵地:状压dp
题目链接:https://www.rqnoj.cn/problem/328
题意:
司令部的将军们打算在N*M的网格地图上部署他们的炮兵部队。
一个N*M的地图由N行M列组成(N≤100,M≤10),地图的每一格可能是山地(用'H' 表示),也可能是平原(用'P'表示),如下图。
在每一格平原地形上最多可以布置一支炮兵部队(山地上不能够部署炮兵部队);
一支炮兵部队在地图上的攻击范围如图中黑色区域所示:
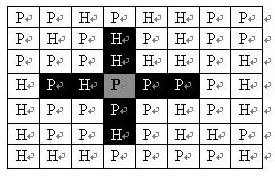
如果在地图中的灰色所标识的平原上部署一支炮兵部队,则图中的黑色的网格表示它能够攻击到的区域:沿横向左右各两格,沿纵向上下各两格。
图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。
现在,将军们规划如何部署炮兵部队,在防止误伤的前提下(保证任何两支炮兵部队之间不能互相攻击,即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内)。
问在整个地图区域内最多能够摆放多少我军的炮兵部队。
题解:
表示状态:
m<=10,所以对每一行进行压缩。
dp[i][state1][state2] = max num of cannons(炮兵数量)
i:该摆第i行
state1:上上一行的状态(i-2)
state2:上一行的状态(i-1)
找出答案:
max dp[n][state1][state2]
枚举state1,state2.
如何转移:
now: dp[i][state1][state2]
枚举第i行填的方案为nex。
如果nex符合第i行的地形,并且与state1,state2均没有交集,则:
dp[i+1][state2][nex] = max dp[i][state1][state2] + sum[nex]
(sum[nex]为方案nex中的炮兵个数。)
边界条件:
dp[0][0][0] = 0
others = -1
(第0行的上两行方案均设为0,因为不填适用于任何地形)
优化:
(1)预处理field数组。
field[i]为第i行的地形。每一位上1位山地,0为平原。
判断nex是否适用于第i行时,只需判断是否有 state & field == 0
(2)预处理在一行上的合法方案。
在每一行上,两个炮兵之间最少相距2格。利用此性质dfs然后存起来就好。
(3)dp数组的下标state不再直接表示01状态,而是换成s代表当前方案在dfs数组中的索引。
省空间啊。。。
(4)预处理出每一种行上合法方案的sum值,存起来。
预处理时,最好用lowbit直接找出1,而不用逐位枚举。
AC Code:
1 // optimizations: 2 // scheme: put == 1, blank == 0 3 // field: mountain == 1, plain == 0 4 // legal: scheme & field == 0 5 // preprocess: legal scheme for rows 6 // 7 // state expression: 8 // dp[i][state1][state2] = max num of cannons 9 // i: considering ith row 10 // state1: top row 11 // state2: bottom row 12 // 13 // find the answer: 14 // max dp[n][state1][state2] 15 // 16 // transferring: 17 // now: dp[i][state1][state2] 18 // if nex & field[i] == 0 19 // dp[i+1][state2][nex] = max dp[i][state1][state2] + sum[nex] 20 // 21 // boundary: 22 // dp[0][0][0] = 0 23 // others = -1 24 #include <iostream> 25 #include <stdio.h> 26 #include <string.h> 27 #include <stack> 28 #define MAX_N 105 29 #define MAX_M 15 30 #define MAX_S 65 31 32 using namespace std; 33 34 int n,m; 35 int cnt; 36 int ans; 37 int sum[MAX_S]; 38 int field[MAX_N]; 39 int legal_state[MAX_S]; 40 int dp[MAX_N][MAX_S][MAX_S]; 41 42 void dfs(int col,int state) 43 { 44 if(col>=m) 45 { 46 legal_state[cnt++]=state; 47 return; 48 } 49 dfs(col+1,state); 50 dfs(col+3,state|(1<<col)); 51 } 52 53 int cal_sum(int state) 54 { 55 int lowbit=state&-state; 56 int cnt=0; 57 while(lowbit) 58 { 59 cnt++; 60 state^=lowbit; 61 lowbit=state&-state; 62 } 63 return cnt; 64 } 65 66 void read() 67 { 68 memset(field,0,sizeof(field)); 69 cin>>n>>m; 70 char c; 71 for(int i=0;i<n;i++) 72 { 73 for(int j=0;j<m;j++) 74 { 75 cin>>c; 76 field[i]<<=1; 77 if(c=='H') field[i]|=1; 78 } 79 } 80 } 81 82 void solve() 83 { 84 cnt=0; 85 dfs(0,0); 86 for(int i=0;i<cnt;i++) 87 { 88 sum[i]=cal_sum(legal_state[i]); 89 } 90 memset(dp,-1,sizeof(dp)); 91 dp[0][0][0]=0; 92 for(int i=0;i<n;i++) 93 { 94 for(int s1=0;s1<cnt;s1++) 95 { 96 for(int s2=0;s2<cnt;s2++) 97 { 98 int state1=legal_state[s1]; 99 int state2=legal_state[s2]; 100 if(dp[i][s1][s2]!=-1 && !(state1&state2)) 101 { 102 for(int s3=0;s3<cnt;s3++) 103 { 104 int nex=legal_state[s3]; 105 if(!(nex&field[i]) && !(nex&state1) && !(nex&state2)) 106 { 107 dp[i+1][s2][s3]=max(dp[i+1][s2][s3],dp[i][s1][s2]+sum[s3]); 108 } 109 } 110 } 111 } 112 } 113 } 114 ans=0; 115 for(int s1=0;s1<cnt;s1++) 116 { 117 for(int s2=0;s2<cnt;s2++) 118 { 119 ans=max(ans,dp[n][s1][s2]); 120 } 121 } 122 } 123 124 void print() 125 { 126 cout<<ans<<endl; 127 } 128 129 int main() 130 { 131 read(); 132 solve(); 133 print(); 134 }

