AOP编程在目前来说好像是大家都比较喜欢的。ASP.NET MVC中的Filter就是使用AOP实现的配置器模式。AOP在编码中的应用主要有如下几个方面:
日志记录,跟踪,优化和监控
事务的处理
持久化
性能的优化
资源池,如数据库连接池的管理
系统统一的认证、权限管理等
应用系统的异常捕捉及处理
针对具体行业应用的横切行为
前面几种应用我相信大家都是比较熟悉的。在ASP.NET MVC中有Filter之类的,提供认证和权限管理。很多实现AOP的组件都是拿日志作为例子说明。我这里给大家说明一个具体业务的横切例子。
以之前的Orchard.Car模块为例,如果我们这个模块式产品中的一个模块,当应用到项目中时,可能需要一些改动,那么AOP就可以在很多时候解决我们的问题。
假设我们现在有一个方法是获取Car的列表,那么对应的代码如下:
对应的Service代码如下:
别忘了在Route.cs中添加路由代码。
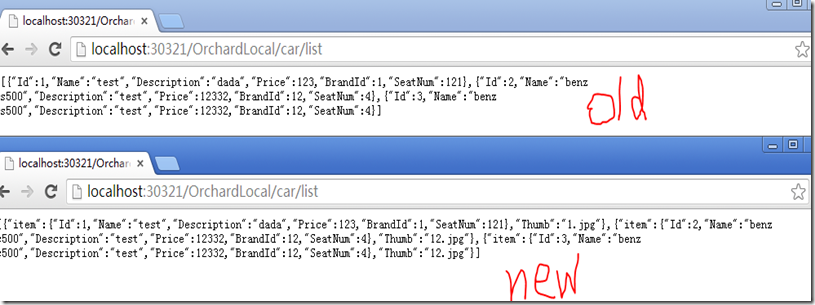
运行,查看结果:
如果在产品发布后,项目A中使用该产品,需要为car添加一个字段,叫做缩略图,那么很现实的一个问题是,我们是不是为了项目A单独为car扩展一个字段?这时候适配器就很重要了,实现适配器的方式有很多,我们这里就说明下如何使用AOP来实现字段的扩展。
首先需要一个Aufofac的module类,代码如下:
我们只需要为CarInfoService类来添加一个拦截器,别的就没有必要了。这里你会看到有一个SimpleInterceptor类,它的作用就是用来对CarInfoService的方法进行拦截。
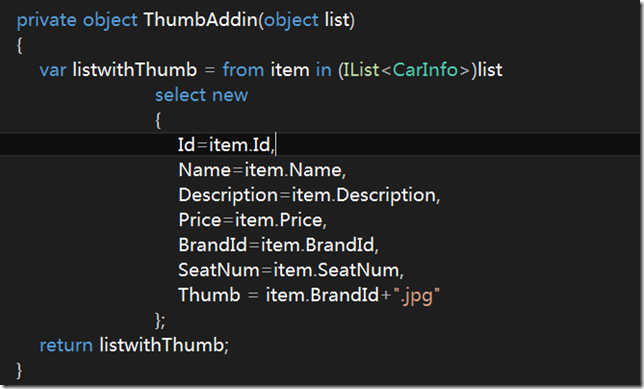
SimpleInterceptor的代码如下:
如果当前的方法名称是GetList那么我们就为它添加一个字段,代表缩略图。这里我随便写一个,你可以根据自己的实际需要去做相应的改变。
现实中,可能这个Interceptor是在一个扩展模块中,所以对应的需要一个扩展的服务来提供Thumb字段。
结果不正确,因为我们客户端或者页面已经对运来的JSON进行了解析,所以新的JSON格式不是我们需要的,再次修改Interceptor的代码:
除了GetList方法可以通过AOP实现修改封闭扩展开放,你叶可以使用这种方式来扩展新增记录的方法。这时你需要把Request.Form从Controller中传入Service方法。这种扩展方式一个很大的好处就是可以帮助多个项目平稳的升级。产品模块的代码永远都不会被项目牵制。
具体的例子请到github上下载相应的代码来查看,这里就不做解释了。
上面只是我自己的一个小小的使用经验,有时候当字段的类型需要更改,而你不允许直接更改当前的代码时,这种方式也是一个不错的方法。
AOP虽然不是标准的设计模式之一,但是通过它可以让很多的模式更加简单的实现。
最后说明一下,OrchardNoCMS中如何实现的AOP。
它使用的Castle.DynamicProxy来实现的。结合Autofac。首先是对AutoFac的扩展类:
注入时,需要为注入的Component调用EnableDynamicProxy方法,代码位置:
可以看出来,所有实现继承了IDependency的类都可以使用AOP。
以上就是OrchardNoCMS的AOP编程示例,可以到https://github.com/nicholaspei/OrchardNoCMS 下载完整代码。
二叉查找树
二叉查找树(Binery Search Tree),要么是一颗空树,要么是具有以下性质的二叉树:
(1) 要是结点的左子树不为空,则左子树的所有结点的值小于该结点的值
(2) 要是结点的右子树不为空,则右子树的所有结点的值大于该结点的值
(3) 该结点的左右子树也是二叉查找树
二叉查找树通常用二叉链表存储结点。中序遍历二叉查找树可以得到关键字有序的序列,一个无序的序列可以通过构造一棵二叉查找树,再中序遍历得到一棵有序的链表。每次插入的位置都是叶子结点,插入时不用移动其他结点。搜索、插入、删除结点的复杂度为树高,即O(logn)(数列有序,退化成线性表,此时的复杂度为O(n))。
查找
二叉查找树T查找关键字val的过程为:
- 若T为空树,查找失败,否则:
- 若val 等于T的关键字,查找成功,返回。否则
- 若val 小于T的关键字,继续查找T的左子树。否则
- 查找T的右子树。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
bool SearchBST(BiTree T, int val, BiTree f, BiTree &p){ if(!T) { p = f; return false; } else if(val == T->data) { p = T; return true; } else if(val < T->data) SearchBST(T->left, val, T, p); else SearchBST(T->right, val, T, p);} |
插入
二叉查找树T插入关键字为val的结点s过程为:
如果在二叉查找树T中没有找到关键字为val的结点(查找过程返回的结点为p):
- 如果p为空,则s直接赋给p
- 如果val小于p的关键字,插入到p的左子树上
- 如果val大于p的关键字,插入到p的右子树上
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
bool InsertBST(BiTree &T, int val){ BiTree p = NULL; if(!SearchBST(T, val, NULL, p)) { BiTree node = new BiTNode; node->data = val; node->left = node->right = NULL; if(!p) T = node; else if(val < p->data) p->left = node; else p->right = node; return true; } return false;} |
删除
删除结点为p
- 若p为叶子结点,直接删掉
- 若p只有左子树,则把自己替换成左子树
- 若p只有右子树,则把自己替换成右子树
- 若左右子树都有,则把自己的关键字替换成左子树中最靠右的关键字,同时干掉最右边的关键字
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
|
bool Delete(BiTree &T){ if(!T->left && !T->right) { delete T; T = NULL; } else if(!T->left) { BiTree p = T; T = T->right; delete p; p = NULL; } else if(!T->right) { BiTree p = T; T = T->left; delete p; p = NULL; } else { BiTree p = T, q = T->left; while(q->right) { p = q; q = q->right; } if(T == p) { T->data = q->data; T->left = q->left; delete q; q = NULL; } else { T->data = q->data; p->right = NULL; delete q; q = NULL; } } return true;}bool DeleteBST(BiTree &T, int val){ if(!T) return false; else { if(val == T->data) return Delete(T); else if(val < T->data) return DeleteBST(T->left, val); else return DeleteBST(T->right, val); }} |
完整参考代码
#include <iostream>
#include <vector>
using namespace std;
typedef struct BiTNode
{
int data;
BiTNode *left;
BiTNode *right;
}BiTNode, *BiTree;
bool SearchBST(BiTree T, int val, BiTree f, BiTree &p)
{
if(!T)
{
p = f;
return false;
}
else if(val == T->data)
{
p = T;
return true;
}
else if(val < T->data)
SearchBST(T->left, val, T, p);
else
SearchBST(T->right, val, T, p);
}
bool InsertBST(BiTree &T, int val)
{
BiTree p = NULL;
if(!SearchBST(T, val, NULL, p))
{
BiTree node = new BiTNode;
node->data = val;
node->left = node->right = NULL;
if(!p)
T = node;
else if(val < p->data)
p->left = node;
else
p->right = node;
return true;
}
return false;
}
bool Delete(BiTree &T)
{
if(!T->left && !T->right)
{
delete T;
T = NULL;
}
else if(!T->left)
{
BiTree p = T;
T = T->right;
delete p;
p = NULL;
}
else if(!T->right)
{
BiTree p = T;
T = T->left;
delete p;
p = NULL;
}
else
{
BiTree p = T, q = T->left;
while(q->right)
{
p = q;
q = q->right;
}
if(T == p)
{
T->data = q->data;
T->left = q->left;
delete q;
q = NULL;
}
else
{
T->data = q->data;
p->right = NULL;
delete q;
q = NULL;
}
}
return true;
}
bool DeleteBST(BiTree &T, int val)
{
if(!T)
return false;
else
{
if(val == T->data)
return Delete(T);
else if(val < T->data)
return DeleteBST(T->left, val);
else
return DeleteBST(T->right, val);
}
}
void InorderTraversal(BiTree T)
{
if(T)
{
InorderTraversal(T->left);
cout << T->data << endl;
InorderTraversal(T->right);
}
}
int main()
{
int array[] = {7, 2, 10, 9, 2, 0, 1};
int len_array = sizeof(array) / sizeof(*array);
vector<int> vec(array, array + len_array);
BiTree root = NULL;
for(vector<int>::iterator beg = vec.begin(), end = vec.end();
beg != end; ++ beg)
{
InsertBST(root, *beg);
}
InorderTraversal(root);
DeleteBST(root, 10);
cout << endl;
InorderTraversal(root);
cout << endl;
DeleteBST(root, 1);
InorderTraversal(root);
}