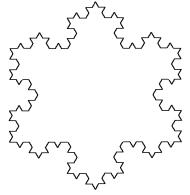
图1-1 雪花图形
前两天在一个网页上看到了雪花,感觉很漂亮,就搜索了下,发现了这个Koch曲线(大概很多人都早就知道(︸_︸)),看上去很漂亮,简单的分形,简洁的递归,就是美丽的图案。
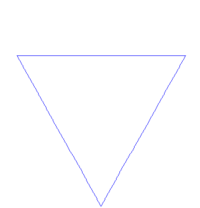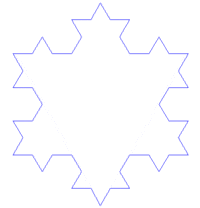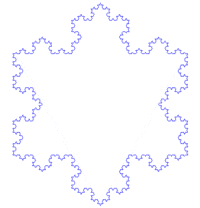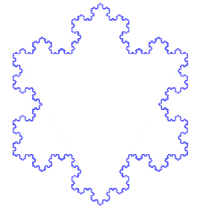
图1-2 维基百科分形条目中的koch(科赫)曲线图例,非常明了。
HTML5中加入了canvas标签,可以方便的绘制简单或复杂的图形。canvas的使用比较简单,这次只用到它的画线功能。
简单介绍下canvas的使用:
var canvas = document.getElementById("cantest"); //获取canvas对象
if(canvas.getContext){ //可以通过这种方式检测浏览器是否支持canvas标签
canvas.height = canvas.height; //重设canvas的宽或高可以清空标签中的图案,相当于clear()
var ctx = canvas.getContext("2d"); //获取画布上的绘图环境
ctx.strokeStyle = "#fff"; //设置画笔的颜色,支持css样式的颜色表现方式,可以用rgb(r, g, b)和rgba(r, g, b, a)这样的方式
ctx.beginPath(); //丢弃任何当前定义的路径并且开始一条新的路径。它把当前的点设置为 (0,0)。
ctx.moveTo(5, 5); //移动“画笔”到点(5, 5),就像把笔拿起来,然后放到(5, 5)的位置上
ctx.lineTo(10, 10); //画线到点(10, 10),从现在的画笔落点,画直线一直到点(10, 10)
ctx.stroke(); //开始绘制,把刚才所划定的区域“勾勒”轮廓。fill方法用来填充。
}else{
alert("不支持Canvas");
}
if(canvas.getContext){ //可以通过这种方式检测浏览器是否支持canvas标签
canvas.height = canvas.height; //重设canvas的宽或高可以清空标签中的图案,相当于clear()
var ctx = canvas.getContext("2d"); //获取画布上的绘图环境
ctx.strokeStyle = "#fff"; //设置画笔的颜色,支持css样式的颜色表现方式,可以用rgb(r, g, b)和rgba(r, g, b, a)这样的方式
ctx.beginPath(); //丢弃任何当前定义的路径并且开始一条新的路径。它把当前的点设置为 (0,0)。
ctx.moveTo(5, 5); //移动“画笔”到点(5, 5),就像把笔拿起来,然后放到(5, 5)的位置上
ctx.lineTo(10, 10); //画线到点(10, 10),从现在的画笔落点,画直线一直到点(10, 10)
ctx.stroke(); //开始绘制,把刚才所划定的区域“勾勒”轮廓。fill方法用来填充。
}else{
alert("不支持Canvas");
}
绘制Koch曲线用到函数只有这么多,重点是数学公式。
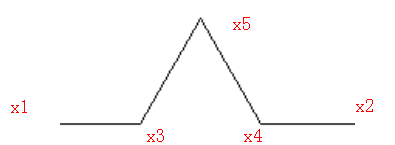
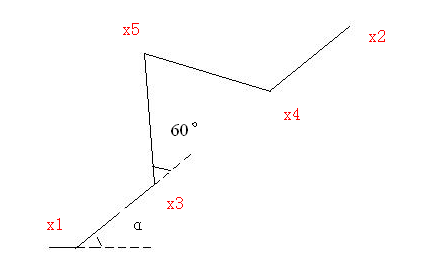
图1-3 规定最简单的曲线中的一条的所用五个点的表示
再高维度的Koch曲线最终都可以分解为如图1-3所示的这样一条线,其中的4条线段都相当,中间的三角形为全等三角形。
在绘制时,我们只要知道x1和x2的值,就可以相应的计算出x3、x4和x5的值。
先计算水平位置的各个点的公式,然后再扩展到各个角度,得到统一的公式,过程就不写了,也参考了一些资料(Koch曲线的构造及性质)。最终的公式如下:
var x3 = (x2 - x1) / 3 + x1;
var y3 = (y2 - y1) /3 + y1;
var x4 = (x2 - x1) / 3 * 2 + x1;
var y4 = (y2 - y1) / 3 * 2 + y1;
var x5 = x3 + ((x2 - x1) - (y2 - y1) * Math.sqrt(3)) / 6;
var y5 = y3 + ((x2 - x1) * Math.sqrt(3) + (y2 - y1)) / 6;
var y3 = (y2 - y1) /3 + y1;
var x4 = (x2 - x1) / 3 * 2 + x1;
var y4 = (y2 - y1) / 3 * 2 + y1;
var x5 = x3 + ((x2 - x1) - (y2 - y1) * Math.sqrt(3)) / 6;
var y5 = y3 + ((x2 - x1) * Math.sqrt(3) + (y2 - y1)) / 6;
现在就可以整理代码了,实现的基本思路当然是递归。 首先在页面中加入canvas标签。 <canvas id="cantest" width="500px" height="500px"></canvas>
canvas可以通过css样式设置,这里只加上了边框和背景色。
主体方法就是递归函数:
function koch(ctx, x1, y1, x2, y2, n, m){ //ctx为绘图对象,x1,y1,x2,y2为两头的点,n为当前维度,m为维度
if(m == 0){
ctx.moveTo(x1, y1);
ctx.lineTo(x2, y2);
ctx.stroke();
return false;
}
var x3 = (x2 - x1) / 3 + x1;
var y3 = (y2 - y1) /3 + y1;
var x4 = (x2 - x1) / 3 * 2 + x1;
var y4 = (y2 - y1) / 3 * 2 + y1;
var x5 = x3 + ((x2 - x1) - (y2 - y1) * Math.sqrt(3)) / 6;
var y5 = y3 + ((x2 - x1) * Math.sqrt(3) + (y2 - y1)) / 6;
n = n + 1;
if(n == m){
ctx.moveTo(x1, y1);
ctx.lineTo(x3, y3);
ctx.lineTo(x5, y5);
ctx.lineTo(x4, y4);
ctx.lineTo(x2, y2);
ctx.stroke();
return false;
}
koch(ctx, x1, y1, x3, y3, n, m)
koch(ctx, x3, y3, x5, y5, n, m)
koch(ctx, x5, y5, x4, y4, n, m)
koch(ctx, x4, y4, x2, y2, n, m)
}
if(m == 0){
ctx.moveTo(x1, y1);
ctx.lineTo(x2, y2);
ctx.stroke();
return false;
}
var x3 = (x2 - x1) / 3 + x1;
var y3 = (y2 - y1) /3 + y1;
var x4 = (x2 - x1) / 3 * 2 + x1;
var y4 = (y2 - y1) / 3 * 2 + y1;
var x5 = x3 + ((x2 - x1) - (y2 - y1) * Math.sqrt(3)) / 6;
var y5 = y3 + ((x2 - x1) * Math.sqrt(3) + (y2 - y1)) / 6;
n = n + 1;
if(n == m){
ctx.moveTo(x1, y1);
ctx.lineTo(x3, y3);
ctx.lineTo(x5, y5);
ctx.lineTo(x4, y4);
ctx.lineTo(x2, y2);
ctx.stroke();
return false;
}
koch(ctx, x1, y1, x3, y3, n, m)
koch(ctx, x3, y3, x5, y5, n, m)
koch(ctx, x5, y5, x4, y4, n, m)
koch(ctx, x4, y4, x2, y2, n, m)
}
只要说明参数的意思,代码应该是不需要注释了,很简单。下面加入draw方法,用来执行绘制: function draw(){
var canvas = document.getElementById("cantest");
if(canvas.getContext){
canvas.height = canvas.height;
var ctx = canvas.getContext("2d");
ctx.strokeStyle = "#fff";
ctx.beginPath();
var x1 = 400.00;
var y1 = 150.00;
var x2 = 100.00;
var y2 = 150.00;
var x11 = x2 + (x1 - x2) / 2;
var y11 = y1 + Math.sin(Math.PI / 3) * (x1 - x2);
var depth = parseInt(document.getElementById("txtDepth").value); //取得一个文本框的值,可以调整维度,这里没有进行输入判断。
koch(ctx, x1, y1, x2, y2, 0, depth);
koch(ctx, x11, y11, x1, y1, 0, depth);
koch(ctx, x2, y2, x11, y11, 0, depth);
}else{
alert("不支持Canvas");
}
}
var canvas = document.getElementById("cantest");
if(canvas.getContext){
canvas.height = canvas.height;
var ctx = canvas.getContext("2d");
ctx.strokeStyle = "#fff";
ctx.beginPath();
var x1 = 400.00;
var y1 = 150.00;
var x2 = 100.00;
var y2 = 150.00;
var x11 = x2 + (x1 - x2) / 2;
var y11 = y1 + Math.sin(Math.PI / 3) * (x1 - x2);
var depth = parseInt(document.getElementById("txtDepth").value); //取得一个文本框的值,可以调整维度,这里没有进行输入判断。
koch(ctx, x1, y1, x2, y2, 0, depth);
koch(ctx, x11, y11, x1, y1, 0, depth);
koch(ctx, x2, y2, x11, y11, 0, depth);
}else{
alert("不支持Canvas");
}
}
运行效果如图1-4: 
图1-4 PS:维度到6就相当吃内存,建议取不大于5的维度测试,不然浏览器容易卡死。有机会用桌面程序试验下更高维度的样子。




