不动点迭代法和牛顿迭代法

不定点迭代法

方程的根

不动迭代法的概念

代码实现

import numpy
import numpy as np
from sympy import *
import math
import matplotlib.pyplot as plt
from sympy.simplify.fu import L


def detfunction(x):

    return pow((x+1), 1/3)


def erfen(point1, point2, min_area):

    min = point1
    max = point2
    isquit = True
    while isquit:
        mid = point1+1/2*(point2-point1)
        if detfunction(mid) * detfunction(min) <= 0:
            max = mid
        elif detfunction(mid)*detfunction(max) < 0:
            min = mid
        if(math.fabs(max-min) < min_area):
            isquit = False
    return min, max


def calu_result(accuary, point):

    minarea = 1
    # erfen()
    isquit = True
    first = point
    count = 0       #次数
    while isquit:
        # 计算结果
        res = detfunction(first)
        if(abs(first-res) < accuary):
            first = res
            isquit = False
        first = res
        count += 1
    return first, count


def draw(left, right):
    # x = np.arange(left-5,right+5,0.1)
    # x_v = x
    # y = []
    # for i in range(len(x)):
    #     res =detfunction(x[i])
    #     y.append(res)
    # plt.plot(x,x_v,label = "y=x")
    # plt.plot(x,y,label = "y = (x+1)^1/3")
    # # ax = gca()
    # plt.show()

    plt.figure(figsize=(12, 8), dpi=72)
    plt.subplot(1, 1, 1)
    X = np.linspace(-10,10, 2048, endpoint=True)
    X_val = X
    Y_val = np.zeros(len(X))
    for i in range(len(X)):
        res = detfunction(X[i])
        Y_val[i] = res
        
    plt.plot(X, X_val, linewidth=1.5, linestyle="-", label="y =x")
    plt.plot(X, Y_val, linewidth=1.5, linestyle="-", label="y =(x+1)^1/3")
    plt.legend(loc='upper left')
    plt.xlim(-4.5, 4.5)
    # 设置纵轴的上下限
    plt.ylim(-4.5, 4.5)

    # 设置纵轴记号
    plt.yticks(np.linspace(-1, 1, 5, endpoint=True))
    ax = plt.gca()
    ax.spines['right'].set_color('none')
    ax.spines['top'].set_color('none')
    ax.xaxis.set_ticks_position('bottom')
    ax.spines['bottom'].set_position(('data', 0))
    ax.yaxis.set_ticks_position('left')
    ax.spines['left'].set_position(('data', 0))

    # savefig("sincosin.png",dpi=72) #以72dpi保存图像
    plt.show()

point = float(input("请输入迭代法的初始值"))
accuary = float(input("请输入最大允许误差值"))
res, count = calu_result(accuary, point)
print(f"结果：{res}")
print(f"迭代次数：{count}")
ma = max(res, point)
small = min(res, point)
draw(small*0.8, ma*1.2)

实验样例

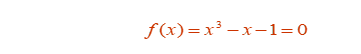
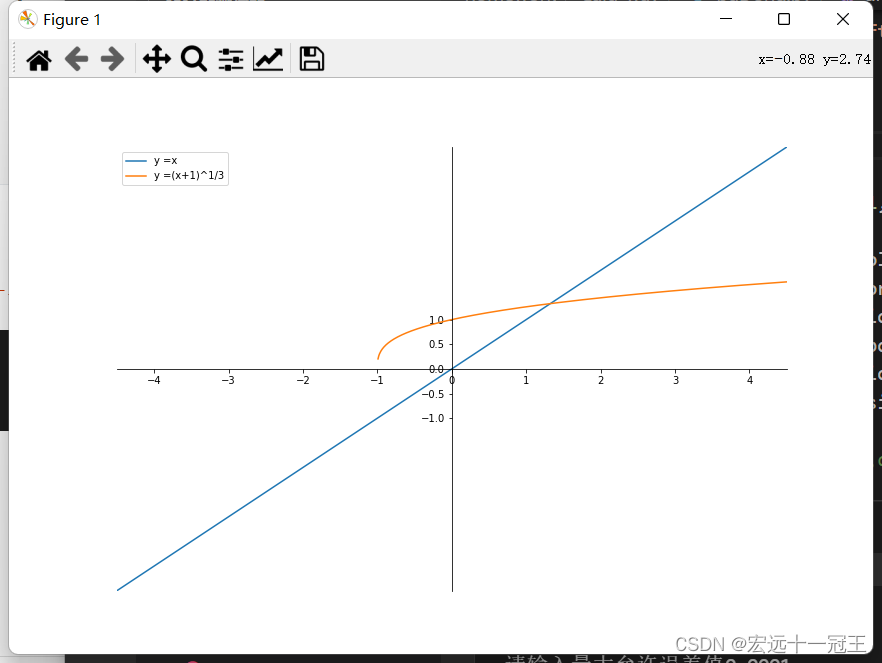
函数的图像

样例2

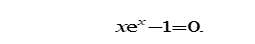
牛顿法、牛顿简化法，牛顿下山法

牛顿法

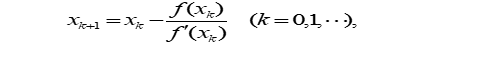
迭代函数

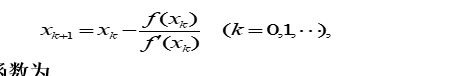
牛顿简化法

由于牛顿法计算导数时比较困难，就用写于为f（x0)的导数的平行弦与x轴的交点来替代

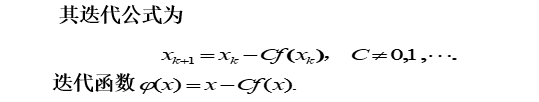
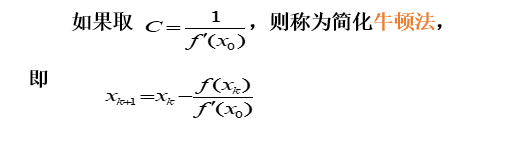
牛顿下山法

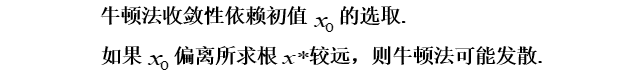
代码实现

牛顿法

def calu_result(diff_function,function,accuary,point,x):
    
    is_quit = True
    Init_first = point
    count =0	#次数
    while is_quit:
        res1 = function.subs(x,Init_first)
        res2 = diff_function.subs(x,Init_first)
        temp = Init_first-(res1/res2)	#每次迭代的xk
        if abs(temp-Init_first)<accuary:
            
            Init_first = temp	#更新xk
            count+=1
            return Init_first,count
        if(count>100):
            return temp,count
        Init_first = temp
        count+=1

牛顿简化法

def calu_Simple_result(diff_function,function,accuary,point,x):
    
    is_quit = True
    Init_first = point
    count =0	#次数
    res2 = diff_function.subs(x,Init_first)	#平行弦
    while is_quit:
        res1 = function.subs(x,Init_first)
        temp = Init_first-(res1/res2)
        if abs(temp-Init_first)<accuary:
            
            Init_first = temp
            count+=1
            return Init_first,count
        if(count>100):
            return temp,count
        Init_first = temp
        count+=1

牛顿下山法

def mountain_result(diff_function,function,accuary,point,x):
    is_quit = True
    Init_first = point
    second =point
    count =0
    weight = 1
    is_mul = False
   #计算下山因子
    while is_quit!=False:
        res1 = function.subs(x,second)
        res2 = diff_function.subs(x,second)
        temp = second-(res1/res2)
        if abs(detfunction(temp))-abs(detfunction(second)) <0:
            break
            #每次减半，直到合适的下山因子
        weight  = weight/2
        second = temp
    # print(weight)
    
    while is_quit:
        #根据下山因子计算
        res1 = function.subs(x,Init_first)
        res2 = diff_function.subs(x,Init_first)
        temp = Init_first - weight*(res1/res2)
        if abs(temp-Init_first)<accuary:
            Init_first = temp
            return Init_first,count,weight
          #设定一个，100轮还没有结束，也退出，相当于一个最大迭代次数
        if(count>100):
            return temp,count,weight
        Init_first = temp
        count+=1

三种方法实验结果

样例1

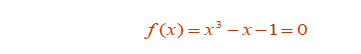
第一行为求导后的表达式，后面的为迭代次数和结果

当取初值为0.6时，应该可能出现，离根比较远的情况，此时牛顿法收敛法比较慢，而牛顿简化法已经不满足收敛条件了，而牛顿下山法可以保证它的收敛性，慢慢逼近根

全部代码

不动点迭代法

import numpy
import numpy as np
from sympy import *
import math
import matplotlib.pyplot as plt
from sympy.simplify.fu import L


def detfunction(x):

    return 1/exp(x)


def erfen(point1, point2, min_area):

    min = point1
    max = point2
    isquit = True
    while isquit:
        mid = point1+1/2*(point2-point1)
        if detfunction(mid) * detfunction(min) <= 0:
            max = mid
        elif detfunction(mid)*detfunction(max) < 0:
            min = mid
        if(math.fabs(max-min) < min_area):
            isquit = False
    return min, max


def calu_result(accuary, point):

    minarea = 1
    # erfen()
    isquit = True
    first = point
    count = 0       #次数
    while isquit:
        # 计算结果
        res = detfunction(first)
        if(abs(first-res) < accuary):
            first = res
            isquit = False
        first = res
        count += 1
    return first, count


def draw(left, right):
    # x = np.arange(left-5,right+5,0.1)
    # x_v = x
    # y = []
    # for i in range(len(x)):
    #     res =detfunction(x[i])
    #     y.append(res)
    # plt.plot(x,x_v,label = "y=x")
    # plt.plot(x,y,label = "y = (x+1)^1/3")
    # # ax = gca()
    # plt.show()

    plt.figure(figsize=(12, 8), dpi=72)
    plt.subplot(1, 1, 1)
    X = np.linspace(-10,10, 2048, endpoint=True)
    X_val = X
    Y_val = np.zeros(len(X))
    for i in range(len(X)):
        res = detfunction(X[i])
        Y_val[i] = res
        
    plt.plot(X, X_val, linewidth=1.5, linestyle="-", label="y =x")
    plt.plot(X, Y_val, linewidth=1.5, linestyle="-", label="y =1/e^x")
    plt.legend(loc='upper left')
    plt.xlim(-4.5, 4.5)
    # 设置纵轴的上下限
    plt.ylim(-4.5, 4.5)

    # 设置纵轴记号
    plt.yticks(np.linspace(-1, 1, 5, endpoint=True))
    ax = plt.gca()
    ax.spines['right'].set_color('none')
    ax.spines['top'].set_color('none')
    ax.xaxis.set_ticks_position('bottom')
    ax.spines['bottom'].set_position(('data', 0))
    ax.yaxis.set_ticks_position('left')
    ax.spines['left'].set_position(('data', 0))

    # savefig("sincosin.png",dpi=72) #以72dpi保存图像
    plt.show()

point = float(input("请输入迭代法的初始值"))
accuary = float(input("请输入最大允许误差值"))
res, count = calu_result(accuary, point)
print(f"结果：{res}")
print(f"迭代次数：{count}")
ma = max(res, point)
small = min(res, point)
draw(small*0.8, ma*1.2)

牛顿迭代法

import numpy
import numpy as np
from sympy import *
import math
import matplotlib.pyplot as plt
from sympy.simplify.fu import L


def draw(left, right):
    # x = np.arange(left-5,right+5,0.1)
    # x_v = x
    # y = []
    # for i in range(len(x)):
    #     res =detfunction(x[i])
    #     y.append(res)
    # plt.plot(x,x_v,label = "y=x")
    # plt.plot(x,y,label = "y = (x+1)^1/3")
    # # ax = gca()
    # plt.show()

    plt.figure(figsize=(12, 8), dpi=72)
    plt.subplot(1, 1, 1)
    X = np.linspace(-10,10, 2048, endpoint=True)
    X_val = X
    Y_val = np.zeros(len(X))
    for i in range(len(X)):
        res = detfunction(X[i])
        Y_val[i] = res
        
    plt.plot(X, X_val, linewidth=1.5, linestyle="-", label="y =x")
    plt.plot(X, Y_val, linewidth=1.5, linestyle="-", label="y =(x+1)^3-x-1")
    plt.legend(loc='upper left')
    plt.xlim(-4.5, 4.5)
    # 设置纵轴的上下限
    plt.ylim(-4.5, 4.5)

    # 设置纵轴记号
    plt.yticks(np.linspace(-1, 1, 5, endpoint=True))
    ax = plt.gca()
    ax.spines['right'].set_color('none')
    ax.spines['top'].set_color('none')
    ax.xaxis.set_ticks_position('bottom')
    ax.spines['bottom'].set_position(('data', 0))
    ax.yaxis.set_ticks_position('left')
    ax.spines['left'].set_position(('data', 0))

    # savefig("sincosin.png",dpi=72) #以72dpi保存图像

    # 在屏幕上显示
    plt.show()
    
def getdiff(function,x):
    
    return diff(function,x)
    
def detfunction(x):

    return pow(x,3)-x-1

def calu_Simple_result(diff_function,function,accuary,point,x):
    print("牛顿简化法")
    is_quit = True
    Init_first = point
    count =0
    res2 = diff_function.subs(x,Init_first)
    while is_quit:
        res1 = function.subs(x,Init_first)
        temp = Init_first-(res1/res2)
        print(f"第{count}的值{temp}")
        if abs(temp-Init_first)<accuary:
            
            Init_first = temp
            count+=1
            return Init_first,count
        if(count>100 or abs(temp-Init_first)>100000):
            return temp,count
        Init_first = temp
        count+=1

def calu_result(diff_function,function,accuary,point,x):
    print("牛顿法")
    is_quit = True
    Init_first = point
    count =0    
    while is_quit:
        res1 = function.subs(x,Init_first)
        res2 = diff_function.subs(x,Init_first)
        temp = Init_first-(res1/res2)
        print(f"第{count}的值：{temp}")
        if abs(temp-Init_first)<accuary:
            
            Init_first = temp
            count+=1
            return Init_first,count
        if(count>100):
            return temp,count
        Init_first = temp
        count+=1

def mountain_result(diff_function,function,accuary,point,x):
    print("牛顿下山法")
    is_quit = True
    Init_first = point
    second =point
    count =0
    weight = 1
    is_mul = False
    while is_quit!=False:
        res1 = function.subs(x,second)
        res2 = diff_function.subs(x,second)
        temp = second-(res1/res2)
        if abs(detfunction(temp))-abs(detfunction(second)) <0:
            break
        weight  = weight/2
        second = temp
    # print(weight)
    
    while is_quit:
        res1 = function.subs(x,Init_first)
        res2 = diff_function.subs(x,Init_first)
        temp = Init_first - weight*(res1/res2)
        print(f"第{count}的值{temp}")
        if abs(temp-Init_first)<accuary:
            Init_first = temp
            return Init_first,count,weight
            
        if(count>100):
            return temp,count,weight
        Init_first = temp
        count+=1
    
x = symbols('x')
function = detfunction(x)
diff_function = getdiff(function,x)
print(diff_function)
point = float(input("请输入迭代法的初始值"))
accuary = float(input("请输入最大允许误差值"))
res, count = calu_result(diff_function,function,accuary, point,x)
res2,count2 = calu_Simple_result(diff_function,function,accuary, point,x)
res3,count3,weight = mountain_result(diff_function,function,accuary, point,x)
if count!=100:
    print(f"牛顿法结果：{res}")
    print(f"迭代次数：{count}")
# else:
#     print(f"迭代次数：{count}")
#     print(f"牛顿法结果：{res},达到最大迭代次数")
    
if count2!=100:
    print(f"牛顿简化法结果：{res2}")
    print(f"迭代次数：{count2}")
# else:
#     print(f"牛顿简化法结果：{res2}")
#     print(f"迭代次数：{count2},达到最大迭代次数")
    
if count3!=100:
    print("下山因子为：{}".format(weight))
    print(f"牛顿下山法结果：{res3}")
    print(f"迭代次数：{count3}")
ma = max(res, point)
small = min(res, point)
draw(small*0.8, ma*1.2)

总结

本文是学习的一些笔记，创作不易，点个爱心是缘分，不点是本分，如果有问题可以私信或者在下面评论，大家可以一起学习！！！