CV 光流场计算2( L-K方法 )
在计算机视觉中,卢卡斯-卡纳德方法是一种广泛使用的光流估计的差分方法,这个方法是由Bruce D. Lucas和Takeo Kanade发明的。它假设光流在像素点的邻域是一个常数,然后使用最小二乘法对邻域中的所有像素点求解基本的光流方程。
通过结合几个邻近像素点的信息,卢卡斯-卡纳德方法(简称为L-K方法)通常能够消除光流方程里的多义性。而且,与逐点计算的方法相比,L-K方法对图像噪声不敏感。不过,由于这是一种局部方法,所以在图像的均匀区域内部,L-K方法无法提供光流信息。
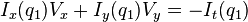
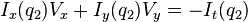

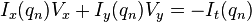
其中,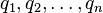 是窗口中的像素,
是窗口中的像素,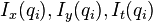 是图像在点
是图像在点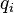 和当前时间对位置x,y和时间t的偏导。
和当前时间对位置x,y和时间t的偏导。
这些等式可以写成矩阵的形式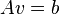 ,此处
,此处
![A = \begin{bmatrix} I_x(q_1) & I_y(q_1) \\[10pt] I_x(q_2) & I_y(q_2) \\[10pt] \vdots & \vdots \\[10pt] I_x(q_n) & I_y(q_n) \end{bmatrix}, \quad\quad v = \begin{bmatrix} V_x\\[10pt] V_y \end{bmatrix}, \quad \mbox{and}\quad b = \begin{bmatrix} -I_t(q_1) \\[10pt] -I_t(q_2) \\[10pt] \vdots \\[10pt] -I_t(q_n) \end{bmatrix}](http://upload.wikimedia.org/math/3/3/e/33ec519f1943a440783c93b4ac98b4a4.png)
此方程组的等式个数多于未知数个数,所以它通常是超定的。L-K方法使用最小二乘法获得一个近似解,即计算一个2x2的方程组:
![A^T A v=A^T b]() 或
或![\mathrm{v}=(A^T A)^{-1}A^T b]()
其中, 是矩阵
是矩阵 的转置。即计算:
的转置。即计算:
![\begin{bmatrix} V_x\\[10pt] V_y \end{bmatrix} = \begin{bmatrix} \sum_i I_x(q_i)^2 & \sum_i I_x(q_i)I_y(q_i) \\[10pt] \sum_i I_y(q_i)I_x(q_i) & \sum_i I_y(q_i)^2 \end{bmatrix}^{-1} \begin{bmatrix} -\sum_i I_x(q_i)I_t(q_i) \\[10pt] -\sum_i I_y(q_i)I_t(q_i) \end{bmatrix}](http://upload.wikimedia.org/math/7/6/1/76131d763130942b287208d7378bcf5f.png)
对i=1 到 n求和。
矩阵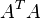 通常被称作图像在点p的 结构张量。
通常被称作图像在点p的 结构张量。

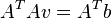 或
或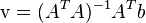

 浙公网安备 33010602011771号
浙公网安备 33010602011771号