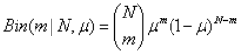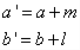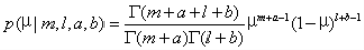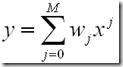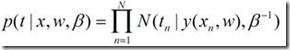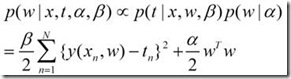贝叶斯、概率分布与机器学习
本文由LeftNotEasy原创,可以转载,但请保留出处和此行,如果有商业用途,请联系作者 wheeleast@gmail.com
一. 简单的说贝叶斯定理:
贝叶斯定理用数学的方法来解释生活中大家都知道的常识
形式最简单的定理往往是最好的定理,比如说中心极限定理,这样的定理往往会成为某一个领域的理论基础。机器学习的各种算法中使用的方法,最常见的就是贝叶斯定理。
贝叶斯定理的发现过程我没有找到相应的资料,不过我相信托马斯.贝叶斯(1702-1761)是通过生活中的一些小问题去发现这个对后世影响深远的定理的,而且我相信贝叶斯发现这个定理的时候,还不知道它居然有这么大的威力呢。下面我用一个小例子来推出贝叶斯定理:
已知:有N个苹果,和M个梨子,苹果为黄色的概率为20%,梨子为黄色的概率为80%,问,假如我在这堆水果中观察到了一个黄色的水果,问这个水果是梨子的概率是多少。
用数学的语言来表达,就是已知P(apple) = N / (N + M), P(pear) = M / (N + M), P(yellow|apple) = 20%, P(yellow|pear) = 80%, 求P(pear|yellow).
要想得到这个答案,我们需要 1. 要求出全部水果中为黄色的水果数目。 2. 求出黄色的梨子数目
对于1) 我们可以得到 P(yellow) * (N + M), P(yellow) = p(apple) * P(yellow|apple) + P(pear) * p(yellow|pear)
对于2) 我们可以得到 P(yellow|pear) * M
2) / 1) 可得:P(pear|yellow) = P(yellow|pear) * p(pear) / [P(apple) * P(yellow|apple) + P(pear) * P(yellow|pear)]
化简可得:P(pear|yellow) = P(yellow,pear) / P(yellow), 用简单的话来表示就是在已知是黄色的,能推出是梨子的概率P(pear|yellow)是黄色的梨子占全部水果的概率P(yellow,pear)除上水果颜色是黄色的概率P(yellow). 这个公式很简单吧。
我们将梨子代换为A,黄色代换为B公式可以写成:P(A|B) = P(A,B) / P(B), 可得:P(A,B) = P(A|B) * P(B).贝叶斯公式就这样推出来了。
本文的一个大概的思路:先讲一讲我概括出的一个基本的贝叶斯学习框架,然后再举几个简单的例子说明这些框架,最后再举出一个复杂一点的例子,也都是以贝叶斯机器学习框架中的模块来讲解
二. 贝叶斯机器学习框架
对于贝叶斯学习,我每本书都有每本书的观点和讲解的方式方法,有些讲得很生动,有些讲得很突兀,对于贝叶斯学习里面到底由几个模块组成的,我一直没有看到很官方的说法,我觉得要理解贝叶斯学习,下面几个模块是必须的:
1) 贝叶斯公式
机器学习问题中有一大类是分类问题,就是在给定观测数据D的情况下,求出其属于类别(也可以称为是假设h,h ∈ {h0, h1, h2…})的概率是多少, 也就是求出:
P(h|D), 可得:
P(h,D) = P(h|D) * P(D) = P(D|h) * P(h), 所以:P(h|D) = P(D|h) * P(h) / P(D), 对于一个数据集下面的所有数据,P(D),恒定不变。所以可以认为P(D)为常数, 得到:P(h|D) ∝ P(D|h) * P(h)。我们往往不用知道P(h|D)的具体的值,而是知道例如P(h1|D),P(h2|D)值的大小关系就是了。这个公式就是机器学习中的贝叶斯公 式,一般来说我们称P(h|D)为模型的后验概率,就是从数据来得到假设的概率,P(h)称为先验概率,就是假设空间里面的概率,P(D|h)是模型的 likelihood概率。
Likelihood(似然)这个概率比较容易让人迷惑,可以认为是已知假设的情况下,求出从假设推出数据的概率,在实际的机器学习过程中,往往加入了很多的假设,比如一个英文翻译法文的问题:
给出一个英文句子,问哪一个法文句子是最靠谱的,P(f=法文句子|e=英文句子) = P(e|f) * p(f), p(e|f)就是likelihood函数,P(e|f) 写成下面的更清晰一点:p(e|f∈{f1,f2…})可以认为,从输入的英文句子e,推出了很多种不同的法文句子f,p(e|f)就是从这些法文句子中的某一个推出原句子e的概率。
本文之后的内容也将对文章中没有提到的一些内容,也是贝叶斯学习中容易疑惑、忽略、但是很重要的问题进行一些解释。
2) 先验分布估计,likelihood函数选择
贝叶斯方法中,等号右边有两个部分,先验概率与likelihood函数。先验概率是得到,在假设空间中,某一个假设出现的概率是多少,比如说在街上看到一个动物是长有毛的,问1. 这个动物是哈巴狗的概率是多少,2. 这个动物是爪哇虎的概率是多少, 见下图:
虽然两个假设的likelihood函数都非常的接近于1(除非这个动物病了),但是由于爪哇虎已经灭绝了,所以爪哇虎的先验概率为0,所以P(爪哇虎|有毛的动物)的概率也为0。
先验概率分布估计
在观测的时候,对于变量是连续的情况下,往往需要一个先验分布来得到稀疏数据集中没有出现过的,给出的某一个假设,在假设空间中的概率。比如说有一个很大很大的均匀金属圆盘,问这个金属圆盘抛到空中掉下来,正面朝上的概率,这个实验的成本比较高(金属圆盘又大又重),所以只能进行有限次数的实验,可能出现的是,正面向上4次,反面向上1次,但是我们如果完全根据这个数据集去计算先验概率,可能会出现很大的偏差。不过由于我们已知圆盘是均匀的,我们可以根据这个知识,假设P(X=正面) = 0.5。
我们有的时候,已知了分布的类型,但是不知道分布的参数,还需要根据输入的数据,对分布的参数进行估计、甚至对分布还需要进行一些修正,以满足我们算法的需求:比如说我们已知某一个变量x的分布是在某一个连续区间均匀分布,我们观察了1000次该变量,从小到大排序结果是:1,1.12,1.5 … 199.6, 200, 那我们是否就可以估计变量的分布是从[1,200]均匀分布的?如果出现一个变量是0.995,那我们就能说P(0.995) = 0?如果出现一个200.15怎么办呢?所以我们这个时候可能需要对概率的分布进行一定的调整,可能在x<1,x>200的范围内的概率是一个下降的直线,整个概率密度函数可能是一个梯形的,或者对区域外的值可以给一个很小很小的概率。这个我在之后还将会举出一些例子来说明。
Likelihood函数选择
对于同一个模型,likelihood函数可能有不同的选择,对于这些选择,可能有些比较精确、但是会搜索非常大的空间,可能有些比较粗糙,但是速度会比较快,我们需要选择不同的likelihood函数来计算后验概率。对于这些Likelihood函数,可能还需要加上一些平滑等技巧来使得最大的降低数据中噪声、或者假设的缺陷对结果的影响。
我所理解的用贝叶斯的方法来估计给定数据的假设的后验概率,就是通过prior * likelihood,变换到后验分布。是一个分布变换的过程。
3) loss function(损失函数)
x是输入的数据,y(x)是推测出的结果的模型,t是x对应的真实结果,L(t,y(x))就是loss function,E[L]表示使用模型y进行预测,使用L作为损失函数的情况下,模型的损失时多少。通常来说,衡量一个模型是否能够准确的得到结果,损失函数是最有效的一个办法,最常用、最简单的一种损失函数是:
不过我一直不知道为什么这里用的平方,而不是直接用绝对值,有详细一点的解释吗?:-p
4) Model Selection(模型选择)
前文说到了对于likelihood函数可以有不同的选择,对于先验的概率也可以有不同的选择,不过假设我们一个构造完整的测试集和一个恰当的损失函数,最终的结果将会是确定的,量化的,我们很容易得到两个不同参数、方法的模型的优劣性。不过通常情况下,我们的测试集是不够完整,我们的损失函数也是不那么 的精确,所以对于在这个测试集上表现得非常完美的模型,我们常常可能还需要打一个问号,是否是训练集和测试集过于相像,模型又过于复杂。导致了over-fitting(后文将会详细介绍over-fitting的产生)?
Model Selection本质上来说是对模型的复杂度与模型的准确性做一个平衡,本文后面将有一些类似的例子。
Example 1:Sequential 概率估计
注:此例子来自PRML chapter 2.1.1
对于概率密度的估计,有很多的方法,其中一种方法叫做Sequential 概率估计。
这种方法是一个增量的学习过程,在每看到一个样本的时候都是把之前观测的数据作为先验概率,然后在得到新数据的后验概率后,再把当前的后验概率作为下一次预测时候的先验概率。
传统的二项式分布是:
由于传统的二项式分布的概率μ是完全根据先验概率而得到的,而这个先验分布之前也提到过,可能会由于实验次数不够而有很大的偏差,而且,我们无法得知μ的分布,只知道一个μ的期望,这样对于某些机器学习的方法是不利的。为了减少先验分布对μ的影响,获取μ的分布,我们加入了两个参数,a,b,表示X=0与X=1的出现的次数,这个取值将会改变μ的分布,beta分布的公式如下:
对于不同a,b的取值,将会对μ的概率密度函数产生下面的影响:(图片来自PRML)
在观测数据的过程中,我们可以随时的利用观测数据的结果,改变当前μ的先验分布。我们可以将Beta分布加入两个参数,m,l,表示观测到的X=0,X=1的次数。(之前的a,b是一个先验的次数,不是当前观测到的)
我们令:
a’,b’表示加入了观测结果的新的a,b 。带入原式,可以得到
我们可以利用观测后的μ后验概率更新μ的先验概率,以进行下一次的观测,这样对不时能够得到新的数据,并且需要real-time给出结果的情况下很有用。不过Sequential方法有对数据一个i.i.d(独立同分布)的假设。要求每次处理的数据都是独立同分布的。
Example 2:拼写检查
这篇文章的中心思想来自:怎样写一个拼写检查器,如果有必要,请参见原文,本例子主要谈谈先验分布对结果的影响。
直接给出拼写检查器的贝叶斯公式:
P(c|w)表示,单词w(wrong)正确的拼写为单词c(correct)的概率,P(w|c)表示likelihood函数,在这里我们就简单的认 为,两个单词的编辑距离就是它们之间的likelihood,P(c)表示,单词c在整体文档集合中的概率,也就是单词c的先验概率。
我们在做单词拼写检查的时候肯定会直观的考虑:如果用户输入的单词如果在字典中没有出现过,则应该将其修正为一个字典中出现了的,而且与用户输入最接近的词;如果用户输入的词在字典中出现过了,但是词频非常的小,则我们可以为用户推荐一个比较接近这个单词,但是词频比较高的词。
先验概率P(c)的统计是一个很重要的内容,一般来说有两种可行的办法,一种是利用某些比较权威的词频字典,一种是在自己的语料库(也就是待进行拼写检查的语料)中进行统计。我建议是用后面的方法进行统计,这样词的先验概率才会与测试的环境比较匹配。比如说一个游戏垂直搜索网站需要对用户输入的信息进行拼写纠正,那么使用通用环境下统计出的先验概率就不太适用了。
Example 3:奥卡姆剃刀与Model Selection
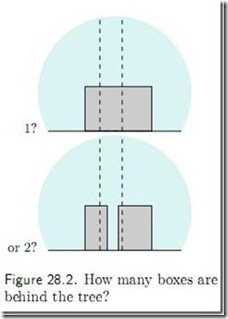
给出下面的一个图:(来自Mackey的书)
问:大树背后有多少个箱子?
其实,答案肯定是有很多的,一个,两个,乃至N箱子都是有可能的(比如说后面有一连排的箱子,排成一条直线),我们只能看到第一个:
但是,最正确,也是最合理的解释,就是一个箱子,因为如果大树背后有两个乃至多个箱子,为什么从大树正面看起来,两边的高度一样,颜色也一样,这样是不是太巧合了。如果我们的模型根据这张图片,告诉我们大树背后最有可能有两个箱子,这样的模型的泛化能力是不是太差了。
所以说,本质上来说,奥卡姆剃刀,或者模型选择,也是人生活中的一种通常行为的数学表示,是一种化繁为简的过程。数学之美番外篇:平凡而又神奇的贝叶斯方法这篇文章中说的,奥卡姆剃刀工作在likelihood上,对于模型的先验分布并没有什么影响。我这里不太同意这个说法:奥卡姆剃刀是剪掉了复杂的模型,复杂的模型也是不常见的、先验概率比较低的,最终的结果是选择了先验概率比较高的模型。
Example 4: 曲线拟合:
(该例子来自PRML)
问题:给定一些列的点,x = {x1,x2...xn}, t = {t1,t2 .. tn}, 要求用一个模型去拟合这个观测,能够使得给定一个新点x', 能够给出一个t'.
已知给定的点是由y=2πx加上正态分布的噪声而得到的10个点,如上图。为了简单起见,我们用一个多项式去拟合这条曲线:
为了验证我们的公式是否正确,我们加入了一个loss function:
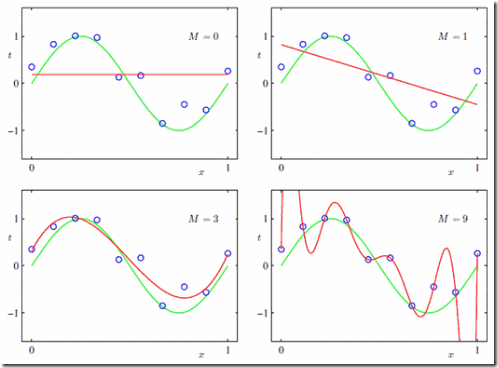
在loss function最小的情况下,我们绘制了不同维度下多项式生成的曲线:
在M值增高的情况下,曲线变得越来越陡峭,当M=9的时候,该曲线除了可以拟合输入样本点外,对新进来的样本点已经无法预测了。我们可以观测一下多项式的系数:
可以看出,当M(维度)增加的时候,系数也膨胀得很厉害,为了消除这个系数带来的影响,我们需要简化模型,我们为loss function加入一个惩罚因子:
我们把w的L2距离乘上一个系数λ加入新的loss function中,这就是一个奥卡姆剃刀,把原本复杂的系数变为简单的系数(如果要更具体的量化的分析,请见PRML 1.1节)。如果我们要考虑如何选择最合适的维度,我们也可以把维度作为一个loss function的一部分,这就是Model Selection的一种。
但是这个问题还没有解决得很好,目前我们得到的模型只能预测出一个准确的值:输入一个新的x,给出一个t,但是不能描述t有什么样的概率密度函数。概率密度函数是很有用的。假如说我们的任务修正为,给出N个集合,每个集合里面有若干个点,表示一条曲线,给出一个新的点,问这个新的点最可能属于哪一条曲线。如果我们仅仅用新的点到这些曲线的距离作为一个衡量标准,那很难得到一个比较有说服力的结果。为了能够获取t值的一个分布,我们不妨假设t属于一个均值为y(x),方差为1/β的一个高斯分布:
在之前的E(w),我们加入了一个w的L2距离,这个看起来有一点突兀的感觉,为什么要加上一个这样的距离呢?为什么不是加入一个其他的东西。我们可以用一个贝叶斯的方法去替代它,得到一个更有说服力的结果。我们令p(w)为一个以0为均值,α为方差的高斯分布,这个分布为w在0点附近密度比较高,作为w的先验概率,这样在计算最大化后验概率的时候,w的绝对值越小,后验概率将会越大。
我们可以得到新的后验概率:
这个式子看起来是不是有点眼熟啊?我们令λ=α/β,可以得到类似于之前损失函数的一个结果了。我们不仅还是可以根据这个函数来计算最优的拟合函数,而且可以得到相应的一个概率分布函数。可以为机器学习的很多其他的任务打下基础。
这里还想再废话一句,其实很多机器学习里面的内容都与本处所说的曲线拟合算法类似,如果我们不用什么概率统计的知识,可以得到一个解决的方案,就像我们的第一个曲线拟合方案一样,而且还可以拟合得很好,不过唯一缺少的就是概率分布,有了概率分布可以做很多的事情。包括分类、回归等等都需要这些东西。从本质上来说,Beta分布和二项式分布,Dirichlet分布和多项式分布,曲线拟合中直接计算w和通过高斯分布估计w,都是类似的关系:Beta分布和Dirichlet分布提供的是μ的先验分布。有了这个先验分布,我们可以去更好的做贝叶斯相关的事情。
后记:
本文就写到这里,花了大概4个晚上来写这篇文章,也感谢我女朋友的支持。我也希望能够用它去总结一下最近学习的一些心得,看看是否自己能够把它讲出来。我觉得学习的过程是一个爬山的过程,常常有的时候觉得自己快到山峰了,结果路有向下了,自己不停有着挫折和兴奋的感觉,不过学习的感觉总体来说快乐的。我也想能够把自己的这份快乐带给大家 :-D
参考资料:
数学之美番外篇:平凡而又神奇的贝叶斯方法, Pongba
Pattern Recognition and Machine Learning, Bishop
一些Wikipedia上面的内容