6D姿态估计从0单排——看论文的小鸡篇——Deep Learning of Local RGB-D Patches for 3D Object Detection and 6D Pose Estimation
we employ a convolutional auto-encoder that has been trained on a large collection of random local patches. We demonstrate that neural networks coupled with a local voting-based approach can be used to perform reliable 3D object detection and pose estimation under clutter and occlusion. To this end, we deeply learn descriptive features from local RGB-D patches and use them afterwards to create hypotheses in the 6D pose space.
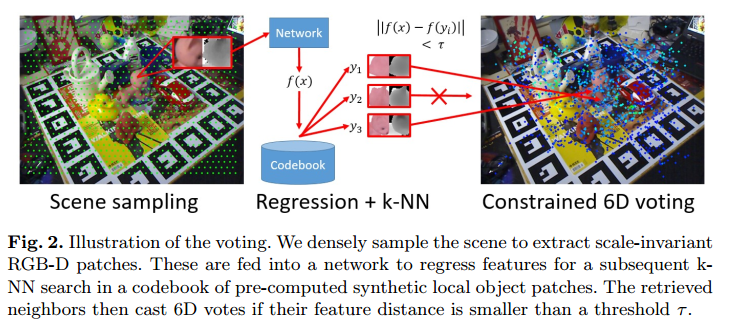
we train a convolutional autoencoder (CAE) from scratch using random patches from RGB-D images with the goal of descriptor regression. With this network we create codebooks from synthetic patches sampled from object views where each codebook entry holds a local 6D pose vote. In the detection phase we sample patches in the input image on a regular grid, compute their descriptors and match them against codebooks with an approximate k-NN search.

- Local Patch Representation: Given an object appearance, the idea is to separate it into its local parts and let them vote independently. To represent an object locally, we render it from many viewpoints sampled on an icosahedron, and densely extract a set of scale-independent RGB-D patches. we take depth z at the patch center point and compute the patch pixel size such that the patch corresponds to a fixed metric size m :\(patch_{size} = \frac{m}{z}\cdot f\) with f being the focal length of the rendering camera. we de-mean the depth values with z and clamp them to \(\pm m\) to confine the patch locally not only along x and y, but also along z. Finally, we normalize color and depth to \([−1, 1]\) and resize the patches to \(32\times 32\). Our method instead does not need to model the background at all.
- Network Training: we decided to train from scratch(从头开始) due to multiple reasons:
- Not many works have incorporated depth as an additional channel, depth noise
- first to focus on local RGB-D patches of small-scale objects
- To robustly train deep architectures, a high amount of training samples is needed.
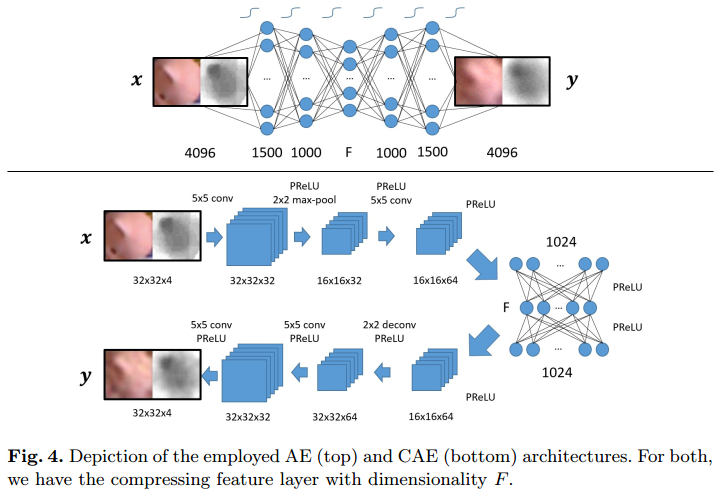
We randomly sample local patches from the LineMOD dataset. Furthermore, these samples were augmented such that each image got randomly flipped and its color channels permutated. Our network aims to learn a mapping from the high-dimensional patch space to a much lower feature space of dimensionality \(F\), and we employ a autoencoder (AE) and a convolutional autoencoder (CAE) to accomplish this task.
![]()
- Constrained Voting: A problem that is often encountered in regression tasks is the unpredictability of output values. In our case, this can be caused by unseen object parts, general background appearance or sensor noise in color or depth. we render an object from many views and store local patches y of this synthetic data in a database. For each \(y\), we compute its feature \(f(y)\in \mathbb{R}^F\) and store it together with a local vote \((t_x,t_y,t_z,\alpha,\beta,\gamma)\) describing the patch 3D center point offset to the object centroid and the rotation with respect to the local object coordinate frame.we take each sampled 3D scene point \(s = (s_x, s_y, s_z)\) with associated patch \(x\), compute its deep-regressed feature \(f(x)\) and retrieve k (approximate) nearest neighbors \(y_1,..., y_k\). Each neighbor casts then a global vote \(v(s,y) = (t_x + s_x, t_y + s_y, t_z + t_y, \alpha,\beta, \gamma)\) with an associated weight \(w(v) = e^{\left\|f(x)-f(y)\right\|}\) based on the feature distance.
![]()
Vote filtering: Casting votes can lead to a very crowded vote space that requires refinement in order to keep detection computationally feasible. We thus employ a three-stage filtering: in the first stage we subdivide the image plane into a 2D grid and throw each vote into the cell the projected centroid points to. We suppress all cells that hold less than k votes and extract local maxima after bilinear filtering over the accumulated weights of the cells. Each local mode collects the votes from its direct cell neighbors and performs mean shift with a flat kernel, first in translational and then in quaternion space.
![]()





 浙公网安备 33010602011771号
浙公网安备 33010602011771号