6D姿态估计从0单排——看论文的小鸡篇——Learning Descriptors for Object Recognition and 3D Pose Estimation
这篇文章和前一篇把神经网络主要集中于descriptor的对比方面不一样的是,这一篇中CNN还用来区分不同的物体类别和同类别不同姿态从而确保不同类间距较大同类间距较小(但是足以区分pose),这样就可以确保根据CNN对图片输入的输出值来直接确定对应的物体种类和其所应属于类别中的Pose,并且还采用了NN(nearest neighborhood)的办法去寻找最近的类别和姿态。
We train a CNN to compute these descriptors by enforcing simple similarity and dissimilarity constraints between the descriptors. both RGB and RGB-D data.
So far the only recognition approaches that have been demonstrated to work on large scale problems are based on Nearest Neighbor (NN) classification, because extremely efficient methods for NN search exist with an average complexity of \(O(1)\). Moreover, Nearest Neighbor (NN) classification also offers the possibility to trivially add new objects, or remove old ones.For NN approaches to perform well, a compact and discriminative description vector is required.
We seek to learn a descriptor with the two following properties: a) The Euclidean distance between descriptors from two different objects should be large; b) The Euclidean distance between descriptors from the same object should be representative of the similarity between their poses.
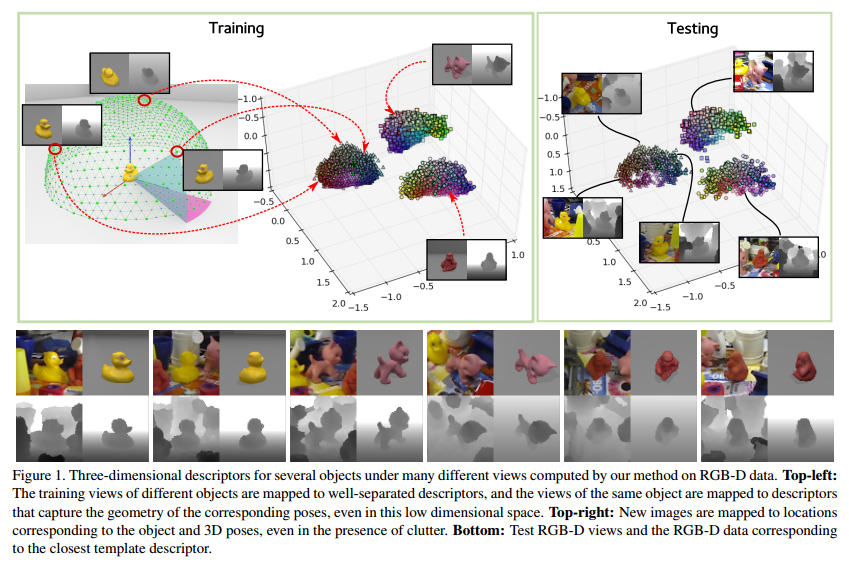
Given a new input image \(x\) of an object, we want to correctly predict the object's class and 3D pose.
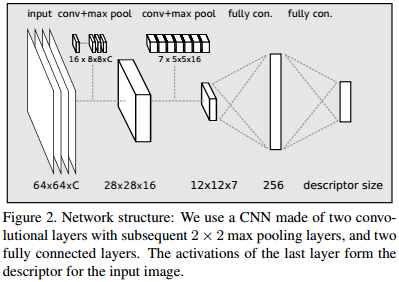
- Training the CNN: We need a set \(S_{train}\) of the training samples, where each sample \(s=(x,c,p)\) is made of an image \(x\) of an object, which can be a color or grayscale image or a depth map, or a combination of the two, the identity \(c\) of the object, the 3D pose \(p\) of the object relative to the camera. The set \(S_{db}\) of templates where each element is defined in the same way as a training samples. Descriptors for these templates are calculated and stored with the classifier for k-nearest neighbor search.
- Defining the Cost Function: We enforce these requirements by minimizing the following objective function over the parameters \(w\) of the CNN: \(L = L_{triplets}+L_{pairs}+\lambda\left\|w'\right\|^2_2\). The last term is a regularization term over the parameters of the network: \(w'\) denotes the vector made of all the weights of the convolutional filters and all nodes of the fully connect layers, except the bias terms.
Triplet-wise terms: A set \(T\) of triplets \((s_i,s_j,s_k)\) of training samples. Each triplet in \(T\) is selected such that one of the two following conditions is fulfilled: 1. \(s_i\) and \(s_j\) are from the same object and \(s_k\) from another object; 2. the three samples \(s_i\), \(s_j\) and \(s_k\) are from the same object, but the poses \(p_i\) and \(p_j\) are more similar than the poses \(p_i\) and \(p_k\). The triplets can therefore be seen as made of a pair of similar samples and a pair of dissimilar ones. We introduce a cost function for such a triplet: \(c(s_i,s_j,s_k)= \max(0,1-\frac{\left\|f_w(x_i)-f_w(x_k)\right\|_2}{\left\|f_w(x_i)-f_w(x_j)\right\|_2+m})\) where \(f_w(x)\) is the output of the CNN for an input image \(x\) and thus our descriptor for \(x\), and \(m\) is a margin. The sum of this cost function overall the triplets in \(T\):\(L_{triplets}=\sum_{(s_i,s_j,s_k)\in T}c(s_i,s_j,s_k)\)
Pair-wise terms: These terms make the descriptor robust to noise and other distracting artifacts such as changing illumination. We consider the set \(P\) of pairs \((s_i,s_j)\) of samples from the same object under very similar poses, ideally the same, and we define the \(L_{pairs}=\sum_{(s_i,s_j)\in P}\left\|f_w(w_i)-f_w(x_j)\right\|^2_2\). Ideally we
want the same descriptors even if the two images have different backgrounds or different illuminations. - Implementation Aspects:
![]()
To assemble a mini-batch we start by randomly taking one training sample from each object. Additionally, for each of them we add its template with the most similar pose. Pairs are then formed by associating each training sample with its closest template. For each training sample in the mini-batch we initially create three triplets. For each training sample we add two additional triplets.



 浙公网安备 33010602011771号
浙公网安备 33010602011771号