6D姿态估计从0单排——看论文的小鸡篇——Hashmod: A Hashing Method for Scalable 3D Object Detection
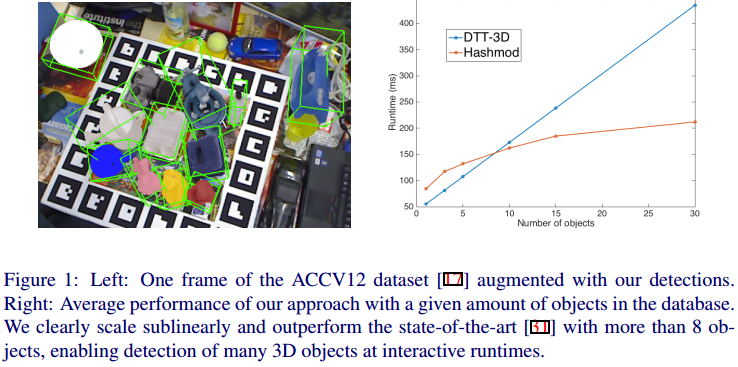
To this end, we rely on an efficient representation of object views and employ hashing techniques to match these views against the input frame in a scalable way.
Our approach to 3D object detection is based on 2D view-specific templates which cover the appearance of the objects over multiple viewpoints. Since viewpoints include the whole object, they can generally handle objects with poor visual features, however they have not been shown to scale well with the number of images so far. We apply hash functions to image descriptors computed over bounding boxes centered at each image location of the scene, so to match them efficiently against a large descriptor database of model views. In our work, we rely on the LineMOD descriptor.
Hashing for Object Recongnition and 3D Pose Estimation

\(M\) objects, \(N\)views for each object from poses regularly sampled on a hemisphere of a given radius. From this, we compute a set \(D\) of d-dimensional binary descriptors: \(D=\{x_{1,1},...,x_{M,N}\}\), where \(x_{i,j}\in B^d\) is the descriptor for the \(i\)-th object seen under the \(j\)-th pose. We use LineMOD in practice to compute these descriptors.
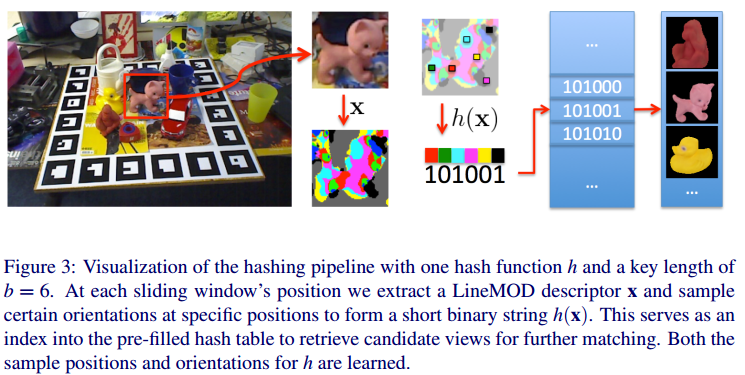
As usually done in template-based approaches, we parse the image with a sliding window looking for the objects of interest. We extract at each image location the corresponding descriptor \(x\). If the distance between \(x\) and its nearest neighbor \(x_{i,j}\) in \(D\) is small enough, it is very likely that the image location contains object \(i\) under pose \(j\). We tackle the issue of object scale and views of different 2D sizes by dividing the views up into clusters \(D_s \subset D\) of similar scale \(s\).
- Selecting the Hashing Keys
The descriptors \(x\) are already binary strings, we design our hashing functions \(h(x)\) to return a short binary string made of \(b\) bits directly extracted from \(x\).
Randomness-based selection: Given a set of descriptors, we select the b bits randomly among all possible d bits. Some bits are more discriminant than others in our template representation.
Probability-based selection: we focus on the bits for which the probabilities of being 0 and 1 are close to 0:5 with a given set of descriptors. This strategy provides a high accuracy since it focuses on the most discriminant bits. However, This strategy results in a high variance in the number of elements per bucket.
Tree-based selection: Starting with a set of descriptors at the root, we determine the bit that splits this set into two subsets with sizes as equal as possible, and use it as the first bit of the key. For the second bit, we decide for the one that splits those two subsets further into four equallysized subsets and so forth. We stop if b bits have been selected or one subset becomes empty. The \(j\)-th bit \(B\) of the key is selected bt solving: \({\arg\min}_B\sum_i\left||S^B_L(N_i)|-|S^B_R(N_i)|\right|\), where \(N_i \subset D\) is the set of descriptors contained by the \(i\)-th node at level \(j\).
![]()
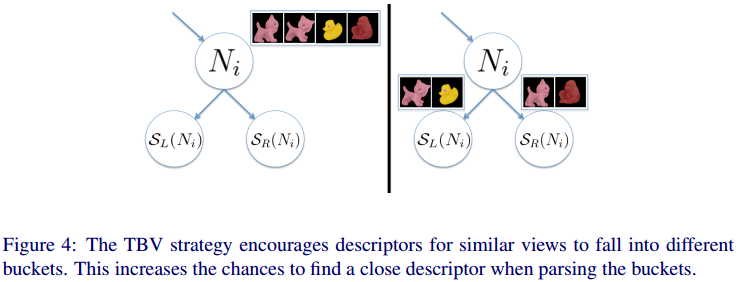
Tree-based selection with view scattering: To improve detection rates we favor similar views of the same object to go into different branches. The idea behind this strategy is to reduce misdetections due to noise or clutter in the descriptor. We optimize the previous criterion with an additional term: \({\arg\min}_B\frac{1}{N_i}\sum\left||S^B_L(N_i)|-|S^B_R(N_i)|\right|+\frac{1}{|N_i|^2}(P(S_L^B(N_i))+P(S_R^B(N_i)))\), where
![]()
, where \(\mathbb{I}(x,y)\) indicates if decriptors \(x\) and \(y\) encode views of the same object and \(q_x,q_y\) are the quaternions associated with the rotational part of the descriptor's poses. - Remarks on the Implementation
we disallowed all bits closer than T to
be selected for the same LineMOD value. This forces the bit selection to take different values and positions into account


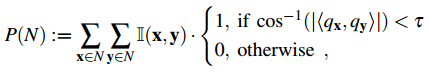

 浙公网安备 33010602011771号
浙公网安备 33010602011771号