算法62---最长回文子序列长度(子串)、回文子序列总共个数(子串)【动态规划】
参考链接:https://www.cnblogs.com/AndyJee/p/4465696.html
一、题目:最长回文子序列长度
给定字符串,求它的最长回文子序列长度。回文子序列反转字符顺序后仍然与原序列相同。例如字符串abcdfcba中,最长回文子序列长度为7,abcdcba或abcfcba。
思路:动态规划:时间O(N^2),空间O(N^2)
对于任意字符串,如果头尾字符相同,那么字符串的最长子序列等于去掉首尾的字符串的最长子序列加上首尾;如果首尾字符不同,则最长子序列等于去掉头的字符串的最长子序列和去掉尾的字符串的最长子序列的较大者。
例子:abba最长回文子序列个数为4,先判断首尾的'a'和‘a'是否相等,如果相等则’bb'最长个数+2=4,如果不等,则看'abb'和‘bba'谁的最长个数最大,值为哪个。
因此动态规划的状态转移方程为:
设字符串为str,长度为n,dp[i][j]表示第i到第j个字符间的子序列的个数(i<=j),则:
状态初始条件:dp[i][i]=1 (i=0:n-1)
状态转移方程:dp[i][j]=dp[i+1][j-1] + 2 if(str[i]==str[j])
dp[i][j]=max(dp[i+1][j],dp[i][j-1]) if (str[i]!=str[j])
个数代码:如果只计算上三角的值,循环从右下方开始
def longestPal(string): if not string : return 0 dp = [[0] * len(string) for i in range(len(string))]
for i in range(len(s)):
dp[i][i] = 1
for i in range(len(string)-2,-1,-1): for j in range(i+1,len(string)): if string[i] == string[j]: dp[i][j] = dp[i+1][j-1] + 2 else: dp[i][j] = max(dp[i+1][j],dp[i][j-1]) return dp[0][-1] string= 'abcdfcba' longestPal(string)
二、题目:回文子序列个数
给定字符串,求它的回文子序列个数。回文子序列反转字符顺序后仍然与原序列相同。例如字符串aba中,回文子序列为"a", "a", "aa", "b", "aba",共5个。内容相同位置不同的子序列算不同的子序列。
思路:动态规划:时间O(N*N),空间O(N*N)
对于任意字符串,如果头尾字符不相等,则字符串的回文子序列个数就等于去掉头的字符串的回文子序列个数+去掉尾的字符串的回文子序列个数-去掉头尾的字符串的回文子序列个数;如果头尾字符相等,那么除了上述的子序列个数之外,还要加上首尾相等时新增的子序列个数,1+去掉头尾的字符串的回文子序列个数,1指的是加上头尾组成的回文子序列,如aa,bb等。
因此动态规划的状态转移方程为:
设字符串为str,长度为n,p[i][j]表示第i到第j个字符间的最长子序列的长度(i<=j),则:
状态初始条件:dp[i][i]=1 (i=0:n-1)
状态转移方程:dp[i][j]=dp[i+1][j] + dp[i][j-1] - dp[i+1][j-1] if(str[i]!=str[j])
dp[i][j]=dp[i+1][j] + dp[i][j-1] - dp[i+1][j-1]+dp[i+1][j-1]+1=dp[i+1][j] + dp[i][j-1]+1 if (str[i]==str[j])
代码:
def palNum(string): if not string : return 0 dp = [[0] * len(string) for i in range(len(string))] for i in range(len(string)): dp[i][i] = 1 for i in range(len(string)-2,-1,-1): for j in range(i+1,len(string)): if string[i] != string[j]: dp[i][j] = dp[i][j-1] + dp[i+1][j] - dp[i+1][j-1] else: dp[i][j] = dp[i][j-1] + dp[i+1][j] + 1 return dp[0][-1] string= 'abba' palNum(string)
三、题目:最长回文子串
思路1:借助最长公共子串问题,将原来的string翻转,求两个字符串的最长公共子串。
思路2:动态规划:dp[i,j]=1表示str[i...j]是回文子串,必定存在dp[i+1,j-1]=1。【0
状态方程:
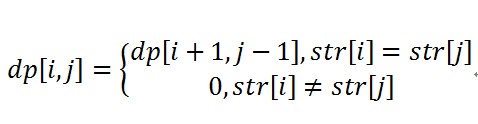
初始状态:dp = [[1] * len(n) for i in range(n)]
dp[i][i]=1
思路2代码:
def longestpalSub(string): if not string : return 0 maxres,temp = 0,0 dp = [[1] * len(string) for i in range(len(string))] for i in range(len(string)): dp[i][i] = 1 for i in range(len(string)-2,-1,-1): for j in range(i+1,len(string)): if string[i] != string[j]: dp[i][j] = 0 temp = 0 else: dp[i][j] = dp[i+1][j-1] if dp[i][j] == 1: temp = j-i+1 maxres = max(maxres,temp) return maxres string= 'cabbaci' longestpalSub(string)
四、题目:回文串个数
思路:动态规划:dp[i][j]表示子串str[i...j]是否是回文串。
该题创建的dp矩阵和题三是一样的,但是,题三是求dp[i][j] = 1时,j-i+1最大值,该题求的是dp上三角矩阵出现1的总个数。
初始状态:dp = [[1] * len(n) for i in range(n)]
dp[i][i]=1
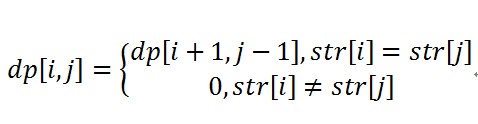
代码:
#动态规划 if not s: return 0 n = len(s) res = n dp = [[1] * n for i in range(n)]
for i in range(n-2,-1,-1): for j in range(i+1,n): if s[i] == s[j]: dp[i][j] = dp[i+1][j-1] if dp[i][j] == 1: res += 1 else: dp[i][j] = 0 return res
五、最长的斐波那契子序列的长度
如果序列 X_1, X_2, ..., X_n 满足下列条件,就说它是 斐波那契式 的:
n >= 3- 对于所有
i + 2 <= n,都有X_i + X_{i+1} = X_{i+2}
给定一个严格递增的正整数数组形成序列,找到 A 中最长的斐波那契式的子序列的长度。如果一个不存在,返回 0 。
(回想一下,子序列是从原序列 A 中派生出来的,它从 A 中删掉任意数量的元素(也可以不删),而不改变其余元素的顺序。例如, [3, 5, 8] 是 [3, 4, 5, 6, 7, 8] 的一个子序列)
示例 1:
输入: [1,2,3,4,5,6,7,8] 输出: 5 解释: 最长的斐波那契式子序列为:[1,2,3,5,8] 。
示例 2:
输入: [1,3,7,11,12,14,18] 输出: 3 解释: 最长的斐波那契式子序列有: [1,11,12],[3,11,14] 以及 [7,11,18] 。
提示:
3 <= A.length <= 10001 <= A[0] < A[1] < ... < A[A.length - 1] <= 10^9- (对于以 Java,C,C++,以及 C# 的提交,时间限制被减少了 50%)
思路:动态规划,时间O(n2),空间O(n2)
采用字典dic存储数组的索引。
dp[i][j]存的是从第i个到第j个最长斐波那契子序列的长度
temp = arr[i] + arr[j]
if temp in dic:
position = dic[temp]
dp[i][j] = dp[j][position] + 1
else:
dp[i][j] = 2
代码:
def lenLongestFibSubseq(A): """ :type A: List[int] :rtype: int """ if not A: return 0 dic = {} res = 0 for i in range(len(A)): dic[A[i]] = i dp = [[0] * len(A) for i in range(len(A))] for i in range(len(A)-2,-1,-1): for j in range(i+1,len(A)): temp = A[i] + A[j] if temp in dic: position = dic[temp] dp[i][j] = dp[j][position] + 1 res = max(res,dp[i][j]) else: dp[i][j] = 2 return res
六、题目:摆动序列
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为摆动序列。第一个差(如果存在的话)可能是正数或负数。少于两个元素的序列也是摆动序列。
例如, [1,7,4,9,2,5] 是一个摆动序列,因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
给定一个整数序列,返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些(也可以不删除)元素来获得子序列,剩下的元素保持其原始顺序。
示例 1:
输入: [1,7,4,9,2,5] 输出: 6 解释: 整个序列均为摆动序列。
示例 2:
输入: [1,17,5,10,13,15,10,5,16,8] 输出: 7 解释: 这个序列包含几个长度为 7 摆动序列,其中一个可为[1,17,10,13,10,16,8]。
示例 3:
输入: [1,2,3,4,5,6,7,8,9] 输出: 2
思路:时间O(n2),空间O(n2)
两个dp数组p和q,
p[i]表示到i位置时首差值为正的摆动子序列的最大长度,
q[i]表示到i位置时首差值为负的摆动子序列的最大长度。
我们从i=1开始遍历数组,然后对于每个遍历到的数字,再从开头位置遍历到这个数字,然后比较nums[i]和nums[j],分别更新对应的位置
p[i] = max(p[i],q[j]+1)【nums[i] > nums[j]】
q[i] = max(q[i],p[j] + 1) 【nums[i] < nums[j] 】
代码:
def wiggleMaxLength(nums): """ :type nums: List[int] :rtype: int """ if not nums: return 0 p = [1] * len(nums) q = [1] * len(nums) for i in range(1,len(nums)): for j in range(0,i): if nums[i] > nums[j]: p[i] = max(p[i],q[j] + 1) elif nums[i] < nums[j]: q[i] = max(q[i],p[j] + 1) return max(q[-1],p[-1])

