算法60---石子游戏/传球游戏【动态规划】

一、题目：

亚历克斯和李用几堆石子在做游戏。偶数堆石子排成一行，每堆都有正整数颗石子 piles[i] 。

游戏以谁手中的石子最多来决出胜负。石子的总数是奇数，所以没有平局。

亚历克斯和李轮流进行，亚历克斯先开始。 每回合，玩家从行的开始或结束处取走整堆石头。 这种情况一直持续到没有更多的石子堆为止，此时手中石子最多的玩家获胜。

假设亚历克斯和李都发挥出最佳水平，当亚历克斯赢得比赛时返回 true ，当李赢得比赛时返回 false 。

 

示例：

输入：[5,3,4,5]
输出：true
解释：
亚历克斯先开始，只能拿前 5 颗或后 5 颗石子 。
假设他取了前 5 颗，这一行就变成了 [3,4,5] 。
如果李拿走前 3 颗，那么剩下的是 [4,5]，亚历克斯拿走后 5 颗赢得 10 分。
如果李拿走后 5 颗，那么剩下的是 [3,4]，亚历克斯拿走后 4 颗赢得 9 分。
这表明，取前 5 颗石子对亚历克斯来说是一个胜利的举动，所以我们返回 true 。

 

提示：

1. 2 <= piles.length <= 500
2. piles.length 是偶数。
3. 1 <= piles[i] <= 500
4. sum(piles) 是奇数。

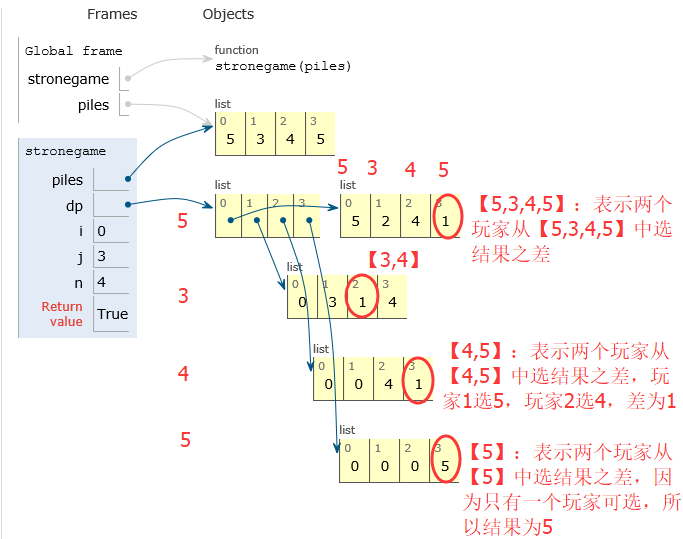
思路：动态规划：时间O（N^2），空间O（N^2）

• dp[i][j]表示：表示在piles中下标 i 至下标 j 之间的玩家1 所拿石子总数和 玩家2所拿石子总数之差。dp[i][j] > 0 表明玩家1赢，输出True
• 子问题：dp[ i+1 ][ j ]和dp[ i ][ j-1 ]
• 初始状态：dp的初始状态是 i = j 即只有一个石子堆，由于玩家1先拿，则 dp[ i ][ j ] = piles[ i ]
• 状态方程：

dp[ i ][ j ] = max( piles[ i ] - dp[ i+1 ][ j ], piles[ j ] - dp[ i ][ j-1 ])

【解释：当玩家1拿了最左边下标为 i 的石子后，玩家1和玩家2的石子数之差为 piles[ i ] - dp[ i+1 ][ j ], 当玩家1拿了最右边下标为j的那堆石子后，玩家1和玩家2的石子数之差为 piles[ j ] - dp[ i ][ j-1 ], 取其中较大者为新的最优解。】

 

代码：

def stronegame(piles):
    n = len(piles)
    dp = [[0] * n for i in range(n)]
    for i in range(n):
        dp[i][i] = piles[i]
    for i in range(n-2,-1,-1):
        for j in range(i+1,n):
            dp[i][j] = max(piles[i]-dp[i+1][j],piles[j]-dp[i][j-1])
    return dp[0][-1] > 0
piles = [5,3,4,5]
stronegame(piles)

 二、题目：传球游戏

k个猿辅导老师，传一个球，传n次，球从A老师手里开始传，又传回A老师手里的传球方式有多少种？(每次可以传给除自己外的任何一个人)比如输入k=3，n=3，那么输出为2。只有二种传球方式:abca,acba

这个题，递推即可，每一个传球，只有两种可能，一种球在A老师手里，一种球不在A老师手里
令dp[n][0]表示球在A老师手里的方案数，令dp[n][1]表示球不在A老师手里的方案数，于是
dp[n+1][0]=dp[n][1]
dp[n+1][1]=dp[n][0]*k+dp[n][1]*(k-1)