算法57----字符串匹配问题【动态规划】
一、题目:交错字符串
给定三个字符串 s1, s2, s3, 验证 s3 是否是由 s1 和 s2 交错组成的。
示例 1:
输入: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac" 输出: true
示例 2:
输入: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc" 输出: false
思路:动态规划:时间O(M*N ),空间O(M*N)
构造一个(M+1)*(N+1)的矩阵dp:dp[i][j] 代表是s1的前i个字符与s3中匹配,s2中前j个字符与s3中匹配.
- 初始化:首行首列则是假设其中一个字符串为空时,另一个字符串是否与目标字符串一一对应。
- dp[0][0]=true. # s3为空时可以由str1和str2的空字符串组成
- dp[i][0]:表示s3[0...i-1]能否由str1[0.....i-1]组成,若可以则dp[i][0]=true,反之则为false
- dp[i][0] = dp[i-1][0] and s1[i-1][0] == s3[i-1][0]
- dp[0][j]:表示s3[0...j-1]能否由str2[0.....j-1]组成,若可以则dp[0][j]=true,反之则为false
- dp[0][j] = dp[0][j-1] and s2[j-1] == s3[j-1]
- 状态方程:其他位置(i,j),dp[i][j]的值:
dp[i][j] = (dp[i-1][j] == True and s1[i-1] == s3[i+j-1]) or (dp[i][j-1] ==True and s2[j-1] == s3[i+j-1])
- dp[i-1][j]:代表s3[i+j-2]能否被str1[0...i-2]和str2[0...j-1]交错组成,若可以,以及str1[i-1]等于s3[i+j-1],则dp[i][j]=true,反之则为false
- dp[i][j-1]:代表s3[i+j-2]能否被str1[0...i-1]和str2[0...j-2]交错组成,若可以,以及str2[j-1]等于s3[i+j-1],则dp[i][j]=true,反之则为false
- 若前两种情况都不满足,则dp[i][j]=false

代码:
def isInterleave(s1, s2, s3): if len(s3) != len(s2) + len(s1): return False dp = [[False] * (len(s2)+1) for i in range(len(s1)+1)]
#初始化 dp[0][0] = True for j in range(1,len(s2)+1): dp[0][j] = dp[0][j-1] and s2[j-1] == s3[j-1] for i in range(1,len(s1)+1): dp[i][0] = dp[i-1][0] and s1[i-1][0] == s3[i-1][0]
#状态方程 for i in range(1,len(s1)): for j in range(1,len(s2)): dp[i][j] = (dp[i-1][j] == True and s1[i-1] == s3[i+j-1]) or (dp[i][j-1] ==True and s2[j-1] == s3[i+j-1]) return dp[-1][-1] s1 = "aabcc" s2 = "dbbca" s3 = "aadbbcbcac" isInterleave(s1, s2, s3)
二、题目:正则化表达式匹配【含通配符】
给定一个正则字符串p,一个字符串s。要求验证s和p是否能匹配。
特别的,正则字符串中仅由两个特殊字符:'.'表示任意的单个字符,'*'表示其前方紧邻元素连续出现0个或者更多个。要求匹配需要覆盖整个输入字符串,而不是部分的匹配。
s 可能为空,且只包含从 a-z 的小写字母。
p 可能为空,且只包含从 a-z 的小写字母,以及字符 . 和 *。
思路:动态规划:
状态转移数组 f [i] [j] 表示利用 p 的前 i 个字符匹配 s 的前 j 个字符的匹配结果(成功为true,失败为false)。
边界:
- dp[0][0] = True,s和p都是空格。
- i = 0,只有p为这种情况 p = ‘a*b*c*'才能True,别的都为False。
for i in range(1,len(p)+1):
if p[i-1] == '*': if i >= 2:
dp[0][i] = dp[0][i-2]
- j = 0,全部为False。即p为空,都False。
非边界:
如果s[i] == p[j] 或者 p[j] == '.':【如果s的最后一位和p的最后一位相同,则只需要判断前面的】
dp[i][j] = dp[i - 1][j - 1]
如果p[j] == '*':【dp[i][j-2]:*前面一位为0个即可,Sx~P】【dp[i][j-1]:*前面一位为1个,Sx~Pz】【dp[i-1][j]:*匹配x(x==z或者z=='.'), S~Pzy】
dp[i][j] = dp[i][j-2] || dp[i][j-1] || (dp[i-1][j] and (s[i-1]==p[j-2] or p[j-2]=='.'))
解释:
对于s和p,设各个最后一个字符为x, y,p的倒数第二字符为z,除此外前面字符设为S,P,则:
s = Sx
p = Pzy
- 如果x == y或y == '.',则如果S和Pz匹配,则s和p匹配,因为最后两字字母是匹配的。这就缩减了问题规模。
- 而对于y == '*'的情况,需要考虑z:
如果x != z,则只有在s和P匹配的情况下,s和p才匹配。
如果x == z,设匹配符号为~吧,方便,则如果S~Pzy,Sx~P,Sx~Pz,【S~P,S~Pz也匹配】都可得出s和p匹配。
代码:
def isMatch(self, s, p): """ :type s: str :type p: str :rtype: bool """ dp = [[False] * (len(p) + 1) for i in range(len(s) + 1)] dp[0][0] = True for i in range(1,len(p)+1): if p[i-1] == '*': if i >= 2: dp[0][i] = dp[0][i-2] for i in range(1,len(s)+1): for j in range(1,len(p)+1): if p[j-1]=='.' or s[i-1] == p[j-1]: dp[i][j] = dp[i-1][j-1] elif p[j-1]=='*': dp[i][j] = dp[i][j-2] or dp[i][j-1] or (dp[i-1][j] and (s[i-1]==p[j-2] or p[j-2]=='.')) return dp[len(s)][len(p)]
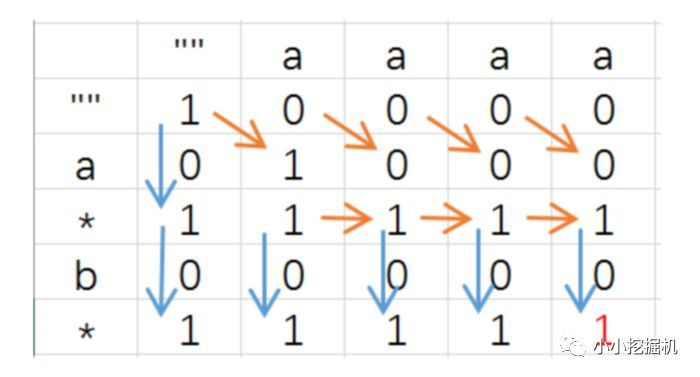
三、题目:字符串匹配【含通配符?*】
请你写个程序判断对于给定字符串s,字符串p是否能与其匹配。s串仅包含字母,p串可以包含字母和字符'?'、'*'。匹配的规则如下:
'?'可以匹配任意一位英文字母(不区分大小写)
'*'用于表示任意多位英文字母(不区分大小写,可以是0位)
例如,字符串“ab*ba*a*”和“a?b*abbbb”都可匹配字符串“abbababbbb”。
思路:动态规划:时间O(M*N),空间O(M*N)
bp[i][j]表示s的前i个字符和p的前j个字符是否匹配。
边界:
- bp[0][0] = True
- b[0][j]的值取决于p前一个位置是否为‘*’以及前一情况是否匹配。
非边界:
- 当p[j]等于‘?’或者s[i] == p[j]时,则 bp[i][j] 的值取决于 bp[i-1][j-1],即为s的前一位置和p的前一位置是否匹配;
- 当p[j]等于‘*’时,如果该‘*’可以匹配s中的0个或者1个字符,分别对应bp[i][j-1],即s的当前位置和p的前一位置是否匹配,以及bp[i-1][j-1],即s的前一位置和p的前一位置是否匹配。
代码:
def isMatch(s, p): dp = [[False] * (len(p) + 1) for i in range(len(s) + 1)] #边界 dp[0][0] = True for j in range(1,len(p)+1): #边界 dp[0][j] = dp[0][j-1] and p[j-1] == '*' for i in range(1,len(s)+1): if p[j-1] == '?' or s[i-1] == p[j-1]: dp[i][j] = dp[i-1][j-1] elif p[j-1] == '*': dp[i][j] = bp[i][j-1] or dp[i-1][j-1] return dp[len(s)][len(p)] s = 'a' p = 'a***b*a' isMatch(s, p)
四、题目:leetcode[115] Distinct Subsequences
给定字符串S和T,S通过删除某些位置的字符得到T的话,就记作一种subSequence。返回总共有几种。
Here is an example:
S = "rabbbit", T = "rabbit"
思路:动态规划

dp[i][j]表示T的从0开始长度为i的子串和S的从0开始长度为j的子串的匹配的个数。那么最后目标就是dp[len(S)][len(T)];
比如, dp[2][3]表示T中的ra和S中的rab的匹配情况。
边界:
dp[0][0] = 1; // T和S都是空串.
dp[0][ 1 ... len(S) ] = 1; // T是空串,S只有一种子序列匹配。
dp[1 ... len(T) ][0] = 0; // S是空串,T不是空串,S没有子序列匹配。
非边界:
- 显然,至少有dp[i][j] = dp[i][j - 1].
比如, 因为T 中的"ra" 匹配S中的 "ra", 所以dp[2][2] = 1 。 显然T 中的"ra" 也匹配S中的 "rab",所以s[2][3] 至少可以等于dp[2][2]。
- 如果T[i-1] == S[j-1], 那么dp[i][j] = dp[i][j - 1] + (T[i - 1] == S[j - 1] ? dp[i - 1][j - 1] : 0);
比如, T中的"rab"和S中的"rab"显然匹配,
根据(1), T中的"rab"显然匹配S中的“rabb”,所以dp[3][4] = dp[3][3] = 1,
根据(2), T中的"rab"中的b等于S中的"rab1b2"中的b2, 所以要把T中的"rab"和S中的"rab1"的匹配个数累加到当前的dp[3][4]中。 所以dp[3][4] += dp[2][3] = 2;
代码:
class Solution { public: int numDistinct(string S, string T) { vector<vector<int> > dp(T.length() + 1, vector<int>(S.length() + 1, 0)); dp[0][0] = 1; for (int i = 1; i < S.length() + 1; ++i) dp[0][i] = 1; for (int i = 1; i < T.length() + 1; ++i) dp[i][0] = 0; for (int i = 1; i < T.length() + 1; ++i) { for (int j = 1; j < S.length() + 1; ++j) { dp[i][j] = dp[i][j - 1]; if (S[j - 1] == T[i - 1]) dp[i][j] += dp[i - 1][j - 1]; } } return dp[T.length()][S.length()]; } };
五、题目:字符串匹配
有一个字符串"BBC ABCDAB ABCDABCDABDE",里面是否包含另一个字符串"ABCDABD"?如果匹配则返回True,否则FALSE。
