算法56-----最小编辑代价【动态规划】

一、题目：最小编辑代价

给定两个字符串str1和str2，再给定三个整数ic，dc，rc，分别代表插入、删除、替换一个字符的代价，返回将str1编辑成str2的最小代价。
举例：
str1="abc"   str2="adc"  ic=5    dc=3   rc=2，从"abc"编辑到"adc"把b替换成d代价最小，为2；
str1="abc"   str2="adc"  ic=5    dc=3   rc=10，从"abc"编辑到"adc"，先删除b再插入d代价最小，为8；

思路：动态规划：时间O（M*N），空间O（M*N)

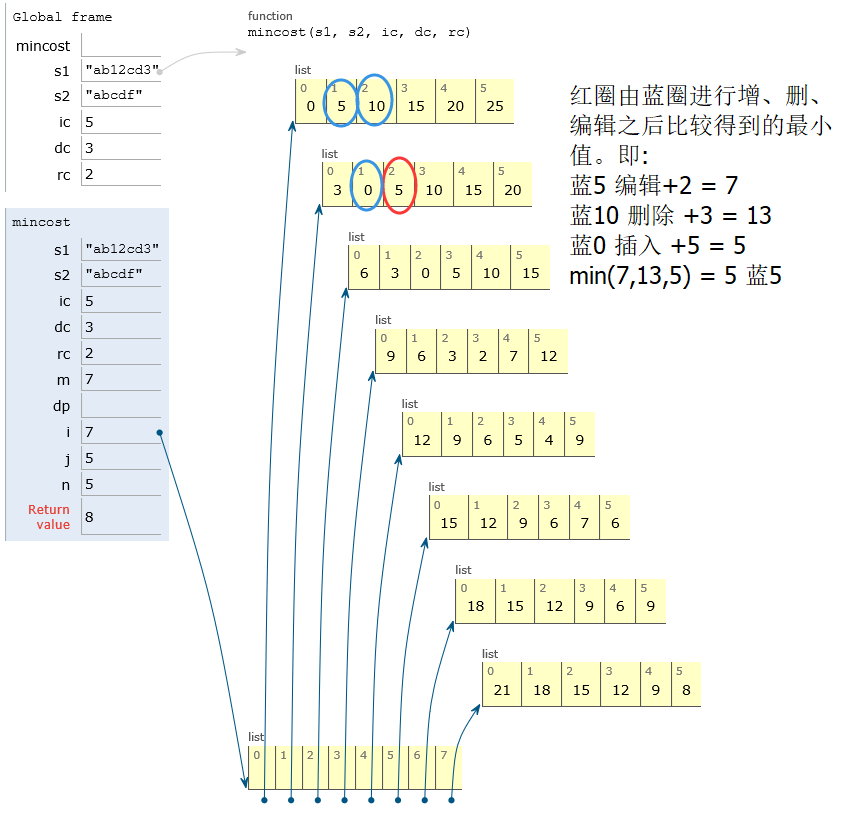
动态规划表：dp[i][j]表示str1[0......i-1]编辑成str2[0......j-1]的最小编辑代价，dp大小为(M+1)*(N+1)是为了从空串开始计算，即dp[0][0]表示空串编辑到空串的最小编辑代价。

状态方程：

• 初始化：

dp[0][0] = 0

dp[0][j] = j * len(s2)

dp[i][0] = i * len(s1)

• dp[i][j] = min( dp[i][j-1]+ic , dc+dp[i-1][j] , dp[i-1][j-1] + rc 【如果str1[i-1]==str2[j-1]，rc = rc，否则，rc = 0】）

1.dp[0][0]表示空串编辑成空串，故dp[0][0]=0;
2.求第一行dp[0][j]，空串编辑成str2[0....j-1]，则dp[0][j]=ic*j;
3.求第一列dp[i][0]，str1[0......i-1]编辑成空串，则dp[i][0]=dc*i;
4.求dp[i][j]，即str1[0....i-1]编辑成str2[0.....j-1]，三种可能的途径：
<1>str1[0....i-1]先编辑成str2[0.....j-2]，再由str2[0.....j-2]插入到str2[0.....j-1]，即 dp[i][j-1] + ic;
<2>str1[0....i-1]先编辑成str1[0.....i-2]，再由str1[0.....i-2]删除到str2[0.....j-1]，即 dp[i-1][j] + dc;
<3>如果str1[i-1]==str2[j-1],则 dp[i][j] = dp[i-1][j-1];
       如果str1[i-1]!=str2[j-1],则 dp[i][j] = dp[i-1][j-1] + rc;

最后比较三种途径的最小值，即dp[i][j]的值。

 

代码：

def mincost(s1,s2,ic,dc,rc):
    m , n = len(s1) , len(s2)
    if not s1:
        return n*ic
    if not s2:
        return m*dc
    dp = [[0] * (n+1) for i in range(m+1)]
    for i in range(1,n + 1):
        dp[0][i] = ic * i
    for j in range(1,m + 1):
        dp[j][0] = dc * j
    for i in range(1,m+1):
        for j in range(1,n+1):
            if s1[i-1] == s2[j-1]:
                dp[i][j] = dp[i-1][j-1]
            else:
                dp[i][j] = dp[i-1][j-1] + rc
            dp[i][j] = min( dp[i][j] , dp[i-1][j] + dc , dp[i][j-1] + ic)
    return dp[-1][-1]
s1 = 'ab12cd3'
s2 = 'abcdf'
ic , dc , rc = 5,3,2
mincost(s1,s2,ic,dc,rc)