算法55----最长子序列【动态规划】
一、题目:最长公共子序列:
给定两个字符串,求解这两个字符串的最长公共子序列(Longest Common Sequence)。比如字符串L:BDCABA;字符串S:ABCBDAB
则这两个字符串的最长公共子序列长度为4,最长公共子序列是:BCBA
思路:动态规划:时间O(n * m),空间O(n * m)
创建 DP数组C[i][j]:表示子字符串L【:i】和子字符串S【:j】的最长公共子序列个数。
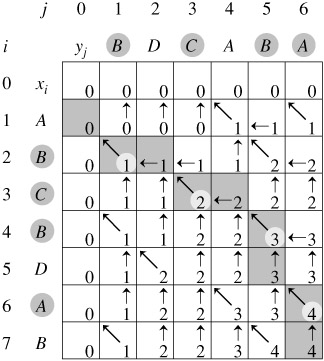
状态方程: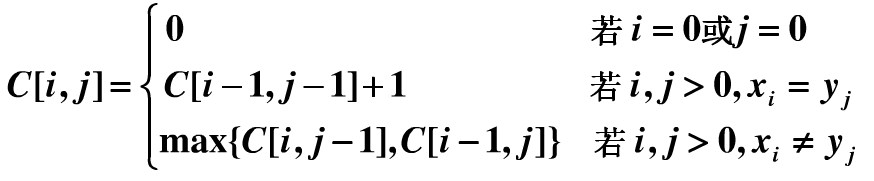
个数代码:
def LCS(L,S): if not L or not S: return "" dp = [[0] * (len(L)+1) for i in range(len(S)+1)] for i in range(len(S)+1): for j in range(len(L)+1): if i == 0 or j == 0: dp[i][j] = 0 else: if L[j-1] == S[i-1]: dp[i][j] = dp[i-1][j-1] + 1 else: dp[i][j] = max(dp[i-1][j],dp[i][j-1]) return dp[-1][-1] L = 'BDCABA' S = 'ABCBDAB' LCS(L,S)
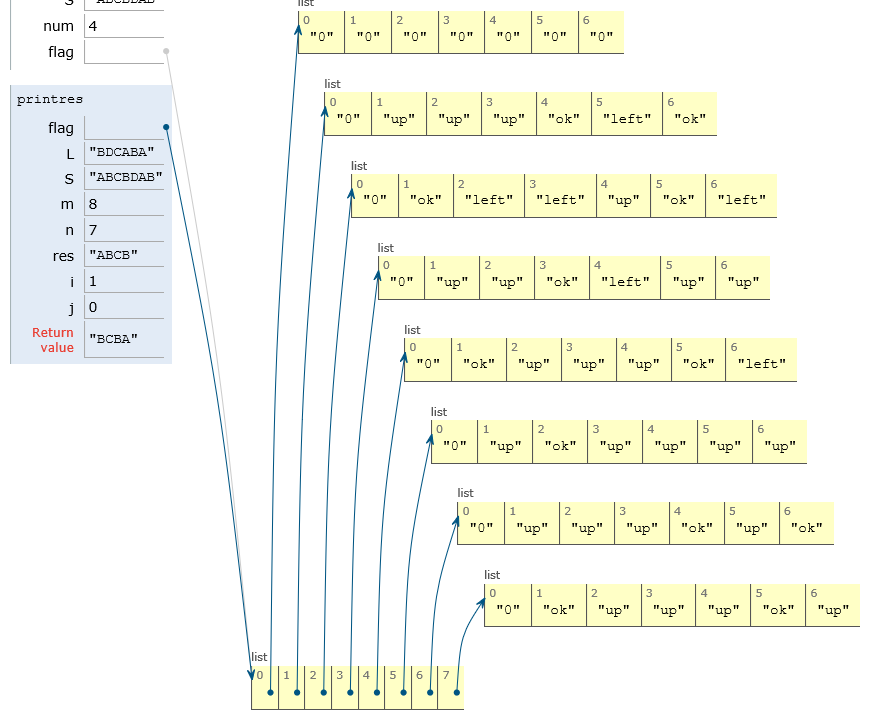
最长子序列代码:设置一个标志
def LCS(L,S): if not L or not S: return "" res = '' dp = [[0] * (len(L)+1) for i in range(len(S)+1)] flag = [['left'] * (len(L)+1) for i in range(len(S)+1)] for i in range(len(S)+1): for j in range(len(L)+1): if i == 0 or j == 0: dp[i][j] = 0 flag [i][j] = '0' else: if L[j-1] == S[i-1]: dp[i][j] = dp[i-1][j-1] + 1 flag[i][j] = 'ok' else: dp[i][j] = max(dp[i-1][j],dp[i][j-1]) flag[i][j] = 'up' if dp[i][j] == dp[i-1][j] else 'left' return dp[-1][-1],flag def printres(flag,L,S): m = len(flag) n = len(flag[0]) res = '' i , j = m-1 , n-1 while i > 0 and j > 0: if flag[i][j] == 'ok': res += L[j-1] i -= 1 j -= 1 elif flag[i][j] == 'left': j -= 1 elif flag[i][j] == 'up': i -= 1 return res[::-1] L = 'BDCABA' S = 'ABCBDAB' num,flag = LCS(L,S) res = printres(flag,L,S)
二、题目:最长递增子序列
给定一个长度为N的数组,找出一个最长的单调自增子序列(不一定连续,但是顺序不能乱)。例如:给定一个长度为6的数组A{5, 6, 7, 1, 2, 8},则其最长的单调递增子序列为{5,6,7,8},长度为4.
解法一:最长公共子序列:O(N^2)
这个问题可以转换为最长公共子序列问题。如例子中的数组A{5,6, 7, 1, 2, 8},则我们排序该数组得到数组A‘{1, 2, 5, 6, 7, 8},然后找出数组A和A’的最长公共子序列即可。显然这里最长公共子序列为{5, 6, 7, 8},也就是原数组A最长递增子序列。
解法二:动态规划法(时间复杂度O(N^2))
设 dp(j) 表示L中以 L[j] 为末元素的最长递增子序列的长度。状态方程:
dp(j) = { max(dp(i)) + 1, i<j且L[i]<L[j] }
这个递推方程的意思是,在求以L【j】为末元素的最长递增子序列时,找到所有序号在 j 前面且小于L【j】的元素L【i】,即 i < j 且 L【j】< L【i】。
例如给定的数组为{5,6,7,1,2,8},则 dp(0)=1, dp(1)=2, dp(2)=3, dp(3)=1, dp(4)=2, dp(5)=4。所以该数组最长递增子序列长度为4,序列为{5,6,7,8}。
代码:
def LCS1(L): if not L: return "" dp = [1] * len(L) for j in range(len(L)): for i in range(j):
#当j = 5,i = 0时,dp = [1,2,3,1,2,1]
#当j = 5,i = 0时,dp[5] = 1 < dp[0]+1,故dp(5)更新为dp[0]+1=2,
#当j = 5,i = 1时,dp[5] = 2 < dp[1]+1 =3,故dp(5)更新为dp[1]+1=3
#当j = 5,i = 2时,dp[5] = 4
#当j = 5,i = 3时,dp[5] = 4 > dp[3]+1 = 3,故dp[5]不更新,同理,i = 4时,dp[5]仍等于4 if L[j] > L[i] and dp[j] < dp[i] + 1:
dp[j] = dp[i]+1 return max(dp) L = [5,6,7,1,2,8] LCS1(L)
![]()
得到dp数组之后找出,最长递增子序列,
- 先找到dp最大值5,索引为7,然后arr【7】= 9
- dp【6】 = 5-1 =4,故arr【6】=8
- dp【4】 = 4-1或者dp【5】 = 4-1,故arr【4】 = 6 / arr【5】=4
- dp 【2】=3-1或者dp【3】 = 3-1,故arr【2】 = 5 / arr【3】=3
- 2 / 1
故最长递增子序列:2→5→6→8→9或者1→3→4→8→9
解法三:优化的动态规划,时间O(NlogN),空间效率最坏情况也是O(n),
5 9 4 1 3 7 6 7 2
那么:dp为以下情况,
5 //加入
5 9 //加入
4 9 //用4代替了5
1 9 //用1代替4
1 3 //用3代替9
1 3 7 //加入
1 3 6 //用6代替7
1 3 6 7 //加入
1 2 6 7 //用2代替3
该dp=【1,2,6,7】数组理解为到目前为止长度为1的递增子序列末尾最小为1,长度为2的递增子序列末尾最小为2,长度为3的递增子序列末尾最小为6,长度为4的递增子序列末尾最小为7.
而2代替3是找到比刚好2大的数3,这个查找过程通过二分查找,故时间复杂度为二分查找的O(NlogN)
最后b中元素的个数就是最长递增子序列的大小,即4。
要注意的是最后数组里的元素并不就一定是所求的序列,
例如如果输入 2 5 1
那么最后得到的数组应该是 1 5
而实际上要求的序列是 2 5
进阶题目:二维数组的最长递增子序列(生日礼物(京东2016实习生真题))
把卡片套装在一系列的信封A = {a1, a2, ..., an}中。小东已经从商店中购买了很多的信封,她希望能够用手头中尽可能多的信封包装卡片。为防止卡片或信封被损坏,只有长宽较小的信封能够装入大些的信封,同尺寸的信封不能套装,卡片和信封都不能折叠。

解题思路:
我们首先定义一个结构体,存放信封的长,宽,及其索引位置,然后把不能装卡片的信封去除掉(长宽较小的), 然后根据长或宽进行一个排序,这样就可以转化成一个最长递增子序列问题来求解了,2层循环动态规划就很容易求解了。
三、题目:最长递增子序列个数
给定一个未排序的整数数组,找到最长递增子序列的个数。
示例 1:
输入: [1,3,5,4,7] 输出: 2 解释: 有两个最长递增子序列,分别是 [1, 3, 4, 7] 和[1, 3, 5, 7]。
示例 2:
输入: [2,2,2,2,2] 输出: 5 解释: 最长递增子序列的长度是1,并且存在5个子序列的长度为1,因此输出5。
注意: 给定的数组长度不超过 2000 并且结果一定是32位有符号整数。
思路:动态规划,时间O(n2),空间O(n2)
定义 dp(n,1) count (n,1)
用dp[i]表示以nums[i]为结尾的递推序列的长度,
用cnt[i]表示以nums[i]为结尾的递推序列的个数,
初始化都赋值为1,只要有数字,那么至少都是1。
状态方程:
if nums[i] > nums[j] and dp[i] == dp[j] :
dp[i] = dp[j]+1
count[i] = count[j]
elif nums[i] > nums[j] and dp[i] == dp[j]+1:
count[i] += count[j]
代码:
def findNumberOfLIS(nums): # dp solution, 2 arrays # dp[i] stores the longest length ending at nums[i] # count[i] counts the number of paths with length dp[i] if not nums: return 0 n = len(nums) dp = [1] * n count = [1] * n for i in range(1, n): for j in range(i): if nums[i] > nums[j]: # dp[i] = max(dp[j]+1, dp[i]) # but we need to compute count also if dp[i] == dp[j]: dp[i] = dp[j]+1 count[i] = count[j] elif dp[i] == dp[j]+1: count[i] += count[j] maxLength = max(dp) return sum([count[i] for i in range(n) if dp[i] == maxLength]) nums = [1,3,5,4,6] findNumberOfLIS(nums)
四、题目:最大连续子序列(子串)
最大子序列是要找出由数组成的一维数组中和最大的连续子序列。比如{5,-3,4,2}的最大子序列就是 {5,-3,4,2},它的和是8,达到最大;而 {5,-6,4,2}的最大子序列是{4,2},它的和是6。你已经看出来了,找最大子序列的方法很简单,只要前i项的和还没有小于0那么子序列就一直向后扩展,否则丢弃之前的子序列开始新的子序列,同时我们要记下各个子序列的和,最后找到和最大的子序列。
import copy def maxSubSum(arr): if not arr: return 0 maxSum,curSum = 0,0 SubList,curlist = [],[] for i in range(len(arr)): if curSum + arr[i] > 0: curSum += arr[i] maxSum = curSum curlist.append(arr[i]) SubList = copy.deepcopy(curlist) else: curSum = 0 curlist = [] return maxSum,SubList arr = [5,-6,4,2,-1,3,-9] maxSubSum(arr)
五、题目:最长公共子串
找出两个字符串最长连续的公共字符串,如两个母串cnblogs和belong,最长公共子串为lo
思路:动态规划:时间O(N*M),空间O(N*M)
将二维数组c[i][j]用来记录具有这样特点的子串——结尾同时也为子串x1x2⋯xi与y1y2⋯yj的结尾的长度。
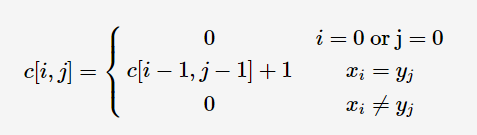
代码:
def lcs(s1,s2): if not s1 or not s2: return 0 c = [[0] * len(s2) for i in range(len(s1))] result = 0 for i in range(len(s1)): for j in range(len(s2)): if i == 0 or j == 0: c[i][j] = 0 else: if s1[i-1] == s2[j-1]: c[i][j] = c[i-1][j-1] + 1 result = max(c[i][j],result) else: c[i][j] = 0 return result s1 = 'cnblogs' s2 ='belong' lcs(s1,s2)
六、题目:最长公共子序列(3个字符串)
设A、B、C是三个长为n的字符串,它们取自同一常数大小的字母表。设计一个找出三个串的最长公共子序列的O(n^3)的时间算法。
思路:跟上面的求2个字符串的公共子序列是一样的思路,只不过这里需要动态申请一个三维的数组,三个字符串的尾字符不同的时候,考虑的情况多一些而已。
七、题目:判断s是否为t的子序列:
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
你可以认为 s 和 t 中仅包含英文小写字母。字符串 t 可能会很长(长度 ~= 500,000),而 s 是个短字符串(长度 <=100)。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。
示例 1:
s = "abc", t = "ahbgdc"
返回 true.
示例 2:
s = "axc", t = "ahbgdc"
返回 false.
后续挑战 :
如果有大量输入的 S,称作S1, S2, ... , Sk 其中 k >= 10亿,你需要依次检查它们是否为 T 的子序列。在这种情况下,你会怎样改变代码?
思路:动态规划:dp[i]表示:s[i] 是否在t中,在则True,不在则False。
初始化:dp = [False] * len(s)
状态方程:if s[i] == t[j],则dp[i] = True, i+=1,j += 1,否则,j+=1【继续找,直到找到t的尾部】
代码:
def isSubsequence(self, s, t): """ :type s: str :type t: str :rtype: bool """ if not s: return True if not t or len(s) > len(t): return False i , j = 0 , 0 dp = [False] * len(s) while i < len(s) and j < len(t): if s[i] == t[j]: dp[i] = True i += 1 j += 1 else: j += 1 return all(dp)
八、题目:平方串
如果一个字符串S是由两个字符串T连接而成,即S = T + T, 我们就称S叫做平方串,例如"","aabaab","xxxx"都是平方串.
牛牛现在有一个字符串s,请你帮助牛牛从s中移除尽量少的字符,让剩下的字符串是一个平方串。换句话说,就是找出s的最长子序列并且这个子序列构成一个平方串。
思路:动态规划:时间O(n^3),空间O(n^2)
首先将字符串s分为s1和s2,求s1和s2最长公共子序列。
拆分s1和s2有n种,如s = ‘ frankfurt',一、s1 = 'f',s2='rankfurt'。二、s1 ='fr',s2 = ’ankfurt‘……
故该方法时间复杂度为n3
代码:
def test(): s = input() res = 0 for i in range(len(s)-1): res = max(res,lcs(s,i)) return 2*res def lcs(s,i): s1 = s[:i+1] s2 = s[i+1:] dp = [[0] * (len(s2)+1) for i in range(len(s1)+1)] for i in range(1,len(s1)+1): for j in range(1,len(s2)+1): if s1[i-1] == s2[j-1]: dp[i][j] = dp[i-1][j-1] + 1 else: dp[i][j] = max(dp[i-1][j],dp[i][j-1]) return dp[-1][-1] if __name__ == '__main__': print(test())
九、题目:乘积最大子序列
给定一个整数数组 nums ,找出一个序列中乘积最大的连续子序列(该序列至少包含一个数)。
示例 1:
输入: [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
示例 2:
输入: [-2,0,-1] 输出: 0 解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
思路:设置两个变量,一个存储当前最大值,一个存储最小值。
访问到每个点的时候,以该点为子序列的末尾的乘积,要么是该点本身,要么是该点乘以以前一点为末尾的序列,注意乘积负负得正,故需要记录前面的最大最小值。
代码:
def test(nums): if not nums: return 0 minnum = nums[0] maxnum = nums[0] res = nums[0] for i in range(1,len(nums)): minnum = min([nums[i],minnum*nums[i],maxnum*nums[i]]) maxnum = max([nums[i],maxnum*nums[i],minnum*nums[i]]) res = max(res,maxnum) return res nums = [2,3,-2,4] test(nums)

