栈和队列(3)----算法
一、题目:生成窗口最大值数组(要求时间复杂度为O(N))
有一个整型数组arr和一个大小为w的窗口从数组的最左边滑到最右边,窗口每次向右边滑一个位置。


思路:
来自 https://blog.csdn.net/qq_32583189/article/details/53055618?utm_source=copy
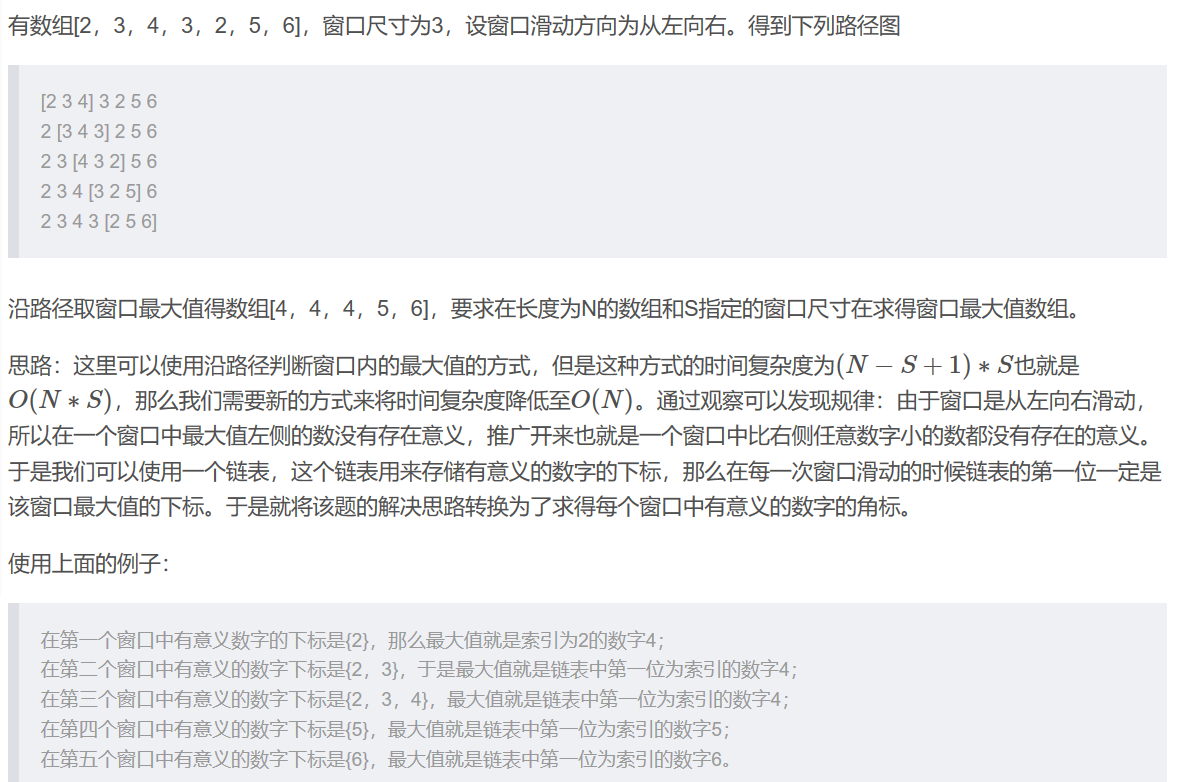
滑动窗口的最大值总是保存在队列首部,队列里面的数据总是从大到小排列。
当遇到比当前滑动窗口最大值更大的值时,则将队列清空,并将新的最大值插入到队列中。
如果遇到的值比当前最大值小,则直接插入到队列尾部。
每次移动的时候需要判断当前的最大值是否在有效范围,如果不在,则需要将其从队列中删除。
由于每个元素最多进队和出队各一次,因此该算法时间复杂度为O(N)。
代码:

def getMaxWindow(arr, w): if arr == None or w < 1 or len(arr) < w: return None deque = [] res = [] for i in range(len(arr)): #若队列不为空 且 队尾 比 当前元素小,则将队尾数据删除 while deque and arr[deque[-1]] <= arr[i]: deque.pop() #否则【队列为空】或者 【当前元素比队尾元素小】,将当前元素加入队列中 deque.append(i) #如果队首元素不在滑动窗口范围内,则删除队首元素。 if deque[0] <= i - w: deque.pop(0) #将结果加入res中 if i-w+1 >= 0: res.append(arr[deque[0]]) return res arr = [4,3,5,4,3,3,6,7] w = 3 getMaxWindow(arr, w)
二、题目:503. 下一个更大元素 II
给定一个循环数组(最后一个元素的下一个元素是数组的第一个元素),输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 -1。
示例 1:
输入: [1,2,1] 输出: [2,-1,2] 解释: 第一个 1 的下一个更大的数是 2; 数字 2 找不到下一个更大的数; 第二个 1 的下一个最大的数需要循环搜索,结果也是 2。
注意: 输入数组的长度不会超过 10000。
思路:时间O(n),空间O(n)
遍历数组,采用一个栈存储当前位置和当前值【i,nums[i]】。如果栈中最后一个元素的值小于当前数组遍历值,则将最后一个元素弹出,否则将当前位置和值存进栈中。
代码:
def nextGreaterElements(self, nums): """ :type nums: List[int] :rtype: List[int] """ if not nums: return nums m = len(nums) nums = nums + nums stack = [] res = [-1]*2*m for i in range(2*m): while stack and nums[i] > stack[-1][1]: last = stack.pop() res[last[0]] = nums[i] stack.append([i,nums[i]]) return res[:m]
二、题目:构成数组的一个maxTree
来自:《程序员代码面试指南》

解答:
对每一个元素,从左边和右边各选择第一个比这个元素大的值,选择值较小的元素作为父节点。
在【生成窗口最大数组】里面,已经掌握了,在O(N)时间复杂度里面,找到每个元素位置最近的比元素大的元素,同个这个套路,就可以构造一棵MaxTree了。
证明:
1 构造的不是森林
2 是一棵二叉树
证明:1
对于每一个树节点,都能往上找到一个节点,直到找到最大节点为止,这样所有树节点都有共同的父节点,这样构造出来的就是一棵树。
证明:2
使用反证法解决,如果是一棵二叉树,那么对于每个作为父节点的元素,能够在元素的一边找到两个或两个以上的元素。存在如:[p, b1, x, b2]这样的结构,p是父节点、b1、b2为子节点, x为其他节点。
- 按照题目,可以设定:
p > b1, p > b2 - 当b1 > b2:
b2不会选择p作为父节点,可能选择b1作为父节点. - 当b1 < b2:
当x < b2时,b1不会选择p作为父节点,选择b2作为父节点.
当x > b2时,b2不会选择p作为父节点,选择x作为父节点.
代码:
class Node: def __init__(self, value): self.value = value self.left = None self.right = None def getMaxTree(arr): nArr = [Node(arr[i]) for i in range(len(arr))] lBigMap = {} rBigMap = {} stack = [] for i in range(len(nArr)): curNode = nArr[i] while stack and stack[-1].value < curNode.value: cur = stack.pop() lBigMap[cur] = stack[-1] if stack else None rBigMap[cur] = curNode stack.append(curNode) while stack: cur = stack.pop() lBigMap[cur] = stack[-1] if stack else None rBigMap[cur] = None head = None for i in range(len(nArr)): curNode = nArr[i] left = lBigMap[curNode] right = rBigMap[curNode] if left == None and right == None: head = curNode elif left == None: if right.left == None: right.left = curNode else: right.right = curNode elif right == None: if left.left == None: left.left = curNode else: left.right = curNode else: parent = left if left.value < right.value else right if parent.left == None: parent.left = curNode else: parent.right = curNode return head arr = [3,4,5,1,2] getMaxTree(arr)
三、题目:求最大子矩阵的大小

思路:时间复杂度:O(N*M)
1、对每一行的1进行一个统计:

2、对每一行统计后的1来求最大矩形面积。【重要部分】

找到当前元素左边第一个比它小的索引以及右边第一个比它小的索引。


代码:
java:


python:
def Height(arr): if len(arr) == 0 or len(arr[0]) == 0: return 0 maxArea = 0 height = [0] * len(arr[0]) for i in range(len(arr)): for j in range(len(arr[0])): if arr[i][j] == 1: height[j] = height[j]+1 else: height[j] = 0 maxArea = max(maxArea,maxTan(height)) return maxArea def maxTan(height): stack = [] maxarea = 0 for i in range(len(height)): while stack and height[stack[-1]] >= height[i]: value = stack[-1] del stack[-1] k = -1 if not stack else stack[-1] area = (i-k-1) * height[value] maxarea = max(area,maxarea) stack.append(i) while stack: value = stack[-1] del stack[-1] k = -1 if not stack else stack[-1] area = (i-k) * height[value] maxarea = max(area,maxarea) return maxarea arr = [[1,0,1,0],[1,1,1,1],[1,1,1,0]] Height(arr)
四、题目:最大值减去最小值小于或等于num的子数组数量

思路:
采用两个栈 qmin 和 qmax 存储最大值和最小值。存储过程请参考上面三题。
子数组相当于滑动窗口。

代码:
def getMaxMin(arr,nums): if len(arr) == 0 or nums < 0: return 0 n = len(arr) qmin = [] qmax = [] res = 0 i , j = 0 , 0 while i < n: while j < n: while len(qmin) != 0 and arr[qmin[-1]] >= arr[j]: del qmin[-1] qmin.append(j) while len(qmax) != 0 and arr[qmax[-1]] <= arr[j]: del qmax[-1] qmax.append(j) if arr[qmax[0]] - arr[qmin[0]] > nums: break j += 1 if qmin[0] == i: del qmin[0] if qmax[0] == i: del qmax[0] res += j - i i += 1 return res arr = [8,7,12,5,16,9,17,2,4,6] nums = 3 res = getMaxMin(arr,nums)
五、题目:每日温度
根据每日 气温 列表,请重新生成一个列表,对应位置的输入是你需要再等待多久温度才会升高的天数。如果之后都不会升高,请输入 0 来代替。
例如,给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73],你的输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。
提示:气温 列表长度的范围是 [1, 30000]。每个气温的值的都是 [30, 100] 范围内的整数。
思路:
采用栈来存储,当前元素比栈最后一个大,则弹出栈最后一个元素,并将栈中最后一个元素的结果输入最终值列表中。
注意:栈中存储列表的值和索引。
代码:
def dailyTemperatures(self, temperatures): """ :type temperatures: List[int] :rtype: List[int] """ if len(temperatures)<=1: return [0] stack = [[temperatures[0],0]] res = [0] * len(temperatures) for i in range(1,len(temperatures)): while stack and stack[-1][0] < temperatures[i]: k,v = stack.pop() res[v] = i - v stack.append([temperatures[i],i]) return res
六:题目:132模式
给定一个整数序列:a1, a2, ..., an,一个132模式的子序列 ai, aj, ak 被定义为:当 i < j < k 时,ai < ak < aj。设计一个算法,当给定有 n 个数字的序列时,验证这个序列中是否含有132模式的子序列。
注意:n 的值小于15000。
示例1:
输入: [1, 2, 3, 4] 输出: False 解释: 序列中不存在132模式的子序列。
示例 2:
输入: [3, 1, 4, 2] 输出: True 解释: 序列中有 1 个132模式的子序列: [1, 4, 2].
示例 3:
输入: [-1, 3, 2, 0] 输出: True 解释: 序列中有 3 个132模式的的子序列: [-1, 3, 2], [-1, 3, 0] 和 [-1, 2, 0].
思路:时间O(n).空间O(n)
从后往前遍历:采用一个栈stack和third存储 ,third表示132模式中的2,stack存储比third大的数,只要找到比third小的数就返回True
若遇到比stack【-1】大的数,则将stack【-1】弹出,放入新的大的数
代码:
def find132pattern(self, nums): """ :type nums: List[int] :rtype: bool """ if len(nums)<3: return False stack = [] third = -10000000000 for i in range(len(nums)-1,-1,-1): if nums[i]<third: return True else: while stack and stack[-1]<nums[i]: third = stack.pop() stack.append(nums[i]) return False
七、题目:接雨水【栈】
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。 感谢 Marcos 贡献此图。
示例:
输入: [0,1,0,2,1,0,1,3,2,1,2,1] 输出: 6
思路1:
遍历列表,找到当前元素左边比它大的数【最大的一个】以及右边比它大的数【最大的一个】。
temp = min(左边最大,右边最大)-当前元素
结果 += temp if temp > 0 else 0
思路2:
def trap(height): max_level_l = 0 max_level_r = 0 res = 0 l = 0 r = len(height) - 1 #从左边和右边同时遍历,分两种情况 while l < r: #(1)如果左边当前元素 < 右边当前元素: if height[l] < height[r]: # 比较【左边最大值】 和 【左边当前元素】,若当前元素大,则最大值等于当前值 if height[l] > max_level_l: max_level_l = height[l] #若左边最大值大,则 res += (左边最大值 - 左边当前元素) 。 else: res += max_level_l - height[l] #左边指针加1 l += 1 #(2)如果左边当前元素 >= 右边当前元素: else: if height[r] > max_level_r: max_level_r = height[r] else: res += max_level_r - height[r] r -= 1 return res height = [0,1,0,2,1,0,1,3,2,1,2,1] trap(height)
八、题目:去除重复字母
给定一个仅包含小写字母的字符串,去除字符串中重复的字母,使得每个字母只出现一次。需保证返回结果的字典序最小(要求不能打乱其他字符的相对位置)。
示例 1:
输入:"bcabc"输出:"abc"
示例 2:
输入:"cbacdcbc"输出:"acdb"
思路:
- 先Counter(字符串s) 。
- 栈中是升序的,如果 当前元素 <= 栈最后一个元素,且 Counter(栈最后一个元素)> 1 且当前元素不在栈中:
就删除栈最后一个元素
Counter(最后元素) -= 1
- 如果当前元素不在栈中,则将其加入栈中。【即大于栈最后一个元素,后者处理完上述情况也要将当前元素加入栈中】
- 如果当前元素在栈中,则不加栈,但Counter(当前元素)-= 1
代码:
def removeDuplicateLetters(self, s): """ :type s: str :rtype: str """ if not s: return "" counter = Counter(s) stack = [] for ss in s: if not stack: stack.append(ss) else: while stack and stack[-1] >= ss and counter[stack[-1]] > 1 and ss not in stack: value = stack.pop() # stack.append(ss) counter[value] -= 1 if ss not in stack: stack.append(ss) else: counter[ss] -= 1 return "".join(stack)
RMQ问题:在一个数组区间中找最小值。
题目:二维数组,有两列,第一列为坐标,第二列为价值,如 [[1,1],[3,5],[4,8],[6,4],[10,3],[11,10],[12,8]] ,坐标差值>=d,求两个满足条件的坐标点价值最大为多少?
思路:将坐标排序,一个pre记录前面的最大值,一个 i 表示一个当前的指针,一个pos表示与 i 距离超过d的第一个位置指针,相当于记录后面的最大值。
代码:
def solve(arr,d): arr.sort(); suffix = [0] * len(arr) suffix[len(arr) - 1] = arr[len(arr) - 1][1] for i in range(len(arr) - 2,-1,-1): suffix[i] = arr[i][1] prefix = 0 pos = 0 ret = 0 for i in range(len(arr)-1): prefix = prefix if prefix > arr[i][1] else arr[i][1] while pos < len(arr)-1 and arr[pos][0] - arr[i][0] < d: pos += 1 if pos < len(arr): ret = ret if ret > prefix +suffix[pos] else prefix + suffix[pos] return ret arr = [[1,1],[3,5],[4,8],[6,4],[10,3],[11,10],[12,8]] d = 3 solve(arr,d)

