树（2）-----leetcode(层、深度、节点)

1、树的类实现：

class TreeNode(object):
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

2、最大深度：（递归）

    def maxDepth(root):
        """
        :type root: TreeNode
        :rtype: int
        """
        
        if root:
            left=maxDepth(root.left)
            right=maxDepth(root.right)
            return 1+max(left,right)
        return 0

3、交换左右子树：

（1）递归实现

def invertTree(self, root):
    if root:
        root.left, root.right = self.invertTree(root.right), self.invertTree(root.left)
        return root

（2）栈实现

def invertTree(self, root):
    stack = [root]
    while stack:
        node = stack.pop()
        if node:
            node.left, node.right = node.right, node.left
            stack += node.left, node.right
    return root

4、求树的每层平均值：

(1)（DFS深度优先遍历）

class TreeNode:
    def __init__(self,root):
        self.val=root
        self.left=None
        self.right=None

class Solution:
    def averageOfLevels(self, root):
        #root为TreeNode类型
        def computeSum(root,height,sumlist,countlist):
            if not root:
                return 0
            if height>=len(countlist):
                sumlist.append(0)
                countlist.append(0)
            sumlist[height]+=root.val
            countlist[height]+=1
            computeSum(root.left,height+1,sumlist,countlist)
            computeSum(root.right,height+1，sumlist,countlist)
        sumlist=[]
        countlist=[]
        computeSum(root,0,sumlist,countlist)
        return [i/j if j!=0 else 0 for i,j in zip(sumlist,countlist)]

(2)（BFS广度优先搜索）

def BFS（root):
       if not root:
            return 0
        prev,res=[root],[]
        while prev:
             cur=[]
            #给结果添加当前层数prev的平均值，prev为当前所有的值
            val=sum([node.val for node in prev])/float(len(prev))
            res.append(val)
            #该循环主要是cur添加prev所有的左右子树，即cur为下一层所有的值
            while prev:
                node=prev.pop()
                if node.left:
                    cur.append(node.left)
                if node.right:
                    cur.append(node.right)
            #将当前层数变为下一层
            prev=cur        
        return res

5、判断两颗树是否相同（递归）

def isSameTrees(p,q):
    if not p and not q:
        return True    
    elif p and not q or (q and not p):
        return False
    else:
        if p.val!=q.val:
            return False
        else:
            return isSameTrees(p.left,q.left) and isSameTrees(p.right,q.right)

6、输出树的所有路径：(前序遍历，深度遍历的特例）

def allPath(root):
    '''
    root为TreeNode类
    输出：['1->2->5','1->3']
    '''
    res=[]
　　 strPre=''
    def helper(Tree,strPre):
        if Tree:
            strPre+=str(Tree.val)+'->'
　　　　　　　　#若左右子树都为空的时候就把结果加入列表中

            if not Tree.left and not Tree.right:
                res.append(strPre[:-2])
　　　　　　　　#否则递归将左右子树的路径加进来
            else:
                helper(Tree.left,strPre)
                helper(Tree.right,strPre)
    helper(root,strPre)
    return res

7、二叉树的层次遍历：（BFS）

    def levelOrder(self, root):
        """
        :type root: TreeNode
        :rtype: List[List[int]]
        """
        res=[]
        if not root:
            return []
        prev=[root]
        while prev:           
            temp=[node.val for node in prev]
            res.append(temp)
            cur=[]
            while prev:
                node=prev.pop(False)  
                if node.left:
                    cur.append(node.left)                 
                if node.right:
                    cur.append(node.right)
            prev=cur
        return res

#反向层次遍历
# dfs recursively
def levelOrderBottom1(self, root):
    res = []
    self.dfs(root, 0, res)
    return res

def dfs(self, root, level, res):
    if root:
        if len(res) < level + 1:
            res.insert(0, [])
        res[-(level+1)].append(root.val)
        self.dfs(root.left, level+1, res)
        self.dfs(root.right, level+1, res)
        
# dfs + stack
def levelOrderBottom2(self, root):
    stack = [(root, 0)]
    res = []
    while stack:
        node, level = stack.pop()
        if node:
            if len(res) < level+1:
                res.insert(0, [])
            res[-(level+1)].append(node.val)
            stack.append((node.right, level+1))
            stack.append((node.left, level+1))
    return res
 
# bfs + queue   
def levelOrderBottom(self, root):
    queue, res = collections.deque([(root, 0)]), []
    while queue:
        node, level = queue.popleft()
        if node:
            if len(res) < level+1:
                res.insert(0, [])
            res[-(level+1)].append(node.val)
            queue.append((node.left, level+1))
            queue.append((node.right, level+1))
    return res

8、将有序数组转换为二叉搜索树（递归）

# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def sortedArrayToBST(self, nums):
        """
        :type nums: List[int]
        :rtype: TreeNode
        """
        if not nums:
            return None
        k=len(nums)//2
        root=TreeNode(nums[k])
        root.left=self.sortedArrayToBST(nums[:k])
        root.right=self.sortedArrayToBST(nums[k+1:])
        return root

9、求树的坡度（递归，注意实例变量和静态变量的使用）

给定一个二叉树，计算整个树的坡度。

一个树的节点的坡度定义即为，该节点左子树的结点之和和右子树结点之和的差的绝对值。空结点的的坡度是0。

整个树的坡度就是其所有节点的坡度之和。

示例:

输入: 
         1
       /   \
      2     3
输出: 1
解释: 
结点的坡度 2 : 0
结点的坡度 3 : 0
结点的坡度 1 : |2-3| = 1
树的坡度 : 0 + 0 + 1 = 1

class Solution(object):   
    tilt=0
    def findTilt(self, root):   
        """
        :type root: TreeNode
        :rtype: int
        """
     
        def helper(root):
            if not root:
                return 0
            left=helper(root.left)
            right=helper(root.right)
            self.tilt+=abs(left-right)
            return left+right+root.val
        helper(root)
        return self.tilt

10、把二叉搜索树转换为累加树（递归，注意静态变量和实例变量的运用）

给定一个二叉搜索树（Binary Search Tree），把它转换成为累加树（Greater Tree)，使得每个节点的值是原来的节点值加上所有大于它的节点值之和。

例如：

输入: 二叉搜索树:
              5
            /   \
           2     13

输出: 转换为累加树:
             18
            /   \
          20     13

class Solution(object):    
    sumval=0
    def convertBST(self, root):
        """
        :type root: TreeNode
        :rtype: TreeNode
        """           
        if not root:
            return None       
        def helper(node):
            if node:
                helper(node.right)
                node.val+=self.sumval
                self.sumval=node.val
                helper(node.left)
            return node
        root=helper(root)
        return root

11、二叉树中的第二小的节点（BFS、DFS）

    def findSecondMinimumValue(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if not root:
            return -1
        prev=[root]
        minVal=root.val
        secondVal=float('inf')
        while prev:
            cur=[]
            while prev:
                node=prev.pop()
                if minVal<node.val and node.val<secondVal:
                    secondVal=node.val
                if node.left:
                    cur.append(node.left)
                if node.right:
                    cur.append(node.right)
            prev=cur
        return -1 if secondVal==float('inf') else secondVal

12、判断一棵树是否为高度平衡二叉树：（递归）

高度平衡二叉树的定义是一个二叉树的每个节点的左右子树的高度差绝对值不超过1。

思路1：

先介绍自己的蠢办法，先写一个求树高度的函数，然后遍历所有节点（求其左右子树的高度，然后作差，判断是否在1之内）

【求高度函数：递归】

【遍历节点：用栈】

class Solution(object):
    def isBalanced(self, root):
        """
        :type root: TreeNode
        :rtype: bool
        """
        if not root:
            return True
        def helper(root):
            if root:
                left=helper(root.left)
                right=helper(root.right)
                return 1+max(left,right)
            return 0
        prev=[root]
        while prev:
            cur=[]
            while prev:
                node=prev.pop()
                left=right=0
                if node.left:
                    cur.append(node.left)
                    left=helper(node.left)
                if node.right:
                    cur.append(node.right)
                    right=helper(node.right)
                if abs(left-right)>1:
                    return False
            prev=cur
        return True

思路2：直接递归求高度，在计算高度时顺便计算左右子树的高度差，不合格就返回错误】（DFS）

https://leetcode.com/problems/balanced-binary-tree/discuss/128678/Python-3-iterative-and-recursive-solution

    def isBalanced(self, root):
        """
        :type root: TreeNode
        :rtype: bool
        """
        def helper(root):
            if not root:
                return 0
            left=helper(root.left)
            right=helper(root.right)
            if left==-1 or right==-1 or abs(left-right)>1:
                return -1
            return 1+max(left,right)
        res=helper(root)
        return False if res==-1 else True

思路3：用BFS来求解

13、路径求和（两个递归求解）：

给定一个二叉树，它的每个结点都存放着一个整数值。

找出路径和等于给定数值的路径总数。

路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

二叉树不超过1000个节点，且节点数值范围是 [-1000000,1000000] 的整数。

示例：

root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8

      10
     /  \
    5   -3
   / \    \
  3   2   11
 / \   \
3  -2   1

返回 3。和等于 8 的路径有:

1.  5 -> 3
2.  5 -> 2 -> 1
3.  -3 -> 11

class Solution(object):
    def pathSum(self, root, sum):
        """
        :type root: TreeNode
        :type sum: int
        :rtype: int
        """     
        self.res=0
        def ans(root,cur,sum):
            cur+=root.val
            if cur==sum:
                self.res+=1
            if root.left:
                ans(root.left,cur,sum)
            if root.right:
                ans(root.right,cur,sum)
        def helper(root,sum):
            if root:
                ans(root,0,sum)
                if root.left:
                    helper(root.left,sum)
                if root.right:
                    helper(root.right,sum)
        helper(root,sum)
        return self.res

14、路径总和（递归）【用列表的深拷贝】

    def pathSum(self, root, sum):
        """
        :type root: TreeNode
        :type sum: int
        :rtype: List[List[int]]
        """
        if not root:
            return []
        res=[]
        temp= []
        def helper(root,sum,temp,res):
            if root:
                # temp += str(root.val) + ','
                temp.append(root.val)
                if not root.left and not root.right:
                    # temp = temp.split(',')[:-1]
                    # temp = map(lambda x: int(x), temp)
                    a=reduce(lambda x,y:x+y,temp)
                    if a==sum:
                        res.append(temp)
                else:
                    temp_copy = copy.deepcopy(temp)
                    helper(root.left,sum,temp_copy,res)
                    helper(root.right,sum,temp,res)
        helper(root,sum,temp,res)
        return res

15、二叉树剪枝（递归）

给定二叉树根结点 root ，此外树的每个结点的值要么是 0，要么是 1。

返回移除了所有不包含 1 的子树的原二叉树。

( 节点 X 的子树为 X 本身，以及所有 X 的后代。)

示例1:
输入: [1,null,0,0,1]
输出: [1,null,0,null,1]
 
解释: 
只有红色节点满足条件“所有不包含 1 的子树”。
右图为返回的答案。

示例2:
输入: [1,0,1,0,0,0,1]
输出: [1,null,1,null,1]

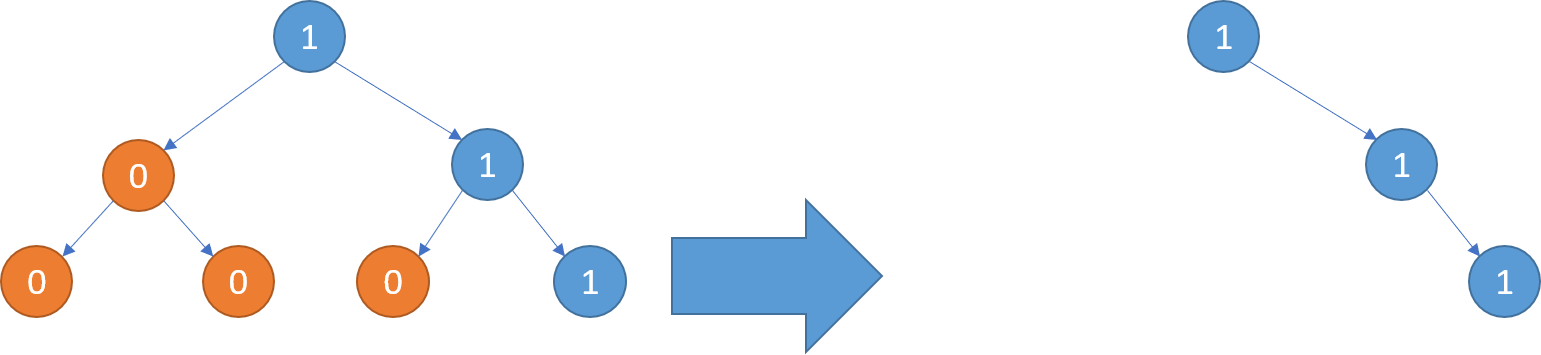
示例3:
输入: [1,1,0,1,1,0,1,0]
输出: [1,1,0,1,1,null,1]

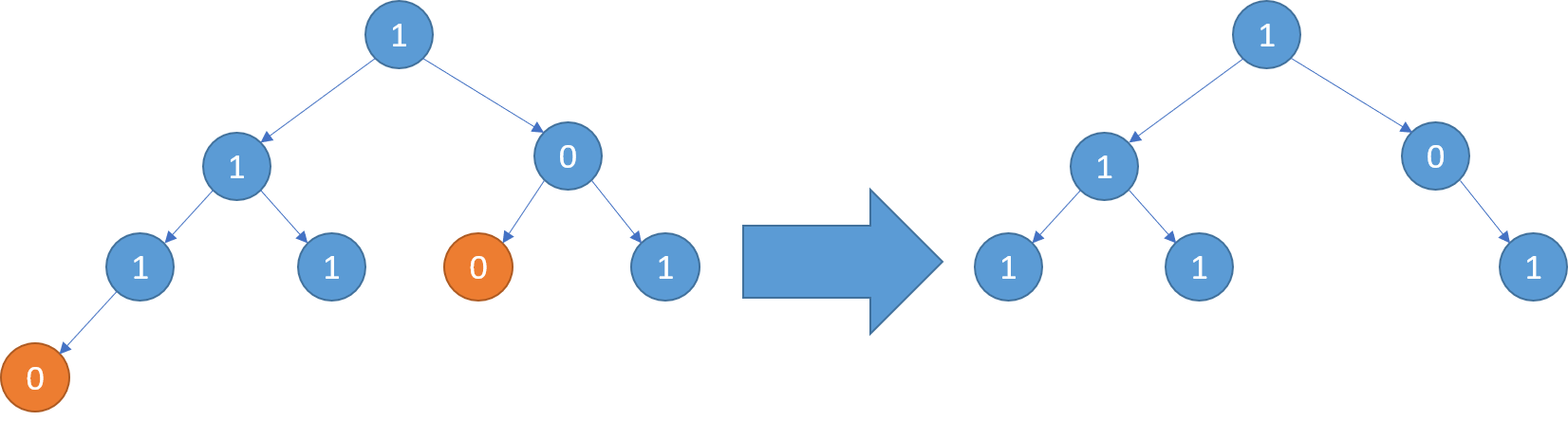
说明:

给定的二叉树最多有 100 个节点。
每个节点的值只会为 0 或 1 。

    def pruneTree(self, root):
        """
        :type root: TreeNode
        :rtype: TreeNode
        """
        if not root:
            return
        
        root.left, root.right = self.pruneTree(root.left), self.pruneTree(root.right)
        return root if any([root.val, root.left, root.right]) else None

    def pruneTree(self, root):
        """
        :type root: TreeNode
        :rtype: TreeNode
        """
        if root:
            root.left=self.pruneTree(root.left)
            root.right=self.pruneTree(root.right)
            if not root.left and not root.right and root.val==0:
                root=None
            else:
                return root
        return None

16、输出二叉树：【递归，重点在建立一个矩阵】

在一个 m*n 的二维字符串数组中输出二叉树，并遵守以下规则：

行数 m 应当等于给定二叉树的高度。
列数 n 应当总是奇数。
根节点的值（以字符串格式给出）应当放在可放置的第一行正中间。根节点所在的行与列会将剩余空间划分为两部分（左下部分和右下部分）。你应该将左子树输出在左下部分，右子树输出在右下部分。左下和右下部分应当有相同的大小。即使一个子树为空而另一个非空，你不需要为空的子树输出任何东西，但仍需要为另一个子树留出足够的空间。然而，如果两个子树都为空则不需要为它们留出任何空间。
每个未使用的空间应包含一个空的字符串""。
使用相同的规则输出子树。

示例 1:

输入:
     1
    /
   2
输出:
[["", "1", ""],
 ["2", "", ""]]

示例 2:

输入:
     1
    / \
   2   3
    \
     4
输出:
[["", "", "", "1", "", "", ""],
 ["", "2", "", "", "", "3", ""],
 ["", "", "4", "", "", "", ""]]

示例 3:

输入:
      1
     / \
    2   5
   / 
  3 
 / 
4 
输出:
[["",  "",  "", "",  "", "", "", "1", "",  "",  "",  "",  "", "", ""]
 ["",  "",  "", "2", "", "", "", "",  "",  "",  "",  "5", "", "", ""]
 ["",  "3", "", "",  "", "", "", "",  "",  "",  "",  "",  "", "", ""]
 ["4", "",  "", "",  "", "", "", "",  "",  "",  "",  "",  "", "", ""]]

注意: 二叉树的高度在范围 [1, 10] 中。

class Solution(object):
    def printTree(self, root):
        """
        :type root: TreeNode
        :rtype: List[List[str]]
        """
        h=self.height(root)
        matrix=[['' for m in range(2**h-1)] for n in range(h)]
        self.makeMatrix(root,matrix,0,(2**h)-1,0)
        return matrix
    def height(self, node):
        return max(1 + self.height(node.left), 1 + self.height(node.right)) if node else 0
    def makeMatrix(self,root,matrix,col1,col2,h):
        if root:
            i=(col1+col2)//2
            matrix[h][i]=str(root.val)
            self.makeMatrix(root.left,matrix,col1,i-1,h+1)
            self.makeMatrix(root.right,matrix,i+1,col2,h+1)

17、二叉树展开为链表【递归，重点在原地改动树的结构，需要额外的栈来存储树节点原本的值】

例如，给定二叉树

将其展开为：

    def flatten(self,root):
        """
        :type root: TreeNode
        :rtype: voi       
 #原地改动，全部取出节点到列表中，再从列表中改动成树     

        listTree=[]
        def helper(root):
            if root:
                listTree.append(root)
                helper(root.left)
                helper(root.right)
        helper(root)
        for i in range(len(listTree)):
            if i<len(listTree)-1:
                listTree[i].right=listTree[i+1]
                listTree[i].left=None

        #原地改动，将树的右节点放在栈中，将树的左节点变成树的右节点
        stack=[]
        def helper(root):
            if root:
                if root.right:
                    stack.append(root.right)
                if root.left:
                    root.right=root.left
                    root.left=None
                elif not root.left and stack:
                    root.right=stack.pop()
                helper(root.right)
        helper(root)

18、寻找重复的子树

给定一棵二叉树，返回所有重复的子树。对于同一类的重复子树，你只需要返回其中任意一棵的根结点即可。

两棵树重复是指它们具有相同的结构以及相同的结点值。

示例 1：

下面是两个重复的子树：

      2
     /
    4

和

因此，你需要以列表的形式返回上述重复子树的根结点。

思路1：（先遍历所有的节点存在列表中，列表每个节点两两之间比较一下，是否是同一颗树，如果是就将该节点放入结果中，最后也要注意一下去重）【这个方法被我写得超出时间限制】

思路2：（先遍历所有的节点存在列表中，然后将每个节点对应的先序遍历存在另一个列表中，然后用一个字典存两个列表，先序遍历的列表作为key，节点列表作为value，若key有重复的，就将字典值加进结果，去重就可以了。）

from collections import defaultdict
class Solution(object):
    def findDuplicateSubtrees(self, root):
        """
        :type root: TreeNode
        :rtype: List[TreeNode]
        """


        #思路1：超出时间限制


        if not root:
            return []
        listNode=[]
        def isSameTree(p,q):
            if not p and not q:
                return True
            elif (p and not q) or (q and not p):
                return False
            else:
                if p.val!=q.val:
                    return False
                else:
                    return isSameTree(p.left,q.left) and isSameTree(p.right,q.right)                    
        prev=[root]
        while prev:
            node=prev.pop(0)
            if node:
                listNode.append(node)
                prev.extend([node.left,node.right])
        res=[]
        i=0
        
        while i < len(listNode):
            j=i+1
            flag=1
            while i+1 <= j < len(listNode):
                if isSameTree(listNode[i],listNode[j]):
                    if listNode[i] not in res:
                        res.append(listNode[i])
                    del listNode[j]
                    flag=0
                if flag:
                    j+=1
                flag=1
            i+=1
        return res
    

        #思路2


        if not root:
            return []
        def order(root):
            orderRes=[]
            prev=[root]
            while prev:
                node=prev.pop()
                if node:
                    orderRes.append(node.val)
                    prev.extend([node.left,node.right])
                else:
                    orderRes.append(None)
            return orderRes
        prev=[root]
        dic=defaultdict(TreeNode)
        res=[]
        while prev:
            node=prev.pop()
            if node:
                if tuple(order(node)) not in dic:
                    dic[tuple(order(node))]=node
                else:
                    res.append(dic[tuple(order(node))])
                prev.extend([node.left,node.right])
        return list(set(res))

19、验证二叉搜索树【递归，左子树所有节点都小于根节点，右子树所有节点都大于根节点，则返回正。】用两个循环或者两个递归

    def isValidBST(self, root):
        """
        :type root: TreeNode
        :rtype: bool
        """
        if not root:
            return True
        def compare(root,value,flag):
            if not root:
                return True
            stack=[root]
            while stack:
                node=stack.pop()
                if node:
                    if flag==1:
                        if node.val>=value:
                            return False
                    else:
                        if node.val<=value:
                            return False
                    stack.extend([node.left,node.right])
            return True
        if compare(root.left,root.val,1) and compare(root.right,root.val,0):
            return self.isValidBST(root.left) and self.isValidBST(root.right)
        else:
            return False

20、二叉树最大宽度【遍历整颗树，每个节点标记序号，每层最大节点减去最小节点的值+1----为结果】

给定一个二叉树，编写一个函数来获取这个树的最大宽度。树的宽度是所有层中的最大宽度。这个二叉树与满二叉树（full binary tree）结构相同，但一些节点为空。

每一层的宽度被定义为两个端点（该层最左和最右的非空节点，两端点间的null节点也计入长度）之间的长度。

示例 1:

输入: 

           1
         /   \
        3     2
       / \     \  
      5   3     9 

输出: 4
解释: 最大值出现在树的第 3 层，宽度为 4 (5,3,null,9)。

示例 2:

输入: 

          1
         /  
        3    
       / \       
      5   3     

输出: 2
解释: 最大值出现在树的第 3 层，宽度为 2 (5,3)。

示例 3:

输入: 

          1
         / \
        3   2 
       /        
      5      

输出: 2
解释: 最大值出现在树的第 2 层，宽度为 2 (3,2)。

示例 4:

输入: 

          1
         / \
        3   2
       /     \  
      5       9 
     /         \
    6           7
输出: 8
解释: 最大值出现在树的第 4 层，宽度为 8 (6,null,null,null,null,null,null,7)。

注意: 答案在32位有符号整数的表示范围内。

    def widthOfBinaryTree(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if not root:
            return 0
        prev,temp=[(root,1)],[]
        res=[]
        while prev:
            cur=[]
            while prev:
                node,index=prev.pop(0)
                temp.append(index)
                if node:
                    if node.left:
                        cur.append((node.left,index*2-1))
                    if node.right:
                        cur.append((node.right,index*2))
            res.append(max(temp)-min(temp))
            temp=[]
            prev=cur
        return max(res)+1

21、建立所有不同的二叉搜索树【思想：遍历+递归，用生成器实现】

class TreeNode(object):
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None
def _gen_trees(start, end):
    if start > end:
        yield None
    for j in range(start, end+1):
        for l_tree in _gen_trees(start, j-1):
            for r_tree in _gen_trees(j+1, end):
                root = TreeNode(j)
                root.left = l_tree
                root.right = r_tree
                yield root
def generateTrees(n):
    if n == 0:
        return []
    return list(_gen_trees(1, n)

【思想：遍历+递归，用列表存结果】

    def bulidTree(self,listn):
        if not listn:
            return [None]
        res = []
        for k, item in enumerate(listn):
            root = TreeNode(item)
            left = self.bulidTree(listn[:k])
            right = self.bulidTree(listn[k + 1:])
            for i in range(len(left)):
                for j in range(len(right)):
                    new_root = copy.deepcopy(root)
                    if left[i] is not None and right[j] is not None:
                        new_root.left = left[i]
                        new_root.right = right[j]
                        res.append(new_root)
                    elif left[i] is not None and right[j] is None:
                        new_root.left = left[i]
                        res.append(new_root)
                    elif left[i] is None and right[j] is not None:
                        new_root.right = right[j]
                        res.append(new_root)
            if res == []:
                res.append(root)
        return res

22、所有可能的完整二叉树【遍历+递归】

完整二叉树是一类二叉树，其中每个结点恰好有 0 或 2 个子结点。

返回包含 N 个结点的所有可能完整二叉树的列表。答案的每个元素都是一个可能树的根结点。

答案中每个树的每个结点都必须有 node.val=0。

你可以按任何顺序返回树的最终列表。

示例：

输入：7
输出：[[0,0,0,null,null,0,0,null,null,0,0],[0,0,0,null,null,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,null,null,null,null,0,0],[0,0,0,0,0,null,null,0,0]]
解释：

提示：

1 <= N <= 20

代码：

    def allPossibleFBT(self, N):
        """
        :type N: int
        :rtype: List[TreeNode]
        """
        if N == 1:
            return [TreeNode(0)]
        res = []
        for nleft,nright in [(i,N-1-i) for i in range(1,N,2)]:
            for left in self.allPossibleFBT(nleft):
                for right in self.allPossibleFBT(nright):
                    root = TreeNode(0)
                    root.left = left
                    root.right = right
                    res.append(root)
        return res

23、二叉搜索树-----依次输出最小值【迭代器】

实现一个二叉搜索树迭代器。你将使用二叉搜索树的根节点初始化迭代器。

调用 next() 将返回二叉搜索树中的下一个最小的数。

注意:next() 和hasNext() 操作的时间复杂度是O(1)，并使用 O(h) 内存，其中 h 是树的高度。

class BSTIterator(object):
    def __init__(self, root):
        """
        :type root: TreeNode
        """
        self.stack=[]
        while root:
            self.stack.append(root)
            root=root.left
                
    
    def hasNext(self):
        """
        :rtype: bool
        """
        return len(self.stack)>0
        

    def next(self):
        """
        :rtype: int
        """
        node=self.stack.pop()
        x=node.right
        while x:
            self.stack.append(x)
            x=x.left
        return node.val

24、二叉树增加一行【BFS实现】

给定一个二叉树，根节点为第1层，深度为 1。在其第 d 层追加一行值为 v 的节点。

添加规则：给定一个深度值 d （正整数），针对深度为 d-1 层的每一非空节点 N，为 N 创建两个值为 v 的左子树和右子树。

将 N 原先的左子树，连接为新节点 v 的左子树；将 N 原先的右子树，连接为新节点 v 的右子树。

如果 d 的值为 1，深度 d - 1 不存在，则创建一个新的根节点 v，原先的整棵树将作为 v 的左子树。

示例 1:

示例 2:

注意:

输入的深度值 d 的范围是：[1，二叉树最大深度 + 1]。
输入的二叉树至少有一个节点。

class Solution(object):
    def addOneRow(self, root, v, d):
        """
        :type root: TreeNode
        :type v: int
        :type d: int
        :rtype: TreeNode
        """
        
        if root and d==1:
            node=TreeNode(v)
            node.left=root
            return node        
        
        prev=[root]
        h=1
        while prev:
            cur=[]           
            while prev:
                node=prev.pop(0)

                if h==d-1:
                    copy_left=node.left
                    copy_right=node.right
                    node.left=TreeNode(v)
                    node.left.left=copy_left
                    node.right=TreeNode(v)
                    node.right.right=copy_right
                else:
                    if node.left:
                        cur.append(node.left)
                    if node.right:
                        cur.append(node.right)
            h+=1
            prev=cur
        return root

25、二叉树最近公共祖先

思路：从根节点开始遍历，如果node1和node2中的任一个和root匹配，那么root就是最低公共祖先。如果都不匹配，则分别递归左、右子树，如果有一个节点出现在左子树，并且另一个节点出现在右子树，则root就是最低公共祖先. 如果两个节点都出现在左子树，则说明最低公共祖先在左子树中，否则在右子树。

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]

        _______3______
       /              \
    ___5__          ___1__
   /      \        /      \
   6      _2       0       8
         /  \
         7   4

示例 1:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。

示例 2:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。

    def lowestCommonAncestor(self, root, p, q):
        """
        :type root: TreeNode
        :type p: TreeNode
        :type q: TreeNode
        :rtype: TreeNode
        """
        if p==root or q==root or root==None:
            return root
        else:
            left=self.lowestCommonAncestor(root.left, p, q)
            right=self.lowestCommonAncestor(root.right, p, q)
            if left and not right:
                return left
            elif not left and right:
                return right
            elif left and right:
                return root

posted on 2018-05-17 12:53 吱吱了了阅读(497) 评论(0) 编辑收藏举报

刷新页面返回顶部