十大排序
一、十大排序总结
https://www.cnblogs.com/guoyaohua/p/8600214.html总结得很好。
1、原地排序:快速排序、堆排序、插入排序、冒泡排序、希尔排序、直接选择排序
2、非原地排序:归并排序、计数排序、基数排序、桶排序
3、对有序的序列排序:冒泡、直接插入
4、对无序的序列排序:快排
5、对大数据排序:O(nlog(n))都比较好,快排、堆排、归并【归并稳定、快排和堆排不稳定】
6、
7、常见的快速排序、归并排序、堆排序、冒泡排序等属于比较排序。
计数排序、基数排序、桶排序则属于非比较排序。
8、算法复杂度与初始状态无关的排序算法有:选择排序、堆排、归并、基数(一堆乌龟选基友)
元素总比较次数与初始状态无关的有:选择排序、基数排序。
元素总移动次数与初始状态无关的有:归并排序、基数排序。
9、稳定的排序:冒泡、插入、归并、计数、桶、基数
【稳定性:相同的数字其索引位置也有序,即且在原本的列表中 出现在 之前,在排序过的列表中 也将会是在 之前。】
不稳定的排序:选择、希尔、快排、堆排(一堆好东西需要快速 选择和share)

二、冒泡排序:
比较相邻的两项,交换顺序排错的项。每对列表实行一次遍历,就有一个最大项排在了正确的位置。第二次遍历开始时,最大的数据项已经归位。
1、未改进的冒泡排序:两个循环
def bubbleSort(nums): for num in range(len(nums)-1,0,-1): for i in range(num): if nums[i]>nums[i+1]: temp=nums[i+1] nums[i+1]=nums[i] nums[i]=temp
2、改进的冒泡排序:
只要在某一次排完序之后顺序是正确的,那么就停止排序。【设置一个标记,如果顺序正确就停止遍历】
def bubbleSort(nums): n=len(nums)-1 exit=True while n>0 and exit: exit=False for i in range(n): if nums[i]>nums[i+1]: exit=True temp=nums[i+1] nums[i+1]=nums[i] nums[i]=temp n-=1
三、选择排序
就是最普通那种思路,找到最大的往最右换,接着找到次大的再往右换。
def selectionSort(nums): n=len(nums)-1 for i in range(n,0,-1): maxIndex=0 for j in range(i+1): if nums[j]>nums[maxIndex]: maxIndex=j temp=nums[i] nums[i]=nums[maxIndex] nums[maxIndex]=temp
四、插入排序
从前往后来遍历数,新的数据和前面的已经排好的子表进行比较插入到正确的位置。
def insertSort(nums): for i,num in enumerate(nums): position=i while position>0 and nums[position-1]>num: nums[position]=nums[position-1] position=position-1 nums[position]=num
def insertsort(arr): if not arr: return arr for i in range(len(arr)): for j in range(i): if arr[j] > arr[i]: arr[i],arr[j] = arr[j],arr[i] return arr if __name__ =='__main__': arr = [43,4,12,4,6,9]
五、希尔排序
希尔排序是简单插入排序的改进,shell排序是相当于把一个数组中的所有元素分成几部分来排序;先把几个小部分的元素排序好,让元素大概有个顺序,最后再全面使用插入排序。一般最后一次排序都是和上面的插入排序一样的;

对于下标为【0】【3】【6】【9】的数据即【5】【12】【9】【7】来分割,
【5】【12】【9】【7】为一组,【16】【3】【17】为一组,【20】【8】【19】为一组。三组进分别行直接插入排序进行交换,结果为
【5】【7】【9】【12】,【3】【16】【17】,【8】【19】【20】,三组数据是在原本的位置即【5】【3】【8】【7】【16】【19】【9】【17】【20】【12】
代码:
def shell_sort(lists): if not lists: return lists n = len(lists) gap = n // 2 while gap > 0: ###以下是插入排序 for i in range(gap, n): temp = lists[i] preIndex = i - gap while preIndex >= 0 and lists[preIndex] > temp: lists[preIndex + gap] = lists[preIndex] preIndex -= gap lists[preIndex + gap] = temp gap //= 2 return lists if __name__ == '__main__': arr = [3, 5, 15, 26, 2, 27, 4, 19, 36, 50, 12] res = shell_sort(arr) print(res)
六、快速排序
快速排序的基本思想是,通过一轮的排序将序列分割成独立的两部分,其中一部分序列的关键字(这里主要用值来表示)均比另一部分关键字小。继续递归对长度较短的序列进行同样的分割,最后到达整体有序。在排序过程中,由于已经分开的两部分的元素不需要进行比较,故减少了比较次数,降低了排序时间。
|
平均时间:O(nlogn) |
平均空间:O(nlogn) |
|
最好时间:O(nlogn)
|
|
| 最坏时间:O(n2) | 最坏空间:O(n) |
最坏情况的发生是在数组有序且为完全逆序时,此时快排退化成冒泡;
解决方法:随机取主元或者取中位数,三路快排(解决大量重复数据)
def quick_sort(arr,l,r): if l < r: q = partition(arr,l,r) quick_sort(arr,l,q-1) quick_sort(arr,q+1,r) def partition(arr,l,r): x = arr[r] i = l-1 for j in range(l,r): if arr[j] < x: i += 1 arr[i],arr[j] = arr[j],arr[i] arr[i+1] , arr[r] = arr[r] ,arr[i+1] return i+1
随机选择主元,二路快排
import random def quick_sort(arr , l , r): if len(arr) <= 1: return arr if l < r: p = partition(arr, l , r) quick_sort(arr, l , p - 1) quick_sort(arr, p + 1 , r) def partition(arr,l,r): if l < r: ###randint是生成l<=index<=r的随机整数 ##随机生成主元 index = random.randint(l,r) x = arr[index] arr[r],arr[index] = arr[index],arr[r] i = l - 1 for j in range(l,r): if arr[j] < x: i += 1 arr[i] , arr[j] = arr[j] , arr[i] arr[i+1],arr[r] = arr[r],arr[i+1] return i + 1 arr = [1,3,4,6,2,7] quick_sort(arr , 0 , len(arr)-1) print(arr)
双路快排和三路快排:
三路快排优点:解决了近乎有序的数组和有大量重复数组的元素排序问题


三路快排的代码:
import random #三路排序 def partition(arr,pivot,l,r): if not arr: return arr small ,index , big = l-1 , l , r+1 while index != big: if arr[index] < pivot: small += 1 arr[small] , arr[index] = arr[index] , arr[small] index += 1 elif arr[index] == pivot: index += 1 else: big -= 1 arr[big] , arr[index] = arr[index] , arr[big] return small,big #快排,随机选取主元 def quick_sort(arr,l,r): if len(arr) <= 1: return arr pivot = random.sample(arr,1)[0] if l < r: l1,r1 = partition(arr,pivot,l,r) quick_sort(arr,l,l1) quick_sort(arr,r1,r) return arr if __name__=='__main__': arr = [9,0,1,3,4,3,1] res = quick_sort(arr,0,len(arr)-1) print(res) if __name__=='__main__': arr = [9,0,1,3,4,3,1] res = quick_sort(arr,0,len(arr)-1) print(res)
七、堆排序
http://www.cnblogs.com/0zcl/p/6737944.html
先建立堆,然后排序。
满足堆的性质:子结点的键值或索引总是小于(或者大于)它的父节点。
7.1 算法描述
调整堆;
循环(条件:堆不为空){
取出堆顶元素;
将最后一个元素移动到堆顶位置;
调整使之再次成为堆;
}
例子:
给定一个列表array=[16,7,3,20,17,8],对其进行堆排序。
一、将列表中的数值构建成一个完全二叉树:

二、调整:初始化大顶堆,即将列表中的最大值放在堆顶。并且构建成堆。即父>=子。 初始化大顶堆时 是从最后一个有子节点开始往上调整最大堆。




三、交换:堆顶元素和堆尾【最后一个元素】交换,此时可以砍掉堆尾元素了,因为最大值已经排好序。而堆顶元素(最大数)与堆最后一个数交换后,需再次调整成大顶堆,此时是从上往下调整的。

四、重复步骤二、三,直到结束。即【重新调整剩余的堆并交换堆顶和堆尾的数【除了20之外的数】】。
(1)调整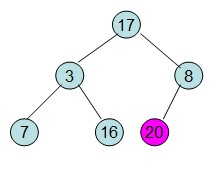
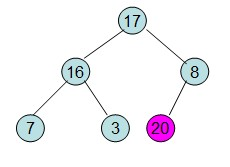 (2)交换
(2)交换
(1)调整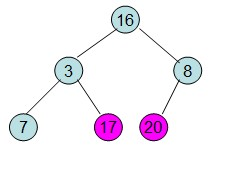
 (2)交换
(2)交换
(1)调整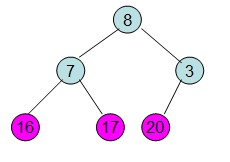 (2)交换
(2)交换
(1)调整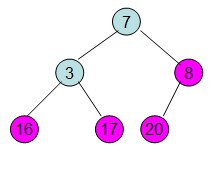 (2)交换
(2)交换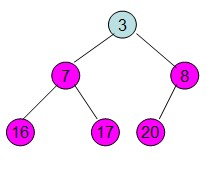
代码
#堆排序算法 #全局变量 n = 0 def heap_sort(arr): global n n = len(arr) if n <= 1 : return arr # 1、构建一个最大堆 buildMaxHeap(arr) # 2、循环将堆首(最大值)与末位交换,然后再重新调整最大堆 while n > 0: arr[0] , arr[n-1] = arr[n-1] , arr[0] n -= 1 adjustHeap(arr,0) return arr #建立最大堆 def buildMaxHeap(arr): global n for i in range(n//2-1,-1,-1): adjustHeap(arr,i) #调整成为最大堆 def adjustHeap(arr,i): global n maxIndex = i #如果有左子树,且左子树大于父节点,则将最大指针指向左子树 if i * 2 < n and arr[i * 2] > arr[maxIndex]: maxIndex = i * 2 # 如果有右子树,且右子树大于父节点,则将最大指针指向右子树 if i * 2 + 1 < n and arr[i*2 + 1] > arr[maxIndex]: maxIndex = i * 2 + 1 # 如果父节点不是最大值,则将父节点与最大值交换,并且递归调整与父节点交换的位置。 if maxIndex != i: arr[maxIndex] , arr[i] = arr[i] , arr[maxIndex] adjustHeap(arr,maxIndex) if __name__ == '__main__': #自己建堆 arr2 = [3, 5, 15, 26, 2, 27, 4, 19, 36, 50, 12] heap_sort(arr2) print(arr2) #[2, 3, 4, 5, 12, 15, 19, 26, 27, 36, 50]
八、归并排序
- 把长度为n的输入序列分成两个长度为n/2的子序列;
- 对这两个子序列分别采用归并排序;
- 将两个排序好的子序列合并成一个最终的排序序列。
#归并排序 def merge(left,right): if not left: return right if not right: return left arr = [] i,j = 0,0 while i < len(left) and j < len(right): if left[i] >= right[j]: arr.append(right[j]) j += 1 else: arr.append(left[i]) i += 1 arr += left[i:] arr += right[j:] return arr #合并两个子序列 def merge_sort(arr): if not arr or len(arr) == 1: return arr mid = len(arr) // 2 left = merge_sort(arr[:mid]) right = merge_sort(arr[mid:]) return merge(left,right) if __name__=="__main__": arr = [3, 5, 15, 26, 2, 27, 4, 19, 36, 50, 12] res = merge_sort(arr) print(res)
排序中topK那点事(转)
问题描述:有 N (N>1000000)个数,求出其中的前K个最小的数(又被称作topK问题)。
这类问题似乎是备受面试官的青睐,相信面试过互联网公司的同学都会遇到这来问题。下面由浅入深,分析一下这类问题。
思路1:【全部排序】
最基本的思路,将N个数进行完全排序,从中选出排在前K的元素即为所求。有了这个思路,我们可以选择相应的排序算法进行处理,快速排序,堆排序和归并排序都能达到O(NlogN)的时间复杂度。当然,这样的答案也是无缘offer的。
思路2:【只对K部分排序,冒泡或选择】
可以采用数据池的思想,选择其中前K个数作为数据池,后面的N-K个数与这K个数进行比较,若小于其中的任何一个数,则进行替换。这种思路的算法复杂度是O(N*K),当答出这种算法时,似乎离offer很近了。
有没有算法复杂度更低的方法呢?
从思路2可以想到,剩余的N-K个数与前面K个数比较的时候,是顺序比较的,算法复杂度是K。怎么在这方面做文章呢? 采用的数据结构是堆。
思路3:【K部分堆排序】
大根堆维护一个大小为K的数组,目前该大根堆中的元素是排名前K的数,其中根是最大的数。此后,每次从原数组中取一个元素与根进行比较,如小于根的元素,则将根元素替换并进行堆调整(下沉),即保证大根堆中的元素仍然是排名前K的数,且根元素仍然最大;否则不予处理,取下一个数组元素继续该过程。该算法的时间复杂度是O(N*logK),一般来说企业中都采用该策略处理topK问题,因为该算法不需要一次将原数组中的内容全部加载到内存中,而这正是海量数据处理必然会面临的一个关卡。如果能写出代码,offer基本搞定。
class Solution: def __init__(self): self.n = 0 def heap_sort(self,arr): self.n = len(arr) self.buildHeap(arr) return arr def buildHeap(self,arr): for i in range(self.n//2-1,-1,-1): self.adjustHeap(arr,i) def adjustHeap(self,arr,i): maxIndex = i if i * 2 < self.n and arr[i*2] > arr[i]: maxIndex = i * 2 if i * 2 + 1 < self.n and arr[i*2 +1] > arr[i]: maxIndex = i * 2 + 1 if maxIndex != i: arr[i] , arr[maxIndex] = arr[maxIndex] , arr[i] self.adjustHeap(arr,maxIndex) def GetLeastNumbers_Solution(self, tinput, k): # write code here if not tinput or k <= 0 or k > len(tinput): return [] if len(tinput) == k: return sorted(tinput) arr = self.heap_sort(tinput[:k]) for i in range(k,len(tinput)): if tinput[i] < arr[0]: arr[0],tinput[i] = tinput[i],arr[0] self.heap_sort(arr) return sorted(arr)
还有没有更简单的算法呢?答案是肯定的。
思路4:【不排序---快排】
利用快速排序的分划函数找到分划位置K,则其前面的内容即为所求。该算法是一种非常有效的处理方式,时间复杂度是O(N)(证明可以参考算法导论书籍)。对于能一次加载到内存中的数组,该策略非常优秀。如果能完整写出代码,那么相信面试官会对你刮目相看的。
优点:
每次经过划分,如果中间值等于 K ,那么其左边的数就是 Top K 的数据;
当然,如果不等于,只要递归处理左边或者右边的数即可
该方法的时间复杂度是 O(n) ,简单分析就是第一次划分时遍历数组需要花费 n,而往后每一次都折半(当然不是准确地折半),粗略地计算就是 n + n/2 + n/4 +... < 2n,因此显然时间复杂度是 O(n)
对比第一个方法显然快了不少,随着数据量的增大,两个方法的时间差距会越来越大
缺点
虽然时间复杂度是 O(n) ,但是缺点也很明显,最主要的就是内存问题,在海量数据的情况下,我们很有可能没办法一次性将数据全部加载入内存,这个时候这个方法就无法完成使命了
还有一点就是这种思路需要我们修改输入的数组,这也是值得考虑的一点
下面,给出思路4的Python代码:
def partition(L, left, right): """ 将L[left:right]进行一次快速排序的partition,返回分割点 :param L: 数据List :param left: 排序起始位置 :param right: 排序终止位置 :return: 分割点 """ if left < right: print left key = L[left] low = left high = right while low < high: while low < high and L[high] >= key: high = high - 1 L[low] = L[high] while low < high and L[low] <= key: low = low + 1 L[high] = L[low] L[low] = key return low def topK(L, K): """ 求L中的前K个最小值 :param L: 数据List :param K: 最小值的数目 """ if len(L) < K: pass low = 0 high = len(L) - 1 j = partition(L, low, high) while j != K: # 划分位置不是K则继续处理 if K > j: #k在分划点后面部分 low = j + 1 else: high = j # K在分划点前面部分 j = partition(L, low, high)
解决思路4缺点. 利用分布式思想处理海量数据
面对海量数据,我们就可以放分布式的方向去思考了
我们可以将数据分散在多台机器中,然后每台机器并行计算各自的 TopK 数据,最后汇总,再计算得到最终的 TopK 数据
这种数据分片的分布式思想在面试中非常值得一提,在实际项目中也十分常见
扩展问题:
1.如果需要找出N个数中最大的K个不同的浮点数呢?比如,含有10个浮点数的数组(1.5,1.5,2.5,3.5,3.5,5,0,- 1.5,3.5)中最大的3个不同的浮点数是(5,3.5,2.5)。
解答:四种思路都可以。
2. 如果是找第k到第m(0<k<=m<=n)大的数呢?
解答:可以用小根堆来先求出m个最大的,然后从中输出k到m个。
3. 在搜索引擎中,网络上的每个网页都有“权威性”权重,如page rank。如果我们需要寻找权重最大的K个网页,而网页的权重会不断地更新,那么算法要如何变动以达到快速更新(incremental update)并及时返回权重最大的K个网页?
解答:(解法三)用堆排序当每一个网页权重更新的时候,更新堆。
举一反三:查找最小的K个元素
解答:最直观的方法是用快速排序或堆排序先排好,在取前K小的数据。最好的办法是利用解法四和解法三的原理进行查找。

