Alias采样算法
一、离散分布
离散分布:给你一个概率分布,是离散的,比如[1/2, 1/3, 1/12, 1/12],代表某个变量属于事件A的概率为1/2, 属于事件B的概率为1/3,属于事件C的概率为1/12,属于事件D的概率为1/12。
离散分布的随机变量的取样问题:
一个随机事件包含四种情况,每种情况发生的概率分别为: 1/2, 1/3, 1/12, 1/12,问怎么用产生符合这个概率的采样方法。
二、时间复杂度为o(N)的采样算法
首先将其概率分布按其概率对应到线段上,像下图这样:

接着产生0~1之间的一个随机数,然后看起对应到线段的的哪一段,就产生一个采样事件。比如落在0~ 1/2之间就是事件A,落在1/2~5/6之间就是事件B,落在5/6~11/12之间就是事件C,落在11/12~1之间就是事件D。
构建线段的时间复杂度为o(N),
如果顺序查找线段的话,查找时间复杂度为O(N),
如果二分查找的话,查找的时间复杂度为O(logN)。
三、时间复杂度O(1)的采样算法---Alias
(1)alias分为两步
- 做表
- 根据表采样
(2)做表
将概率分布的每个概率乘上N,画出柱状图。N为事件数量。

其总面积为N,可以看出某些位置面积大于1某些位置的面积小于1,
将面积大于1的事件多出的面积补充到面积小于1对应的事件中,以确保每一个小方格的面积为1,同时,保证每一方格至多存储两个事件,这样我们就能看到一个1*N的矩形啦。

表里面有两个数组,一个数组存储的是事件i占第i列矩形的面积的比例,即![]()
另一个数组存储第i列中不是事件i的另一个事件的编号,即![]() 。
。
做表的时间复杂度是o(N)。
(3)采样
产生两个随机数,
第一个产生一个1~N 之间的整数 i,决定落在哪一列。
第二个产生一个0~1之间的随机数,判断其与Prab[i]大小,
如果小于Prab[i],则采样 i,(表示若其小于事件i占第i列矩形的面积的比例,则表示接受事件i)
如果大于Prab[i],则采样Alias[i](否则,接收第i列中不是事件i的另一个事件。)
【这种方式采样的时间复杂度为 o(1) ,且对应事件i的概率,完全对应原来的概率分布。】
计算:选择第一列的概率为1/4,则选择第一列的蓝色部分的概率为1/4*2/3 = 1/6,蓝色部分还有第三、第四列,则蓝色(事件A)的总概率为1/4 * 2/3 * 3 = 1/2。【第一次产生随机数的概率为1/4,第二次产生随机数选择蓝色部分的概率为1/4 *(2/3*3) = 1/2】。--------对应原来的概率分布。
四、代码
1、制作表:(create_alias_table函数,O(N))
(1)概率分布 area_ratio 的每个概率乘上N
(2)small,large分别存放小于1和大于1的事件下标。
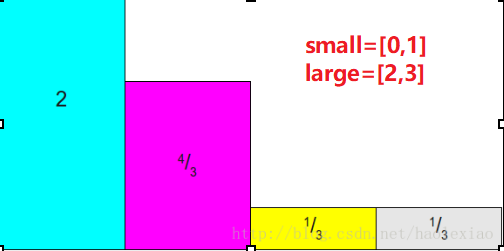
(3)每次从small,large中各取一个,将大的补充到小的之中,小的出队列,再看大的减去补给之后,如果大于1,继续放入large中,如果等于1,则也出去,如果小于1则放入small中。

(4)获取accept、alias
accept存放第i列对应的事件i矩形的面积百分比;
alias存放第i列不是事件i的另外一个事件的标号;
上例中accept=[2/3,1,1/3,1/3],alias=[2,0,1,1],这里alias[1]的0是默认值,也可默认置为-1避免和事件0冲突;
2、采样:(alias_sample函数,O(1))
随机采样1~N 之间的整数i,决定落在哪一列。
随机采样0~1之间的一个概率值,
如果小于accept[i],则采样i,
如果大于accept[i],则采样alias[i];
import numpy as np def create_alias_table(area_ratio): """ area_ratio[i]代表事件i出现的概率 :param area_ratio: sum(area_ratio)=1 :return: accept,alias """ N = len(area_ratio) accept, alias = [0] * N, [0] * N small, large = [], []
###------(1)概率 * N ----- area_ratio_ = np.array(area_ratio) * N
###------(2)获取small 、large ----- for i, prob in enumerate(area_ratio_): if prob < 1.0: small.append(i) else: large.append(i)
###------(3)修改柱状图 ----- (4)获取accept和alias ----- while small and large: small_idx, large_idx = small.pop(), large.pop() accept[small_idx] = area_ratio_[small_idx] alias[small_idx] = large_idx area_ratio_[large_idx] = area_ratio_[large_idx] - \ (1 - area_ratio_[small_idx]) if area_ratio_[large_idx] < 1.0: small.append(large_idx) else: large.append(large_idx)
while large: large_idx = large.pop() accept[large_idx] = 1 while small: small_idx = small.pop() accept[small_idx] = 1 return accept, alias def alias_sample(accept, alias): """ :param accept: :param alias: :return: sample index """ N = len(accept) i = int(np.random.random()*N) r = np.random.random() if r < accept[i]: return i else: return alias[i]
参考文献:

