python学习（32）---networkx

一、networkx介绍

NetworkX提供图形（或网络）的数据结构以及图形算法，生成器和绘图工具。

函数，方法和变量名是lower_case_underscore（小写，下划线表示单词之间的空格）。

 

二、基础

1、导入模块

import networkx as nx

2、图/网络

图的类型

• Graph：无多重边无向图。忽略两个节点之间的多个边，允许节点自身成环。
• DiGraph：无多重边有向图
• MultiGraph：有多重边无向图，允许在成对的节点之间存在多个无向边。
• MultiDIGraph：有多重边有向图

所有图类均允许任何可哈希对象作为节点。可哈希对象包括字符串，元组，整数等。如权重和标签之类的任意边属性都可以与边相关联。

   G = nx.Graph()#创建空的网络图
   G = nx.DiGraph()
   G = nx.MultiGraph()
   G = nx.MultiDiGraph()

图的创建：（三种方式）

1. 图生成器，如例如binomial_graph和powerlaw_graph
2. 从文本源中加载数据，如nx.read_adjlist
3. 自主创建空图并添加点和边

 

3、节点和边

• 节点：整数 / 字符串 / 描述节点的数据结构
• 边：关键字/值对【可使用除'weight'以外的任何关键字来命名属性，可通过此关键字查询边】

（1）添加：

#添加点
G.add_node('a')#添加点a
G.add_node(1,1)#用坐标来添加点
G.add_nodes_from([2, 3])  #添加一列表的节点

##或者 添加一系列迭代器
H = nx.path_graph(10)
G.add_nodes_from(H)

G.add_node(math.cos) # any hashable can be a node

#添加边

G.add_edge('x','y')#添加边,起点为x，终点为y，默认边值为1
G.add_edge(1,3,weight=0.9) #添加边,起点为1，终点为2，权重值为0.9

G.add_edge('y','x',function=math.cos) #Edge attributes can be anything

G.add_edges_from([(1, 2), (1, 3)])

G.add_weight_edges_from([('x','y',1.0)])#第三个输入量为权值
#也可以
list = [[('a','b',5.0),('b','c',3.0),('a','c',1.0)]
G.add_weight_edges_from([(list)])

（2） 删除：

  g.remove_node()

  g.remove_nodes_from()

  g.remove_edge()

  g.remove_edges_from()

  g.remove_edge( 1,2);   #删除node1和node2之间的edge，自此node1和node2不再为相邻的node

  g.remove_edges_from(edges_list)

##删除所有的点和边
G.clear()

##删除边的属性

del g[1][2][‘name‘]

（3）查看：

G.number_of_nodes()
#8，节点数量
G.number_of_edges()
#3，边数量

 #获取一个Graph对象中的node数组或者edge数组

  g.nodes();

  g.edges();

 

 #查看边的数据

g[1][2]  #方式1，查看边（1,2）的属性，如可以有权重，关系，颜色等，输出结果为{'weight':1}
g.get_edge_data(1,2)  #方式2，输出结果为{‘weight‘: 0.125, ‘relationship‘: ‘renew‘, ‘color‘: ‘blue‘}

# 查看邻居
g.neighbors(1);   #获取与node为1相邻的node是节点，是一个迭代器

#查看边是否存在
g.has_edge(1,2)

 

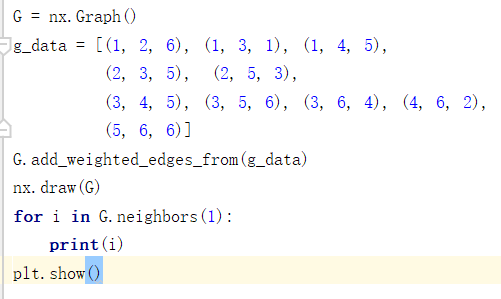
 输出结果：

2
3
4

（4）更新：

通过边来更新边的属性，由两种方式，一种是使用update函数，一种是通过属性赋值来实现：

g[1][2][‘weight‘] = 4.7
g.edge[1][2][‘weight‘] = 4
g[1][2].update({"weight": 4.7})
g.edges[1, 2].update({"weight": 4.7})   

 

4、图形的显示

需要导入matplotlib
import matplotlib.pyplot as plt

nx.draw(G)
#nx.draw_networkx(G)

plt.show()

#若想让图形更精美
nx.draw(G,pos = nx.random_layout(G)，node_color = 'b',edge_color = 'r',with_labels = True，font_size =18,node_size =20)

pos 指的是布局 主要有spring_layout , random_layout,circle_layout,shell_layout。node_color指节点颜色，有rbykw ,同理edge_color.
with_labels指节点是否显示名字,size表示大小，font_color表示字的颜色。

5、基本操作

import networkx as nx

oo = float('inf')

# 创建无向图
G = nx.Graph()
G.add_node(1) # 添加节点１
G.add_edge(2,3) #　添加节点２，３并链接２３节点
print(G.nodes, G.edges, G.number_of_nodes(), G.number_of_edges())

# 创建有向图
G = nx.DiGraph() 
G.add_edge(2, 3)
G.add_edge(3, 2)
G.to_undirected()  # 转换成无向图
print(G.edges)

# 加权图
G = nx.DiGraph()
G.add_weighted_edges_from([(0,1,3.0), (1,2,7.5)]) # 给０１边加权３，　１２边加权７．５
print(G.get_edge_data(1,2))  # 获得１２边的属性

G.add_weighted_edges_from([(2,3,5)], weight='color')
print(G.edges.data())

G.node[1]['size'] = 10
print(G.nodes.data())


import matplotlib.pyplot as plt

g_data = [(1, 2, 6), (1, 3, 1), (1, 4, 5),
          (2, 3, 5),  (2, 5, 3),
          (3, 4, 5), (3, 5, 6), (3, 6, 4), (4, 6, 2),
          (5, 6, 6)]

# 最小生成树
g = nx.Graph()
g.add_weighted_edges_from(g_data)
tree = nx.minimum_spanning_tree(g, algorithm='prim')
print(tree.edges(data=True))

# 最短路径
G = nx.path_graph(5)  # 0-1-2-3-4链
print(nx.dijkstra_path(G, 0, 4))

# 所有节点之间的最短路径
G = nx.Graph()
G.add_weighted_edges_from(g_data)
gen = nx.all_pairs_shortest_path(G)
print(dict(gen))

# 各点之间可达性
G = nx.Graph()
G.add_weighted_edges_from(g_data)
print(nx.communicability(G))

# 获得图中非连通点的列表
G = nx.Graph()
G.add_edge(1,2)
G.add_node(3)
print(list(nx.isolates(G)))

# 遍历
G = nx.Graph()
G.add_weighted_edges_from(g_data)
d_gen = nx.dfs_edges(G,1)  #  按边深度搜索, 1为起点
b_gen = nx.bfs_edges(G,1)
print(list(d_gen), list(b_gen))
print(nx.dfs_tree(G,1).nodes())  # 按点深搜


from networkx.algorithms.flow import shortest_augmenting_path
import matplotlib.pyplot as plt

G = nx.DiGraph()
G.add_edge('x','a', capacity=3.0)
G.add_edge('x','b', capacity=1.0)
G.add_edge('a','c', capacity=3.0)
G.add_edge('b','c', capacity=5.0)
G.add_edge('b','d', capacity=4.0)
G.add_edge('d','e', capacity=2.0)
G.add_edge('c','y', capacity=2.0)
G.add_edge('e','y', capacity=3.0)

# 将参数画到图上
pos = nx.spring_layout(G)
capacity = nx.get_edge_attributes(G, 'capacity')
# nx.draw_networkx_nodes(G, pos)
# nx.draw_networkx_edges(G, pos)
# nx.draw_networkx_labels(G, pos)
# nx.draw_networkx_edge_labels(G,pos,capacity)

# 最大流
flow_value, flow_dict = nx.maximum_flow(G,'x', 'y', flow_func=shortest_augmenting_path)
print(flow_value, flow_dict)
# plt.show()


# 最小成本流
G = nx.DiGraph()
G.add_node('a', demand = -5)
G.add_node('d', demand = 5)
G.add_edge('a', 'b', weight = 3, capacity = 4)
G.add_edge('a', 'c', weight = 6, capacity = 10)
G.add_edge('b', 'd', weight = 1, capacity = 9)
G.add_edge('c', 'd', weight = 2, capacity = 5)
flow_cost, flow_dict = nx.capacity_scaling(G)
print(flow_cost, flow_dict)

# 欧拉回路  一个无向图G,一条路径经过图G的每一条边,且仅经过一次,这条路径称为欧拉路径．如果起点和终点同一点，则为欧拉回路
# 无向图：每个顶点的度数都是偶数则存在欧拉回路
# 有向图：每个顶点的入度都等于出度则存在欧拉回路
DG = nx.DiGraph({0: [3], 1: [2], 2: [3], 3: [0, 1]})
G = nx.Graph({0: [1,2], 1: [0,2], 2: [0,1,3,4], 3: [2,4], 4:[2,3]})
print(nx.is_eulerian(DG))
print(nx.is_eulerian(G))
print(list(nx.eulerian_circuit(DG)))
print(list(nx.eulerian_circuit(G)))

# 最小点割集
node_cut = nx.minimum_node_cut(G, flow_func=shortest_augmenting_path)
print(node_cut)

# 对于带权无向图边切割，得到最小切割权之和，以及两个分离区域
G = nx.Graph()
G.add_edge('x','a', weight=3)
G.add_edge('x','b', weight=1)
G.add_edge('a','c', weight=3)
G.add_edge('b','c', weight=5)
G.add_edge('b','d', weight=4)
G.add_edge('d','e', weight=2)
G.add_edge('c','y', weight=2)
G.add_edge('e','y', weight=3)

cut_value, partition = nx.stoer_wagner(G)
print(cut_value, partition)

# 最大权重匹配　匈牙利、KM算法
G = nx.Graph()
G.add_weighted_edges_from([('A', 'a', 3), ('A', 'c', 4), ('B', 'a', 2), ('B', 'b', 1), ('B', 'c', 3), ('C', 'c', 5)])
print(nx.max_weight_matching(G))

# 拓扑排序
G = nx.DiGraph()
G.add_edge('x','a', weight=3)
G.add_edge('a','c', weight=3)
G.add_edge('b','c', weight=5)
G.add_edge('b','d', weight=4)
G.add_edge('d','e', weight=2)
G.add_edge('c','y', weight=2)
G.add_edge('e','y', weight=3)
print(list(nx.topological_sort(G)))

# 最小成本最大流
G = nx.DiGraph()
G.add_edge('a', 'b', weight = 3, capacity = 4)
G.add_edge('a', 'c', weight = 6, capacity = 10)
G.add_edge('b', 'd', weight = 1, capacity = 9)
G.add_edge('c', 'd', weight = 2, capacity = 5)
print(nx.max_flow_min_cost(G, 'a', 'd'))


#复杂网络生成
# ER随机图   # 随机生成20个节点，节点间的连接概率都是0.2
# ER = nx.random_graphs.erdos_renyi_graph(20, 0.2)
# pos = nx.shell_layout(ER)
# nx.draw(ER, pos, with_labels=False,edge_color='b', alpha=0.3, node_size=30)
# plt.show()

# WS小世界网络  生成一个含有n个节点、每个节点有k个邻居、以概率p随机化重连边的WS小世界网络。
WS = nx.random_graphs.watts_strogatz_graph(20, 4, 0.3)
pos = nx.circular_layout(WS)
nx.draw(WS, pos, with_labels=False, node_size=30, edge_color='b', alpha=0.3)
plt.show()


# BA无标度网络 生成一个含有n个节点、每次加入m条边的BA无标度网络
# BA = nx.random_graphs.barabasi_albert_graph(10,2)
# pos = nx.spring_layout(BA)
# nx.draw(BA, pos, with_labels=False, node_size=30, edge_color='b', alpha=0.3)
# plt.show()

# 扩展ＢＡ无标度网络  节点数，添加新边数，两点间添加边的概率，边重连的概率
# ExBA = nx.random_graphs.extended_barabasi_albert_graph(200, 4, 0.4, 0.2)
# pos = nx.spring_layout(ExBA)
# nx.draw(ExBA, pos, with_labels=False, node_size=30, edge_color='b', alpha=0.3)
# plt.show()

 

参考文献：

networkx整理

Tutorial

Python3画图系列——NetworkX初探（案例）

Python包 - networkx