图的BFS
目录:
https://blog.csdn.net/weixin_40953222/article/details/80544928
一、算法的基本思路
广度优先搜索类似于树的层次遍历过程。
它需要借助一个队列来实现。如图2-1-1所示,要想遍历从v0到v6的每一个顶点,我们可以设v0为第一层,v1、v2、v3为第二层,v4、v5为第三层,v6为第四层,再逐个遍历每一层的每个顶点。
具体过程如下:
1.准备工作:
创建一个visited数组,用来记录已被访问过的顶点;
创建一个队列,用来存放每一层的顶点;
初始化图G。
2.从图中的v0开始访问,将的visited[v0]数组的值设置为true,同时将v0入队。
3.只要队列不空,则重复如下操作:
(1)队头顶点u出队。
(2)依次检查u的所有邻接顶点w,若visited[w]的值为false,则访问w,并将visited[w]置为true,同时将w入队。
二、过程:
白色表示未被访问,灰色表示即将访问,黑色表示已访问。
visited数组:0表示未访问,1表示以访问。
队列:队头出元素,队尾进元素。
1.初始时全部顶点均未被访问,visited数组初始化为0,队列中没有元素。
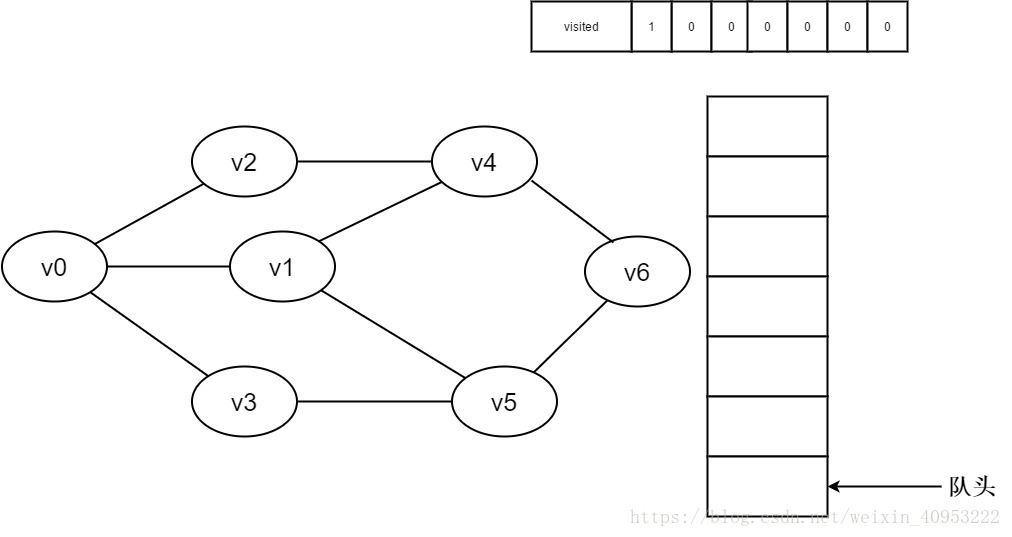
2.即将访问顶点v0。
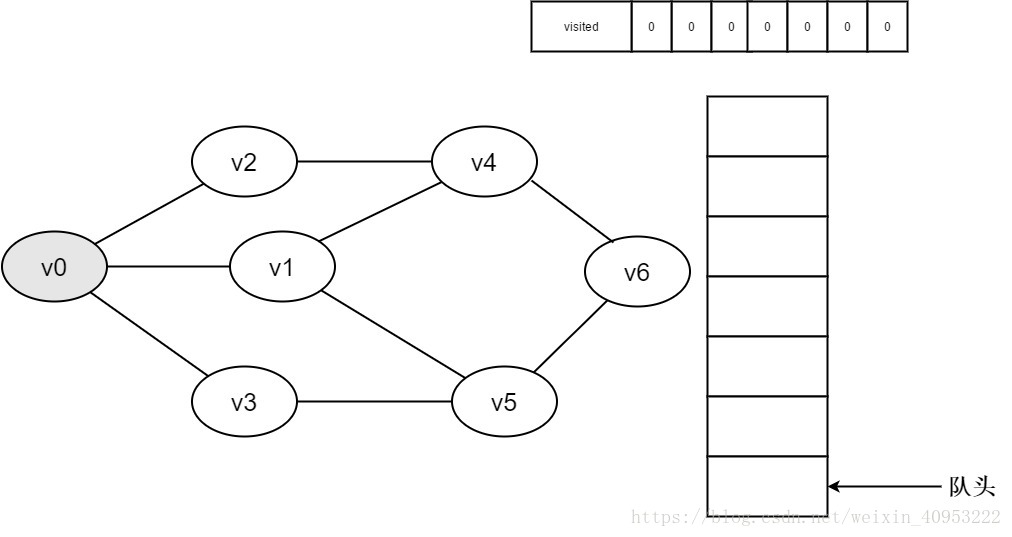
3.访问顶点v0,并置visited[0]的值为1,同时将v0入队。

4.将v0出队,访问v0的邻接点v2。判断visited[2],因为visited[2]的值为0,访问v2。

5.将visited[2]置为1,并将v2入队。

6.访问v0邻接点v1。判断visited[1],因为visited[1]的值为0,访问v1。
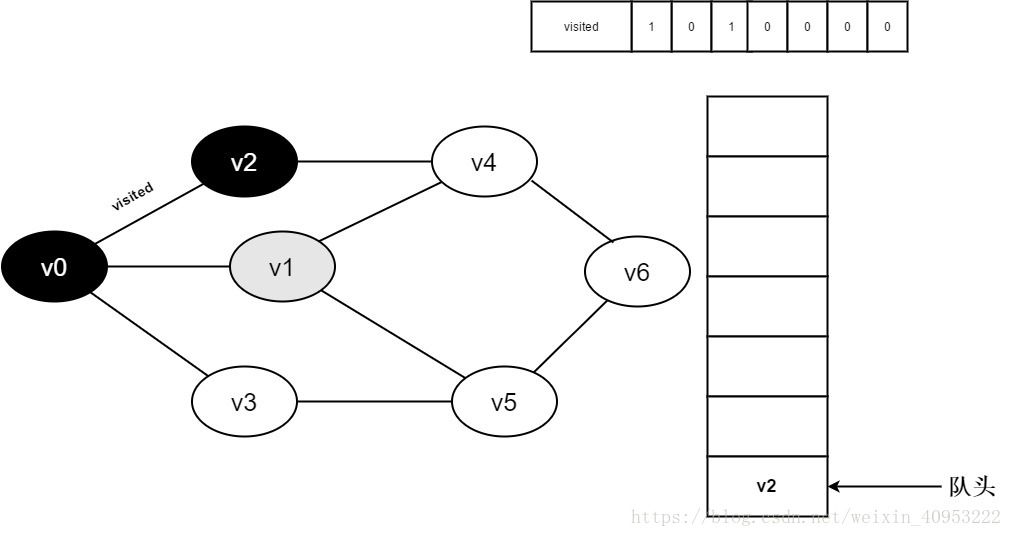
7.将visited[1]置为0,并将v1入队。
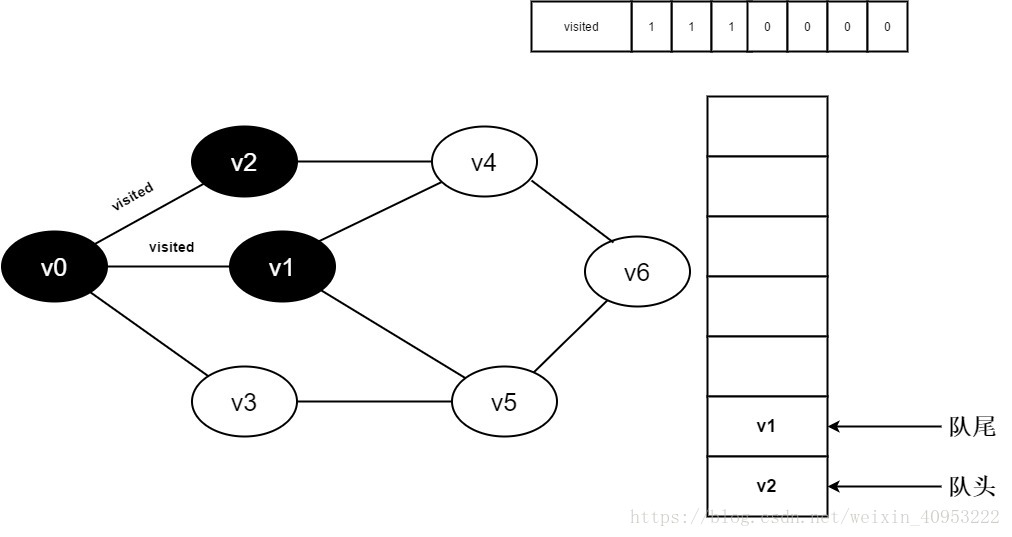
8.判断visited[3],因为它的值为0,访问v3。将visited[3]置为0,并将v3入队。

9.v0的全部邻接点均已被访问完毕。将队头元素v2出队,开始访问v2的所有邻接点。
开始访问v2邻接点v0,判断visited[0],因为其值为1,不进行访问。
继续访问v2邻接点v4,判断visited[4],因为其值为0,访问v4,如下图:
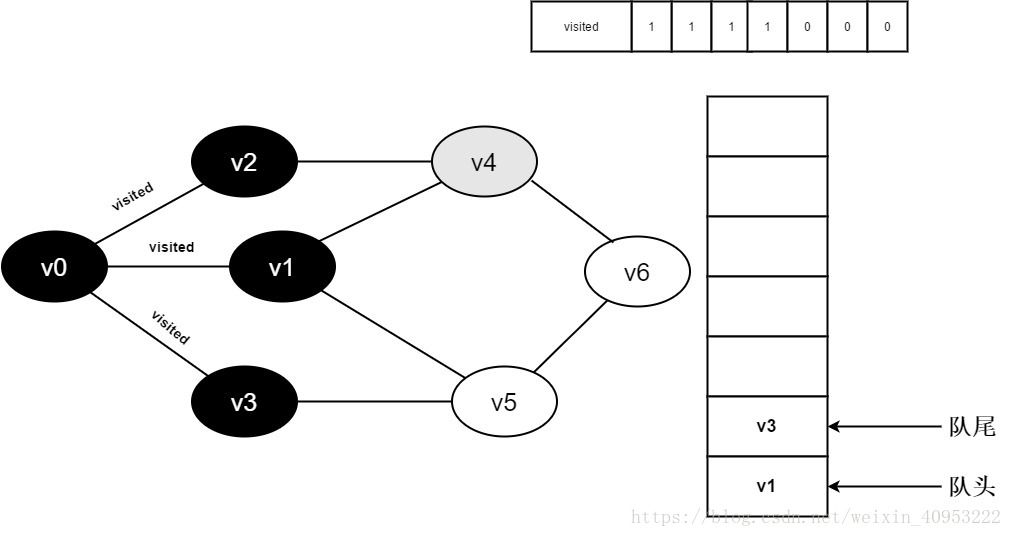
10.将visited[4]置为1,并将v4入队。

11.v2的全部邻接点均已被访问完毕。
将队头元素v1出队,开始访问v1的所有邻接点。开始访问v1邻接点v0,因为visited[0]值为1,不进行访问。
继续访问v1邻接点v4,因为visited[4]的值为1,不进行访问。
继续访问v1邻接点v5,因为visited[5]值为0,访问v5,如下图:

12.将visited[5]置为1,并将v5入队。
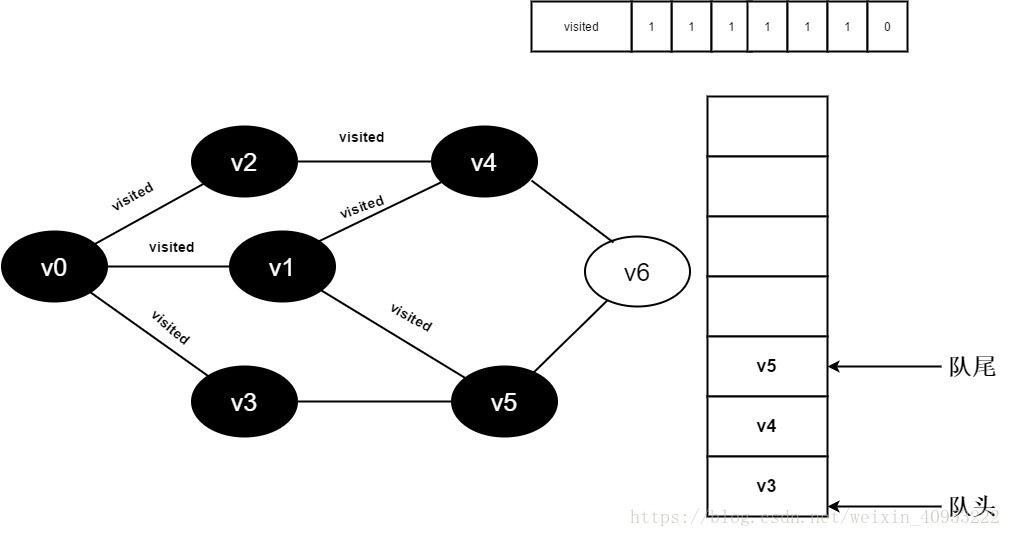
13.v1的全部邻接点均已被访问完毕,将队头元素v3出队,开始访问v3的所有邻接点。
开始访问v3邻接点v0,因为visited[0]值为1,不进行访问。
继续访问v3邻接点v5,因为visited[5]值为1,不进行访问。
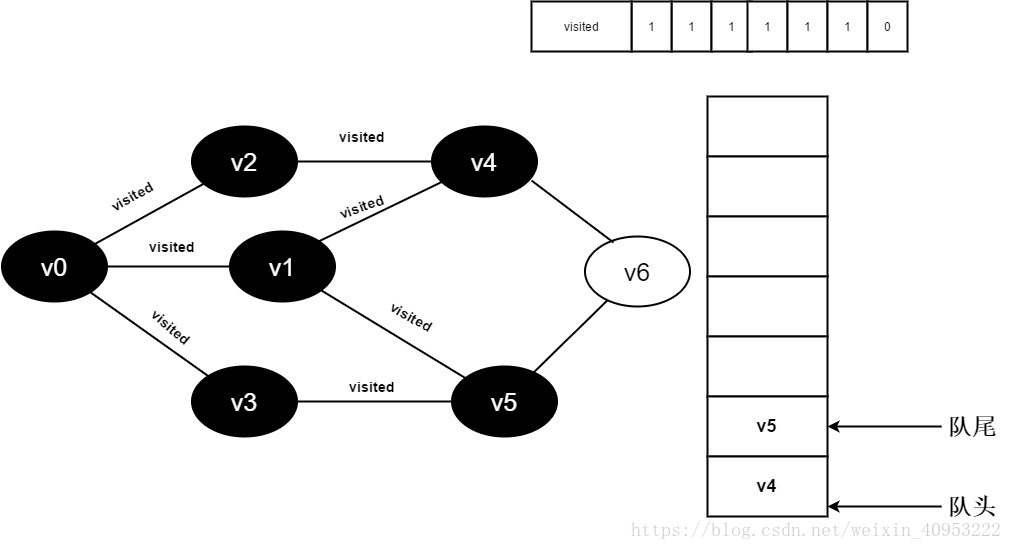
14.v3的全部邻接点均已被访问完毕,将队头元素v4出队,开始访问v4的所有邻接点。
开始访问v4的邻接点v2,因为visited[2]的值为1,不进行访问。
继续访问v4的邻接点v6,因为visited[6]的值为0,访问v6,如下图:
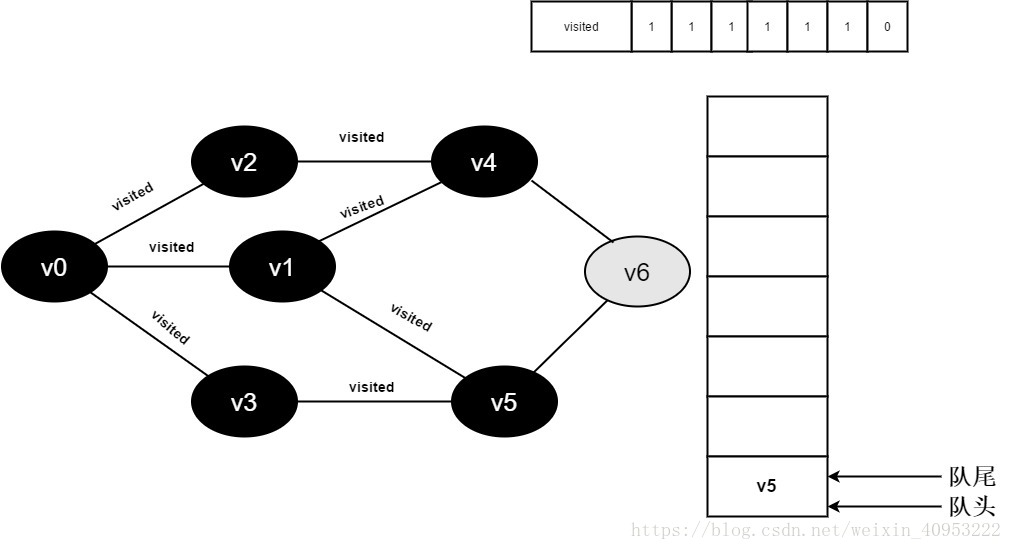
15.将visited[6]值为1,并将v6入队。
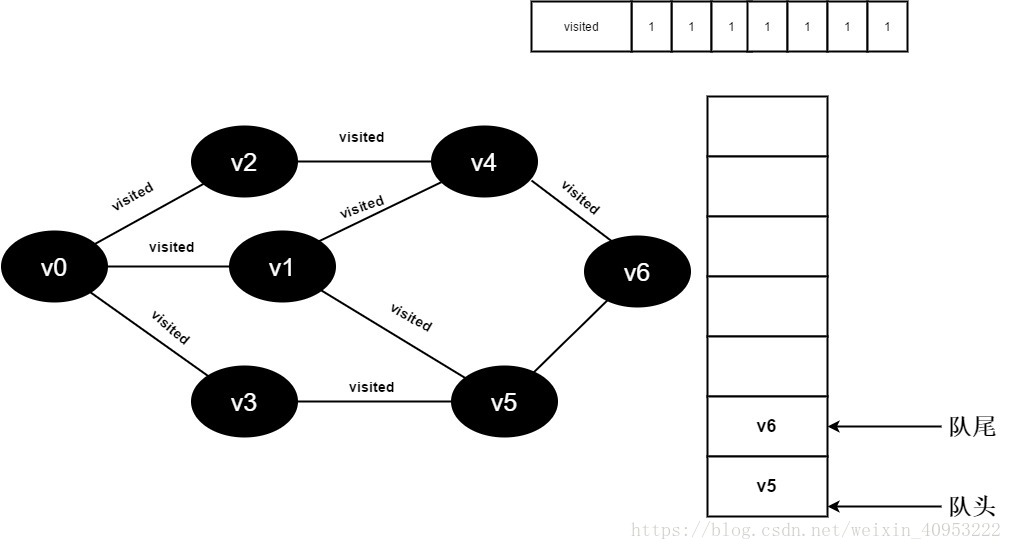
16.v4的全部邻接点均已被访问完毕,将队头元素v5出队,开始访问v5的所有邻接点。
开始访问v5邻接点v3,因为visited[3]的值为1,不进行访问。
继续访问v5邻接点v6,因为visited[6]的值为1,不进行访问。
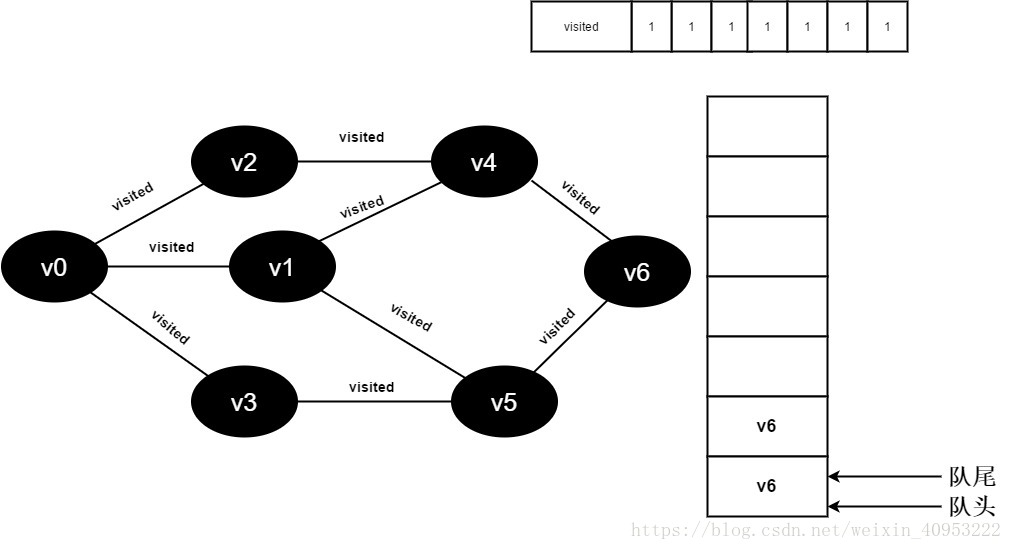
17.v5的全部邻接点均已被访问完毕,将队头元素v6出队,开始访问v6的所有邻接点。
开始访问v6邻接点v4,因为visited[4]的值为1,不进行访问。
继续访问v6邻接点v5,因为visited[5]的值文1,不进行访问。
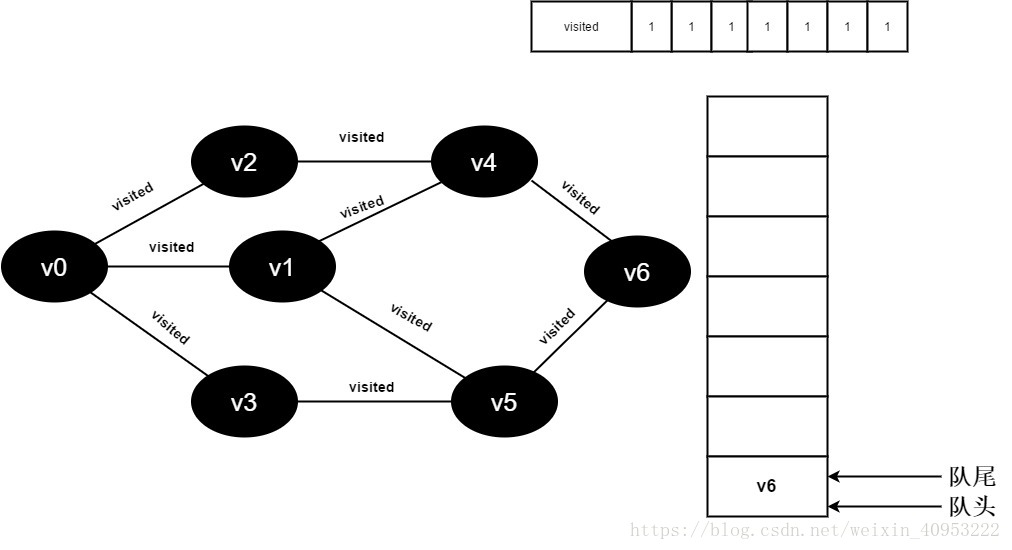
18.队列为空,退出循环,全部顶点均访问完毕。
题目:785判断二分图
给定一个无向图graph,当这个图为二分图时返回true。
如果我们能将一个图的节点集合分割成两个独立的子集A和B,并使图中的每一条边的两个节点一个来自A集合,一个来自B集合,我们就将这个图称为二分图。
graph将会以邻接表方式给出,graph[i]表示图中与节点i相连的所有节点。每个节点都是一个在0到graph.length-1之间的整数。这图中没有自环和平行边: graph[i] 中不存在i,并且graph[i]中没有重复的值。
示例 1:
输入: [[1,3], [0,2], [1,3], [0,2]]
输出: true
解释:
无向图如下:
0----1
| |
| |
3----2
我们可以将节点分成两组: {0, 2} 和 {1, 3}。
示例 2:
输入: [[1,2,3], [0,2], [0,1,3], [0,2]]
输出: false
解释:
无向图如下:
0----1
| \ |
| \ |
3----2
我们不能将节点分割成两个独立的子集。
注意:
graph的长度范围为[1, 100]。graph[i]中的元素的范围为[0, graph.length - 1]。graph[i]不会包含i或者有重复的值。- 图是无向的: 如果
j在graph[i]里边, 那么i也会在graph[j]里边。
思路:
分析: 用染色法,即从其中一个顶点开始,将跟它邻接的点染成与其不同的颜色,如果邻接的点有相同颜色的,则说明不是二分图
代码:
def bfs(s,graph,color,queue): color[s] = 1 queue.append(s) while queue: u = queue.pop() print(u) for v in graph[u]: if color[v] == 0: queue.append(v) color[v] = 0 - color[u] else: if color[v] == color[u]: return False return True def isBipartite(graph): if not graph: return False n = len(graph) color = [0] * n queue = [] for i in range(n): if color[i] == 0 and not bfs(i,graph,color,queue): return False return True graph = [[1,2,3],[0,2],[0,1,3],[0,2]] isBipartite(graph)

