算法68------数组和矩阵问题
目录:
- 转圈打印矩阵
- 将正方形矩阵顺时针转动90度
- “之”字形打印矩阵
- 找到无序数组中最小的k个数
- 需要排序的最短子数组长度【找到比当前最小值左边大的数和比最大值右边大的数的索引】
- 在数组中找到出现次数大于N/K的数【删除不同的数】
- 在行列都排好序的矩阵中找数
- 最长的可整合子数组的长度
- 不重复打印排序数组中相加和为给定值的所有二元组和三元组【左右变量遍历】
- 不重复打印排序数组中相加和为给定值的N元祖【递归】
- 未排序正整数数组中累加和等于给定值的最长子数组长度【左右变量遍历】
- 未排序数组中累加和为给定值的最长子数组系列问题【arr[i……j】=s[j]-s[i],采用字典存储和s】
- 未排序数组中累加和小于或等于给定值的最长子数组长度【列表存s,二分法查找列表】
- 计算数组的小和
- 自然数数组的排序
- 奇数下标都是奇数或偶数下标都是偶数【even、odd变量变量】
- 奇数在前,偶数在后,且原本位置不变,即稳定的。【插入】
- 子数组的最大累加和问题【设置当前和变量,小于0置0】
- 子矩阵的最大累加和问题
- 在数组中找到一个局部最小的位置
- 数组中三个数的最大累乘积【几个变量】
- 数组中子数组的最大累乘积 【动态规划】
- 打印N个数组整体最大的Top K【堆排序】
- 边界都是1的最大正方形大小【遍历+动态规划】
- 不包含本位置值的累乘数组【左右额外空间遍历】
- 数组的partition调整【快排思想】
- 求最短通路值【宽度优先】
- 数组中未出现的最小正整数【左右变量遍历】
- 数组排序之后相邻数的最大差值【桶排序】
- 查找满足条件的二维数组最大值和次大值之和。【前面最大变量 + 后面最大变量】(RMQ)
- 数组中的逆序对【树状数组】
- RMQ算法【树状数组】
1、转圈打印矩阵

思路:
时间复杂度:O(mn)
空间复杂度:O(1)
1、设置左上角的坐标(lu1,lu2)和右下角的坐标(rd1,rd2),4个变量。按照题目打印
(第一次:lu1=0,lu2=0---rd1=3,rd2=3)

2、打印完一次,左上角坐标(lu1+=1,lu2+=1),右下角的坐标(rd1 -= 1,rd2 -= 1),直到左上角坐标在右下角坐标的右下方。
(第二次:lu1=1,lu2=1---rd1=2,rd2=2)
![]()
代码:
def printmatrix(lu1,lu2,rd1,rd2,res): if lu1 == rd1: for i in range(lu2,rd2+1): res.append(matrix[lu1][i]) elif lu2 == rd2: for i in range(lu1,rd1+1): res.append(matrix[i][lu2]) else: curl1 , curl2 = lu1 , lu2 while curl2 != rd2: res.append(matrix[lu1][curl2]) curl2 += 1 while curl1 != rd1: res.append(matrix[curl1][rd2]) curl1 += 1 while curl2 != lu2: res.append(matrix[rd1][curl2]) curl2 -= 1 while curl1 != lu1: res.append(matrix[curl1][lu2]) curl1 -= 1 def OrderPrint(matrix): lu1 , lu2 = 0 , 0 rd1 , rd2 = len(matrix)-1 , len(matrix[0])-1 res = [] while lu1 <= rd1 and lu2 <= rd2: printmatrix(lu1,lu2,rd1,rd2,res) lu1 += 1 lu2 += 1 rd1 -= 1 rd2 -= 1 matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]] OrderPrint(matrix)
思路2:
时间复杂度:O(mn)
空间复杂度:O(1)
将已经走过的地方置0,然后拐弯的时候判断一下(取模)是不是已经走过了,如果走过了就计算一下新的方向(
di, dj = dj, -di
):
def printMatraix(): r, i, j, di, dj = [], 0, 0, 0, 1 if matrix != []: for _ in range(len(matrix) * len(matrix[0])): r.append(matrix[i][j]) matrix[i][j] = 0 if matrix[(i + di) % len(matrix)][(j + dj) % len(matrix[0])] == 0: di, dj = dj, -di i += di j += dj return r
2、将正方形矩阵顺时针转动90度

思路:
和上一题一样
1、设置左上角的坐标(lu1,lu2)和右下角的坐标(rd1,rd2),4个变量。旋转着改变矩阵
2、打印完一次,左上角坐标(lu1+=1,lu2+=1),右下角的坐标(rd1 -= 1,rd2 -= 1),直到左上角坐标在右下角坐标的右下方。
代码:
def rotate(matrix,lu1,lu2,rd1,rd2): times = rd1 - lu1 temp = 0 for i in range(times): temp = matrix[lu1][lu2+i] matrix[lu1][lu2+i] = matrix[rd1-i][lu2] matrix[rd1-i][lu2] = matrix[rd1][rd2-i] matrix[rd1][rd2-i] = matrix[lu1+i][rd2] matrix[lu1+i][rd2] = temp def rorateEdge(matrix): if not matrix or len(matrix) == 0 or len(matrix[0]) == 0: return matrix lu1 , lu2 , rd1 , rd2 = 0 , 0 , len(matrix)-1 , len(matrix[0])-1 while lu1 <= rd1 and lu2 <= rd2: rotate(matrix,lu1,lu2,rd1,rd2) lu1 += 1 lu2 += 1 rd1 -= 1 rd2 -= 1 return matrix matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]] rorateEdge(matrix)
思路2:
水平翻转,再对角线翻转

时间复杂度O(n2)
空间复杂度O(1)
def rorateEdge(matrix): # 水平翻转 for i in range(len(matrix)//2): for j in range(len(matrix[0])): matrix[i][j] ,matrix[len(matrix) -i -1][j]= matrix[len(matrix) -i -1][j],matrix[i][j] # 对角线翻转 for i in range(len(matrix)): for j in range(i): matrix[i][j],matrix[j][i] = matrix[j][i],matrix[i][j] print(matrix) matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]] rorateEdge(matrix)
3、“之”字形打印矩阵

思路:

代码:
def printZMatrix(matrix): if len(matrix) == 0 or len(matrix[0])==0: return matrix ld1 , ld2 = 0 , 0 ru1 , ru2 = 0 , 0 res = [] end1 , end2 = len(matrix)-1 , len(matrix[0])-1 sign = False while ru1 <= end1: printlr(matrix,ld1,ld2,ru1,ru2,res,sign) ru1 += 1 if ru2 == end2 else 0 ru2 += 1 if ru2 != end2 else 0 ld2 += 1 if ld1 == end1 else 0 ld1 += 1 if ld1 != end1 else 0 sign = ~sign return res def printlr(matrix,ld1,ld2,ru1,ru2,res,sign): # sign = True if ru2 % 2 == 0 else False if sign: while ru1 <= ld1: res.append(matrix[ru1][ru2]) ru1 += 1 ru2 -= 1 else: while ld1 >= ru1: res.append(matrix[ld1][ld2]) ld1 -= 1 ld2 += 1 matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]] printZMatrix(matrix)
思路2:
对角线上的下标和是一样的,一共有 len(matrix) + len(matrix[0]) - 1 条对角线。
对角线和为偶数时,从下往上打印,
对角线为奇数时,从上往下打印。
def printZMatrix(matrix): if len(matrix) == 0 or len(matrix[0])==0: return matrix res = [] time = len(matrix) + len(matrix[0]) for n in range(time): for i in range(n+1): if n % 2==1: if i < len(matrix) and (n-i) < len(matrix[0]): res.append(matrix[i][n-i]) else: if i < len(matrix[0]) and (n-i) < len(matrix): res.append(matrix[n-i][i]) return res matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]] printZMatrix(matrix)
4、找到无序数组中最小的k个数
要求:要求时间复杂度为O(Nlogk)和O(N)
如果先排序再找到最小的K个数,时间复杂度为O(NlogN)
【一个采用栈的思路:时间最坏为O(NK)】
采用栈来存储当前K个最小的值,栈中数值升序排序。
若栈的大小<K 且当前元素比栈顶元素大,则往栈中加元素。
否则,若当前元素比栈顶元素小,则将当前元素加入栈中,调整栈中元素的大小顺序并保证栈的大小为K。
代码:
def sortarr(arr,k): if not arr or k >= len(arr): return arr stack ,temp = [] , [] for i in range(len(arr)): if not stack: stack.append(arr[i]) else: if len(stack) < k and arr[i] >= stack[-1]: stack.append(arr[i]) while stack and arr[i] < stack[-1]: temp.append(stack.pop()) if temp: stack.append(arr[i])
if (len(stack) + len(temp) <= k):
stack.extend(temp[::-1])
else: stack.extend(temp[1:][::-1]) temp = [] return stack arr = [1,3,7,9,4,6,3,1,2,5,0] k = 4 sortarr(arr,k)
O(Nlogk)的思路:建立K个元素最大堆【空间O(K)】
一直维护一个大小为k的大根堆,这个堆表示目前选出的k个最小的数。
接下来遍历整个数组,
遍历过程中看当前数是否比堆顶元素小,如果是的话,将堆顶元素替换成当前的数,然后从堆顶向下调整堆;
否则,不进行任何操作。遍历结束后,堆中的k个数就是答案。
代码:【python的heapq只能建立一个最小堆,所以要建立最大堆,需要将数字取反放入堆中,取出时再取反】
import heapq def KNumHeap(arr,k): if k <= 0 or k >= len(arr) or len(arr) == 0: return arr max_heap = [] for i in range(len(arr)): cur = -arr[i] if len(max_heap) < k: heapq.heappush(max_heap,cur) else:
#heappushpop函数可以将一个cur元素插入最大堆中,保持堆的大小不变,即若cur > 堆顶元素,则cur不插入,堆不变。否则,删除堆顶元素,cur插入堆中正确位置 heapq.heappushpop(max_heap,cur) return list(map(lambda x:-x,max_heap)) arr = [1, 9, 2, 4, 7, 6, 3] k = 3 KNumHeap(arr,k)
5、需要排序的最短子数组长度
给定一个无序数组arr,求出需要排序的最短子数组长度。
例如:arr = 【1,5,3,4,2,6,7】返回4,因为只有【5,3,4,2】需要排序。
思路:时间O(N),空间O(1)
从右往左遍历,找最小值,如果最小值左边有比其大的数,索引就到此处。
从左往右遍历, 找最大值,如果最大值右边有比其小的数,索引就到此处。
如以下,红圈2为从右往左遍历到的最小值,左边比其大的数为其左边绿框的5,3,8,4。【为何不是1,因为1,2已在最左边放好】,nominindex = 2
红圈9为从左往右遍历得到的最大值,右边比其小的数为4。maxindex = 10
结果巍峨10-2+1=9

代码:
def getMinLen(arr): if not arr or len(arr) < 2: return 0 minnum = arr[len(arr)-1] nominindex = -1 for i in range(len(arr)-2,-1,-1): if arr[i] > minnum: nominindex = i else: minnum = min(minnum,arr[i]) if nominindex == -1: return 0 maxnum = arr[0] nomaxindex = -1 for i in range(1,len(arr)): if arr[i]<maxnum: nomaxindex = i else: maxnum = max(maxnum,arr[i]) return nomaxindex - nominindex + 1 arr = [1,2,5,3,8,4,2,6,7,9,4] getMinLen(arr)
6、在数组中找到出现次数大于N/K的数

思路:找到出现最多的那个数且次数超过一半。方法是遍历过程中成对删除不同的数,一个数如果出现次数超过一半,剩下的数必是该数,否则可能是也可能不是。如:
【4,3,7,4,4,4,5】,设置一个cand和time变量。开始,
开始,cand = 4,time= 1,
遇到下一个数3,两者不同,time - 1 = 0
遇到下一个数7,因为time=0,所以cand重置为=7,time=1
遇到下一个数4,cand和4不同,所以time - 1 =0
遇到下一个数4,time = 0,cand重置为4,time= 1
遇到下一个数4,cand和4相同,time + 1 = 2
遇到下一个数5,cand和5不同,time - 1 = 1
故:剩下的数cand为4。
然后从头开始遍历,判断4是否出现超过一半【因为如果没超过一半也可能cand为4,如 [ 4,3,4,5]】
代码:
def printHalfMajor(arr): if arr == None or len(arr) == 0: print("No such number!") return False cand = 0 time = 0 for i in range(len(arr)): if time == 0: cand = arr[i] time += 1 elif cand == arr[i]: time += 1 else: time -= 1 time = 0 for i in range(len(arr)): if arr[i] == cand: time += 1 if time > len(arr)//2: return True else: return False arr=[4,3,4,3,4,6,5,4] printHalfMajor(arr)
进阶问题思路:一次删掉K个不同的数,多次删除,直到剩下的数种类不足K。若一个数出现次数超过N/K,该数最后一定会剩下。
一个map记录K个不同的数,一旦map大小==k-1,且下一个arr[i]不在map中,就可以开始删除map中K个不同值。
代码:
def printHalfMajor(arr,k): if arr == None or len(arr) <= k: print("No such number!") return False #重点:每次删除K种不同的值【采用字典存储K种不同的值】 map = {} for i in range(len(arr)): if arr[i] in map: map[arr[i]] += 1 else: if len(map) == k-1: for key in list(map): map[key] -= 1 if map[key] == 0: del map[key] else: map[arr[i]] = 1 #查询map剩余的数在原数组中的数量 time = 0 flag = False for key in map: for i in range(len(arr)): if arr[i] == key: time += 1 if time > len(arr)//k: flag = True print(key) time = 0 return flag arr=[4,3,4,3,4,6,5,4] K = 3 printHalfMajor(arr,K)
7、在行列都排好序的矩阵中找数


思路:

8、最长的可整合子数组的长度

思路:时间O(n3),空间O(n)

代码:
def longestSubArr(arr): if not arr: return 0 res = 0 for i in range(len(arr)): for j in range(i,len(arr)): if isValid(arr[i:j+1]): res = max(res,j - i + 1) return res def isValid(arr): sortArr = sorted(arr) for i in range(len(sortArr)-1): if sortArr[i] != sortArr[i+1] - 1: return False return True arr = [5,5,3,2,6,4,3] longestSubArr(arr)
思路:时间O(n2),时间是在验证阶段缩短的,采取的验证方法是无重复数且总个数=最大值-最小值+1。


代码:采用一个集合来判断是否有重复数。

9、不重复打印排序数组中相加和为给定值的所有二元组和三元组


二元组的思路:时间O(N)

代码:
def two(arr,k): if not arr or len(arr)<2: return None res = [] left = 0 right = len(arr) - 1 while left < right: if arr[left] + arr[right] == k: if left == 0 or left > 0 and arr[left] != arr[left-1]: print(arr[left],arr[right]) left += 1 right -= 1 elif arr[left] + arr[right] < k: left += 1 elif arr[left] + arr[right] > k: right -= 1 arr=[-8,-4,-3,0,1,2,4,5,8,9] k=10 two(arr,k)
三元组思路:时间O(N2)

代码:
def two(arr,f,l,r,k): while l < r: if arr[l] + arr[r] < k: l += 1 elif arr[l] + arr[r] > k: r -= 1 else: if l == f+1 or arr[l-1] != arr[l]: print(arr[f], ',' , arr[l] , ',' , arr[r]) l += 1 r -= 1 def three(arr,k): if not arr or len(arr) < 3: return False for i in range(len(arr)): if i == 0 or arr[i] != arr[i-1]: two(arr,i,i+1,len(arr)-1,k-arr[i]) arr = [-8,-4,-3,0,1,2,4,5,8,9] k = 10 three(arr,k)
10、找出数组中和为K的一组解【递归+动态规划】
考虑N个数的数组A中是否存在和为K的解,可以分为考虑(N-1个数中是否有和为K的解)或者(N-1个数中是否有和为K-A[N-1]的解(解包含A[N-1]的情况))。
也就是说,动态规划方程是:P[n][k]=P[n-1][k] || P[n-1][ k-arr[n-1] ];
另一种解法:https://www.tuicool.com/articles/eEfe2mf【采用栈】
#include<vector>
11、未排序正整数数组中累加和等于给定值的最长子数组长度
给定一个数组arr,该数组无序,但每个值为正数,再给定一个正数k。求arr的所有子数组中所有元素相加和为k的最长子数组长度。
例如,arr=【1,2,1,1,1】,k=3。
累加和为3的最长子数组为【1,1,1】,所以结果为3
思路:时间O(N),空间O(1)
设置两个指针变量left,right。遍历数组,直到 right < len(arr)。不用担心left,因为只要left>right,下一步right就会+1.初始状态,两者都为0。
变量lrsum记录,left到right的和。变量res记录结果,即=k的子数组最长长度。
- 若 lrsum == k:【left右移】
res = max(res,right - left +1)
lrsum -= arr[left]
left += 1
- 若 lrsum < k:【right右移】
right += 1
若right==len(arr):break
lrsum += arr【right】
- 若 lrsum > k:【left右移】
lrsum -= arr[left]
left += 1
代码:
def getMaxlen(arr,k): if not arr or len(arr)<1: return 0 left , right = 0 , 0 res , lrsum = 0 , arr[0] while right < len(arr): if lrsum == k: res = max(res,right - left + 1) lrsum -= arr[left] left += 1 elif lrsum < k: right += 1 if right == len(arr): break lrsum += arr[right] else: lrsum -= arr[left] left += 1 arr = [2,2,9,2] k = 4 getMaxlen(arr,k)
11、未排序数组中累加和为给定值的最长子数组系列问题
题目:
给定一个无序数组arr,其中元素可正、可负、可0,给定一个整数k,求arr所有的子数组中累加和为k的最长子数组长度。
补充题目:
给定一个无序数组arr,其中元素可正、可负、可0。求arr所有的子数组中正数与负数个数相等的最长子数组长度。
补充题目:
给定一个无序数组arr,其中元素只是1或0,求arr所有的子数组中0和1个数相等的最长子数组长度。
原问题思路:时间O(N)、空间O(N)
s【i】代表子数组arr【0……i】所有元素的累加和。
arr【j……i】= s【i】- s【j】
题目要求的是若arr【j……i】==k,求最长的j-i+1
比如:arr = 【5,1,2,3,3】,k=6。
s[3] = 11,s[0] =5,sum(arr 【1:3】)= s[3] - s[0] = 6,长度为3
s[4] = 14,s[2] = 8, sum(arr 【3:4】)= s[4] - s[2] = 6,长度为2
结果为3
采用字典存储s
代码:
def maxLen(arr,k): if not arr or len(arr) == 0: return 0 dic = {} dic[0] = -1 res , nsum = 0 , 0 for i in range(len(arr)): nsum += arr[i] if (nsum - k) in dic: res = max(i - dic[nsum - k],res) if nsum not in dic: dic[nsum] = i return res arr = [5,1,2,3,3] k = 6 maxLen(arr,k)
补充问题思路:

12、未排序数组中累加和小于或等于给定值的最长子数组长度
给定一个无序数组arr,其中元素可正、可负、可0,给定一个整数k。求arr所有的子数组中累加和小于或等于k的最长子数组长度。
例如:arr = [3,-2,-4,0,6],k = -2,相加和小于或等于-2的最长子数组为{3,-2,-4,0},所以结果返回4。
思路:
题目要求的是:若arr【i……j】<= k,求最长的j-i+1。
arr【i……j】 = s[j] - s[i] ,(s[i] 表示 arr[0……i] 的值)
故判断 s[j] - s[i] <= k,即 判断 s[j] - k <= s[i]。
对于s[j] - k 找到第一个s[i] >= s[j] - k,就是最长的j-i+1。故创建一个辅助的列表helper,存储s[i] 当前出现的最大值。例如:arr = [1,2,-1,5,-2],k= -2 ,则 s[i] 列表为 [ 0,1,3,2,7,5],则helper = 【0,1,3,3,7,7】
比如当 j = 3时,【查找用二分法,时间复杂度为O(logN)】要找到 比 arr[3] - k = 5 大的第一个 s[i] 所在的位置i,所求的结果就为 j - i+ 1。借助helper辅助列表可知,第一个比5大的数为7,在 i = 4的位置,此时 表示遍历到 j = 3但只有在i=4时才能找到比5大的数,故j-i+1=0表示 arr【0……3】没有比 k小于或等于的数。
总结步骤:
1、创建一个辅助列表。
2、遍历数组,计算s[i] ,采用二分法查找辅助列表,找到第一个比s[i] - k大的数。
代码:
def maxLen(arr,k): if not arr or len(arr) <= 0: return 0 helper = [0] * (len(arr)+1) nsum = 0 for i in range(len(arr)): nsum += arr[i] helper[i+1] = max(nsum,helper[i]) nsum = 0 res = 0 pre = 0 nlen = 0 for i in range(len(arr)): nsum += arr[i] tmp = getcurMax(helper,nsum - k) nlen = 0 if tmp == -1 else (i-tmp + 1) res = max(res,nlen) return res def getcurMax(arr,nsum): left = 0 right = len(arr) - 1 res = -1 while left <= right: mid = (left + right) //2 if arr[mid] >= nsum: right = mid - 1 res = mid else: left = mid + 1 return res arr = [-1,-2,-1,-5,-2] k = -2 maxLen(arr,k)
13、计算数组的小和

思路:时间复杂度O(NlogN),空间O(N)
15、奇数下标都是奇数或偶数下标都是偶数
给定一个长度不小于2的数组arr,实现一个函数调整arr,要么让所有的偶数下标都是偶数,要么让所有的奇数下标都是奇数。
思路:时间O(N),空间O(1)
设置三个变量,even下标、odd下标、end下标
只要arr【end】 是偶数,就将arr【end】和arr【even】交换,even+=2.
同样,arr【end】 是奇数,就将arr【end】和arr【odd】交换,odd+=2.
代码:
def test(arr): if not arr or len(arr) <= 1: return arr even = 0 odd = 1 end = len(arr) - 1 while even < len(arr) and odd < len(arr): if arr[end] % 2 == 0: arr[end] , arr[even] = arr[even] , arr[end] even += 2 elif arr[end] % 2 == 1: arr[end] , arr[odd] = arr[odd] , arr[end] odd += 2 return arr arr = [1,8,3,2,4,6] test(arr)
16、子数组的最大累加和问题
给定一个数组arr,返回子数组的最大累加和。
例如,arr= 【1,-2,3,5,-2,6,-1】,所有的子数组中,【3,5,-2,6】可以累加出最大的和12,所以返回12.
时间O(N),空间O(1):设置一个cur和变量,一旦cur小于0,cur从0开始加当前位置的值。
import sys def test(arr): if not arr or len(arr) == 0: return 0 res = -sys.maxsize cur = 0 for i in range(len(arr)): cur += arr[i] res = max(res,cur) cur = 0 if cur<0 else cur return res arr = [1,-2,3,5,-2,6,-1] test(arr)
17、子矩阵的最大累加和问题
给定一个矩阵matrix,其中的值有正、有负、有0,返回子矩阵的最大累加和。
例如,矩阵matrix为:

思路:时间O(N3),空间O(N)
对于每一行都有以下操作:for i in range(len(arr))
for j in range(i ,len(arr)):
- 有一行时,子数组最大和和上题一样。
- 有两行时,两行矩阵最大值为行对应的列相加:如:
【64,-40,64】
【-81,-7,66】
变成 s =【-17,-47,130】,此时该子数组最大和为130【for k in range(len(arr[0]))】
- 有三行时,与两行的处理方式一样
- ……
代码:
import sys def maxSum(arr): if not arr or len(arr) == 0 or len(arr[0]) == 0: return 0 res = - sys.maxsize cur = 0 for i in range(len(arr)): s = [0] * len(arr[0]) for j in range(i , len(arr)): cur = 0 for k in range(len(arr[0])): s[k] += arr[j][k] cur += s[k] res = max(res,cur) cur = 0 if cur < 0 else cur return res arr = [[-90,48,78],[64,-40,64],[-81,-7,66]] maxSum(arr)
19、数组中子数组的最大累乘积

思路:时间复杂度O(N)、空间复杂度O(1).
- 可能是max * arr[i]
- 可能是min * arr[i],因为数组中可能包含负数,负负得正
- 可能是arr[i],因为以arr[i-1]结尾的最大乘积可能小于1
代码:
def maxMul(arr): if not arr or len(arr) == 0: return 0 maxMul = arr[0] minMul = arr[0] res = 0 for i in range(1,len(arr)): maxMul = maxMul * arr[i] minMul = minMul * arr[i] maxMul = max(maxMul , minMul ,arr[i] ) minMul = min(maxMul , minMul , arr[i] ) res = max(res , maxMul) return res
20、数组中三个数的最大累乘积
思路:时间复杂度O(N)、空间复杂度O(1).
找到三个最大的数max1,max2,max3 和两个最小的数 min1 ,min2 ,min3 ,返回 max( max1*max2*max3 , max1 * min1 * min2)
21、边界都是1的最大正方形大小
给定一个N*M的矩阵matrix, 在这个矩阵中, 只有0和1两种值, 返回边框全是1的最大正方
形的边长长度。
例如:
0 1 1 1 1
0 1 0 0 1
0 1 0 0 1
0 1 1 1 1
0 1 0 1 1
其中, 边框全是1的最大正方形的大小为4*4, 所以返回4
思路1:时间O(N4),枚举所有正方形,判断边框是否都为1
1.矩阵中一共有N*N个位置。O(N2)
2.对每一个位置都可以成为边长为N~1的正方形左上角。比如,对于(0,0)位置,依次检查是否是边长为5的正方形的左上角,然后检查边长为4、3等。O(N)
3.如何检查一个位置是否可以成为边长为N的正方形的左上角?遍历这个边长为N的正方形边界看是否只由1组成,也就是走过四个边的长度(4N)。O(N)
总的时间复杂度:O(N2)*O(N)*O(N)=O(N4)
思路2:时间复杂度为O(N3),以空间换时间的做法。
采用预处理矩阵的方法,同样也是枚举所有的正方形,但是判断该正方形是否符合规则是,是O(1)的时间复杂度,所以当M=N时,这是O(N^3)时间复杂度。
用与原矩阵同样大小的两个矩阵,一个为right,一个为down,
right[i][j]的值表示从位置(i,j)向右出发有多少个连续的1。
down[i][j]的值表示从位置(i,j)向下出发有多少个连续的1。
right和down的计算过程:从右到左,从下到上依次填好两个矩阵。
- 从矩阵的右下角(n-1,n-1)位置开始计算,如果matrix[n-1][n-1]=1,那么,right[n-1][n-1]=1,down[n-1][n-1]=1,否则都等于0。
- 从右下角向上计算,即在matrix最后一列上计算,位置就表示为(i,n-1)。对right来说,最后一列的右边没有内容,所以,如果matrix[i][n-1]=1, right[i][n-1]=1并且down[i][n-1]=down[i+1][n-1]+1,否则right[i][n-1]=0并且down[i][n-1]=0。
- 从右下角向左计算,即在matrix最后一行上计算,位置就表示为(n-1,j)。对down来说,最后一行的下边没有内容,所以,如果matrix[n-1][j]=1, down[n-1][j]=1并且right[n-1][j]=down[n-1][j+1]+1,否则right[n-1][j]=0并且down[n-1][j]=0。
- 剩下的位置都是既有右,又有下,假设位置(i,j):
- if matrix[i][j]=1, then right[i][j+1]=right[i][j]+1,down[i][j]=down[i+1][j]+1.
- if matrix[i][j]=0,then right[i][j]=0,down[i][j]=0.
22、不包含本位置值的累乘数组
给定一个整型数组arr,返回不包含本位置值的累乘数组。
例如,arr = [2, 3, 4, 1],返回[12, 8, 24, 6],即除自己以外,其他位置上的累乘。
【要求】
- 时间复杂度O(N)
- 除需要返回的结果数组外,额外空间复杂度O(1)。
不用除法思路:
分别使用辅助两个数组left和right,其中left表示数组从左到右的累乘结果(即left[i] = arr[0…i]的累乘);相反,right表示数组从右到左的累乘结果。那么对于结果数组res,res[i] = left[i-1] * right[i+1]。
实际上,并不需要额外声明两个辅助数组。可以复用结果数组res,即先将res当辅助数组用,再把res调整为结果数组即可。具体实现见如下代码:
def product2(arr): if arr == None or len(arr) < 2: return res = [0 for i in range(len(arr))] res[0] = arr[0] for i in range(1, len(res)): res[i] = res[i-1] * arr[i] tmp = 1 for i in range(len(arr)-1, 0, -1): res[i] = res[i-1] * tmp tmp *= arr[i] res[0] = tmp return res arr = [2,3,1,4] product2(arr)
23、数组的partition调整
给定一个有序数组arr,调整arr使得这个数组的左半部分没有重复部分且升序,而不用保证右部分是否有序。
例如:arr=[1,2,2,2,3,3,4,5,6,6,7,7,8,8,9,9],调整之后arr=[1,2,3,4,5,6,7,8,9…]。
要求:
时间复杂度O(N),额外空间复杂度O(1)
思路:两个变量
变量u表示:arr[0……u]上是无重复且升序的,初始u=0
变量i表示:arr[u+1……i]不保证无重复但升序的区域,i是遍历到的结果,初始时i=1.
i向右移动,若arr【i】!=arr【u】,则将arr【i】加入arr【0……u】区域内,即arr【u+1】和arr【i】交换。
直到遍历结束
代码:
def patition(arr): if not arr or len(arr)==1: return arr u , i = 0 , 1 while i < len(arr): if arr[i] != arr[u]: arr[i] , arr[u+1] = arr[u+1] , arr[i] u += 1 i += 1 return arr arr = [1,2,2,2,3,3,4,5,5,6,6,7,8,9,9] patition(arr)
补充题目:
给定一个数组arr,其中只可能含有0、1、2三个值,请实现arr的排序。
另外一种问法:有一个数组,其中只有红球、篮球和黄球,请实现红球全放在数组的左边,篮球放在中间,黄球放在右边。
另外一种问法:有一个数组,再给定一个值K,请实现比K小的数都放在数组的左边,等于K的值都放在数组的中间,比K大的数都放在数组的右边。
思路:
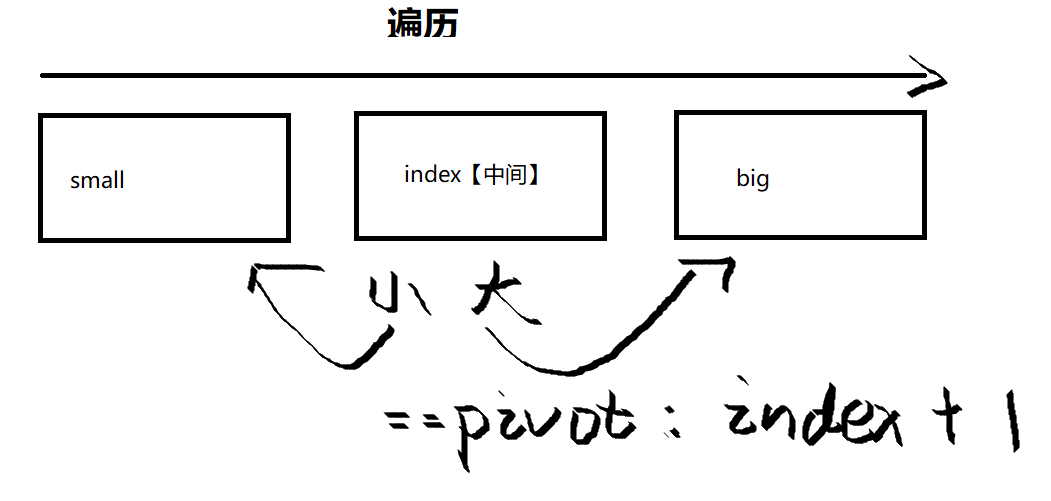
left变量:表示左区arr【0……left】都是0,left初始为-1
index变量:表示中区arr【left+1……index】都是1,index初始为0
right变量:表示右区arr【right……N-1】都是2,right初始为N-1.
index表示从左往右遍历的位置:
arr【index】== 1,留在中区,index+=1
arr【index】==0,加入左区,即arr【left+1】和arr【index】交换,left+=1,index+=1
arr【index】== 2,加入右区,即arr【right-1】和arr【index】交换,right-=1。
当index == right,停止遍历,因为中区和右区对接了。
代码:
def patition(arr): if not arr or len(arr)==1: return arr left , index , right = -1 , 0 , len(arr) while index != right: if arr[index] == 0: arr[left+1] , arr[index] = arr[index] , arr[left+1] left += 1 index += 1 elif arr[index] == 1: index += 1 elif arr[index] == 2: arr[right - 1] , arr[index] = arr[index] , arr[right-1] right -= 1 return arr arr = [1,0,2,2,1,1,0,2,1,2] patition(arr)
25、数组中未出现的最小正整数
给定一个无序整型数组arr,找到数组中未出现的最小正整数。
举例:
arr = 【-1,2,3,4】。返回1
arr = 【1,2,3,4】。返回5.
思路:时间O(N),空间O(1)
分析:
假如arr有序,则:
(1) arr为整数1,2,3…N,N+2,N+3……的一个随机排列,那个未出现的最小正整数就是N+1。
【设置left变量表示已经有序的N个数 arr [0:N-1] 】
(2) arr中有小于1或者大于N或者重复的数出现(我们称之为“不合法”的数),则未出现的最小正整数一定在1到N中间(因为数组一共只有N个数,如果出现不合法的数,则出现的1到N之间的数的个数一定小于N,故一定有没有出现的数)。
【设置right变量,初始N+2, 表示还可以有序的arr [ N:N+2 ]】
【比如:发现 arr[N](即N+2)合法但位置不理想,将N+2换到它理想的位置,然后将N+3换到该位置 arr[ N ],继续比较N+3是不是合法且理想,发现并不合法,合法区间right-1变成 arr[ N:N+1 ] 】
做法:
(1) 先设置两个变量L,R。初始值:L=0,R=len(arr)
- L表示已经从1到L已经出现(左边界),L的初值为0。
- 如果一个数字过大(不合法),就会被扔掉,用R表示这个右边界,即大于R的数会被扔掉。R的初值为N,表示从1到R的元素都不会被扔掉,大于R的就会被扔掉。但是这个R的值是变化的,如果L+1到R中有一个元素不合法,那么R--,因为最多只能放下R-1个合法数。
也就是说,1到L上的数已经出现,[L+1,R]区间上的数未出现但可能会出现。
(2)遍历数组:
1》当 L 的位置值等于L+1,表示得到想要的,故L ++
2》三种不合法情况:都需R--
- 小于左边的数:当 L 的位置值< L 时,表示 L 位置的值已经存在,所以这个数组不会存在到 R 的值了 so R--
- 大于右边的数:当 L 的位置值> R 时,表示 L 的位置已经超过 R ,所以数组不会存在到 R 的值了, so R--
- 左边区域重复的数:当 L 的位置值和 (L 值的位置-1)的的位置值相等时,所有数组不会存在到 R 的值了,so R-- 【即L位置的值已经存在左区域已经出现的数中了,两个一样的值,比如 [1,2,3,2,4] ,第二个2已经重复了[1,2,3]中的2了 】
3》合法但位置不理想:else,将 arr【L】 交换到理想位置,理想位置的值换到 L 位置来,继续判断 L 位置的值。
代码
def missNum(arr): if not arr: return 1 left , right = 0 , len(arr) while left < right: if arr[left] == left + 1: left += 1 elif arr[left] <= left or arr[left] > right or arr[left] == arr[arr[left]-1]: right -= 1 arr[left] = arr[right] #right-=1后合法区域不包括arr【right】了,将arr[right]换到left位置继续判断 else: #arr[left]理想位置为arr[left]-1,将arr[arr[left]-1]换到left位置继续判断 arr[left] , arr[arr[left] - 1] = arr[arr[left]-1] , arr[left] return left + 1 arr = [1,3,-2,4,5] missNum(arr)
26、题目:查找满足条件的二维数组最大值和次大值之和(RMQ算法)
在一个二维坐标数组中,第一列x为坐标值,第二列y为金额,求满足|x1-x2| >= d,求(y1 + y2)和最大的值。【两个变量满足坐标值大于等于d条件,且其金额之和最大】,返回金额和的值。
如:d = 3 , 输入 [[1,1],[3,5],[4,8],[6,4],[10,3],[11,2]]。输出:11,因为 [4,8] 和[10,3],|4 - 10| >= d, 8 + 3 =11金额最大。
思路:
先将坐标排序,然后将金额从后面开始,从大到小放入栈中。
接着,从前往后遍历,采用一个prefix存储前面的最大值,同时一旦遇到满足d条件的栈中的第一个数,更新和最大值。
代码
def solve(arr,d): #将arr按坐标值排序 arr.sort(); #suffix是将arr按金额从大到小存入栈中,如arr中金额为[1,5,8,3,4,2] ,则suffix为[8,8,8,4,4,2] suffix = [0] * len(arr) suffix[len(arr) - 1] = arr[len(arr) - 1][1] for i in range(len(arr) - 2,-1,-1): suffix[i] = suffix[i + 1] if suffix[i + 1] > arr[i][1] else arr[i][1] #prefix存前面最大的数 prefix = 0 # pos为当前第一个满足arr[pos] > arr[i]的数 pos = 0 ret = 0 for i in range(len(arr)): prefix = prefix if prefix > arr[i][1] else arr[i][1] while pos < len(arr) and arr[pos][0] - arr[i][0] < d: pos += 1 if pos < len(arr): ret = ret if ret > prefix +suffix[pos] else prefix + suffix[pos] return ret arr = [[1,1],[3,5],[4,8],[6,4],[10,3],[11,12]] d = 3 solve(arr,d)
27、题目:奇数在前,偶数在后,且原本位置不变,即稳定的,奇偶数
输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有的奇数位于数组的前半部分,所有的偶数位于数组的后半部分,并保证奇数和奇数,偶数和偶数之间的相对位置不变。
思路:
代码:
def reOrderArray(self, array): # write code here if len(array) <= 1: return array flag = -1 for i in range(len(array)): if (array[i] % 2 == 0) and flag == -1: flag = i elif (array[i] % 2 == 1) and flag != -1: array.insert(flag,array[i]) flag += 1 del array[i+1] return array
28、数组中的逆序对
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007
输入:1,2,3,4,5,6,7,0
输出:7
1、暴力求解思路:
遍历两遍,针对每一个数都找后面比其小的数。
2、归并排序思路:
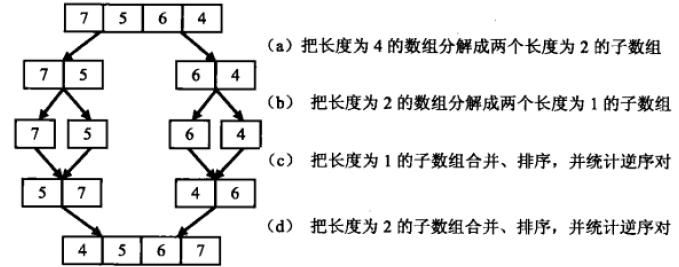
逆序对的总数=左边数组中的逆序对的数量+右边数组中逆序对的数量+左右结合成新的顺序数组时中出现的逆序对的数量
代码:
class Solution: def __init__(self): self.P = 0 def InversePairs(self, data): # write code here if not data: return 0 def merge(arr1,arr2): res = [] i , j = 0 , 0 while i < len(arr1) and j < len(arr2): if arr1[i] <arr2[j]: res.append(arr1[i]) i += 1 else: res.append(arr2[j]) j += 1 self.P += (len(arr1)-i) res.extend(arr1[i:]) res.extend(arr2[j:]) return res def fen(data): if len(data)<=1: return data mid = len(data)//2 left = fen(data[:mid]) right = fen(data[mid:]) return merge(left,right) fen(data) return self.P % 1000000007
3、树状数组思路:
思路1:离散化 + 树状数组
离散化:

树状数组:
可以把数一个个插入到树状数组中, 每插入一个数, 统计比他小的数的个数,对应的逆序为 i- getsum( data[i] ),其中 i 为当前已经插入的数的个数, getsum( data[i] )为比 data[i] 小的数的个数,i- getsum( data[i] ) 即比 data[i] 大的个数, 即逆序的个数。最后需要把所有逆序数求和,就是在插入的过程中边插入边求和。

代码:
#include <iostream> #include <stdio.h> #include <stdlib.h> #include <algorithm> #include <string.h> using namespace std; const int maxn=500005; int n;int aa[maxn]; //离散化后的数组 int c[maxn]; //树状数组 struct Node{ int v; int order; } in[maxn]; int lowbit(int x){ return x&(-x); } void update(int t,int value){ int i; for(i=t;i<=n;i+=lowbit(i)) { c[i]+=value; } } int getsum(int x){ int i; int temp=0; for(i=x;i>=1;i-=lowbit(i)) { temp+=c[i]; } return temp; } bool cmp(Node a ,Node b){ return a.v<b.v; } int main(){ int i,j; while(scanf("%d",&n)==1 && n) { //离散化 for(i=1;i<=n;i++) { scanf("%d",&in[i].v); in[i].order=i; } sort(in+1,in+n+1,cmp); for(i=1;i<=n;i++) aa[in[i].order]=i; //树状数组求逆序 memset(c,0,sizeof(c)); long long ans=0; for(i=1;i<=n;i++) { update(aa[i],1); ans+=i-getsum(aa[i]); } cout<<ans<<endl; } return 0; }
另一种思路:

这样直到把最小元素放完,累加每次放元素是该元素前边已放元素的个数,这样就算出总的逆序数来了
在统计和计算每次放某个元素时,该元素前边已放元素的个数时如果一个一个地数,那么一趟复杂度为O(n),总共操作n趟,复杂度为O(n^2),和第一种方法的复杂度一样了,那我们为什么还用这么复杂的方法
当然,在每次统计的过程中用树状数组可以把每一趟计数个数的复杂度降为O(logn),这样整个复杂度就变为O(nlogn)
将序列中的每个数按照从大到小的顺序插入到树状数组中,给当前插入节点及其父节点的个数加1,然后统计该节点下边及右边放置元素的个数
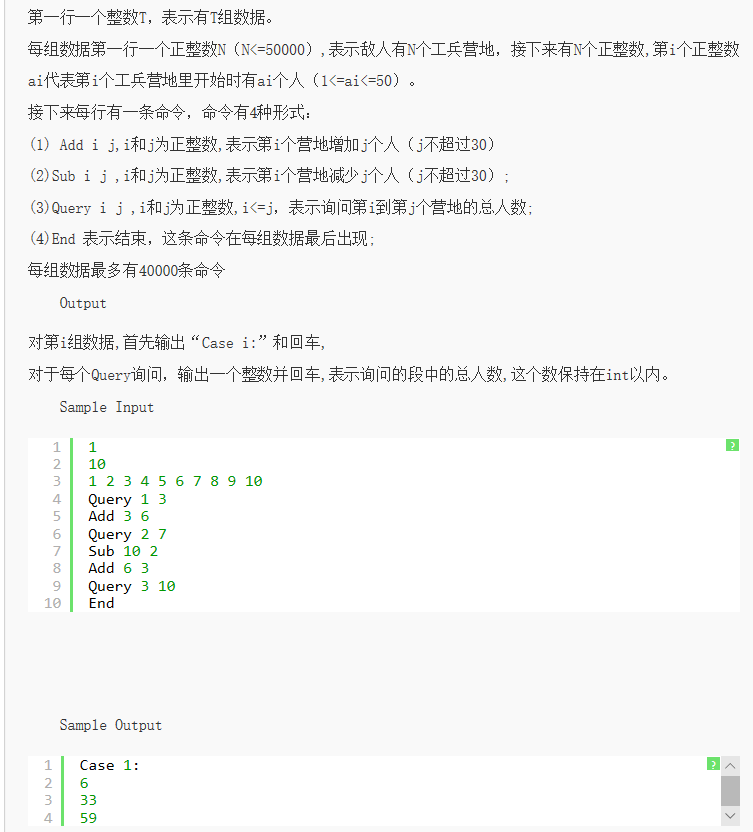
29、题目:RMQ算法:
题意:一维线性的直线上,排列着n个兵营,初始每个兵营有固定的人数,有两个操作:一个是添加,把某个兵营增加人数d;二是询问,求某两个兵营之间所有兵营的总人数之和。
代码:
