前缀和与差分
前缀和与差分
一维前缀和
1、用途
\(O(1)\)区间查询
2、原理
设\(S[n]\)为数列\(a\)的前\(n\)项和，那么\(a[l:r]\)的和为\(S[r]-S[l-1](1\le l\le r\le n)\)。
转移方程：\(S[i]=S[i-1]+a[i]\)
3、复杂度
预处理：\(O(n)\)
查询：\(O(1)\)
4、模板
for (int i = 1; i <= n; ++i) S[i] = S[i - 1] + a[i]; //build
cout << S[r] - S[l - 1] << endl; //query
5、备注
①下标一定从1开始。
二维前缀和
1、用途
\(O(1)\)查询子矩阵和
2、原理
设以\((1,1),(i,j)\)为主对角线两个端点的子矩阵的元素和为\(S[i][j]\)。那么以\((x_1,y_1),(x_2,y_2)\)为主对角线两个端点的子矩阵和为\(S[x_2][y_2]-S[x_1-1][y_2]-S[x2][y_1-1]+S[x_1-1][y_1-1]\)，其中\(1\le x_1\le x_2\le i,1\le y_1\le y_2\le j\)。
转移方程：\(S[i][j]=S[i-1][j]+S[i][j-1]-S[i-1][j-1]+a[i][j]\)
用图表示比较直观。
假设我们要求红色部分的和。
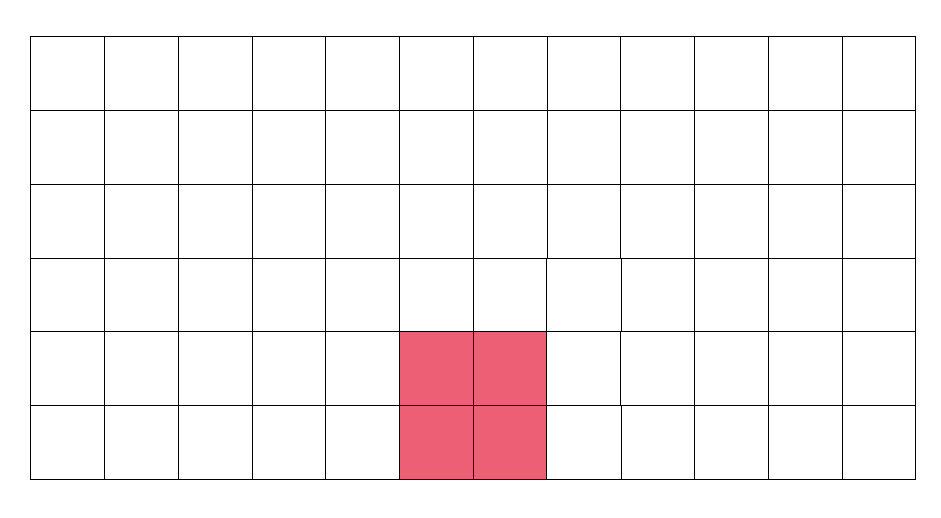
那么我们可以先计算出整个绿色区域的和。
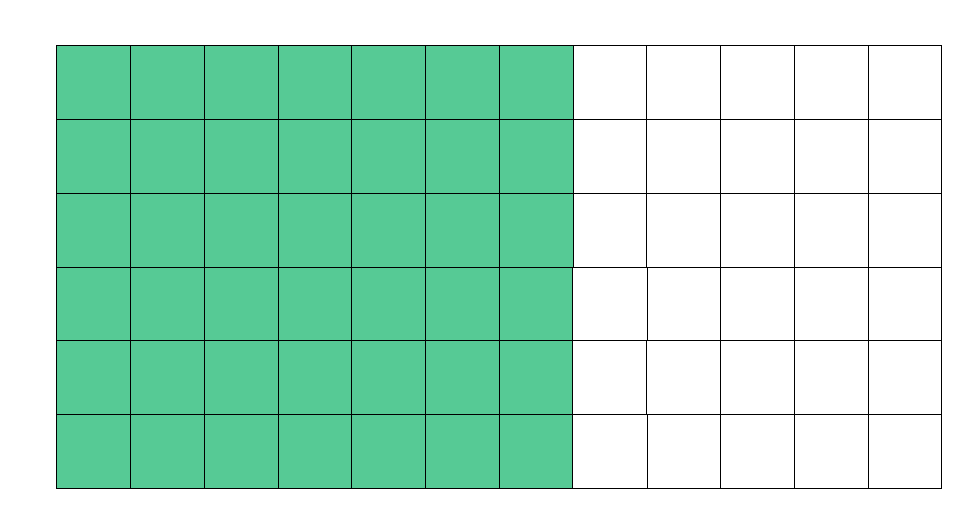
之后减去不必要的部分，这里用黄色表示。
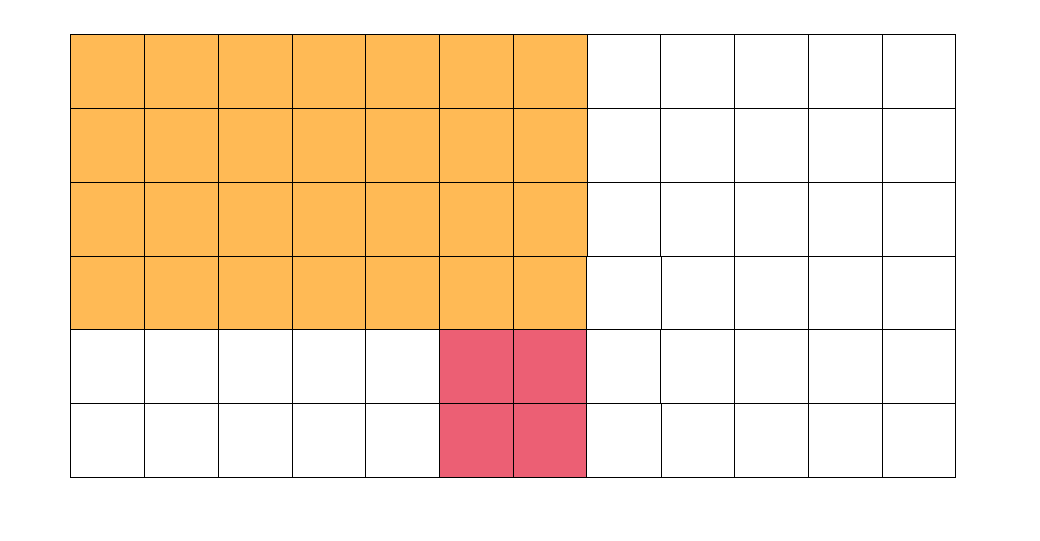
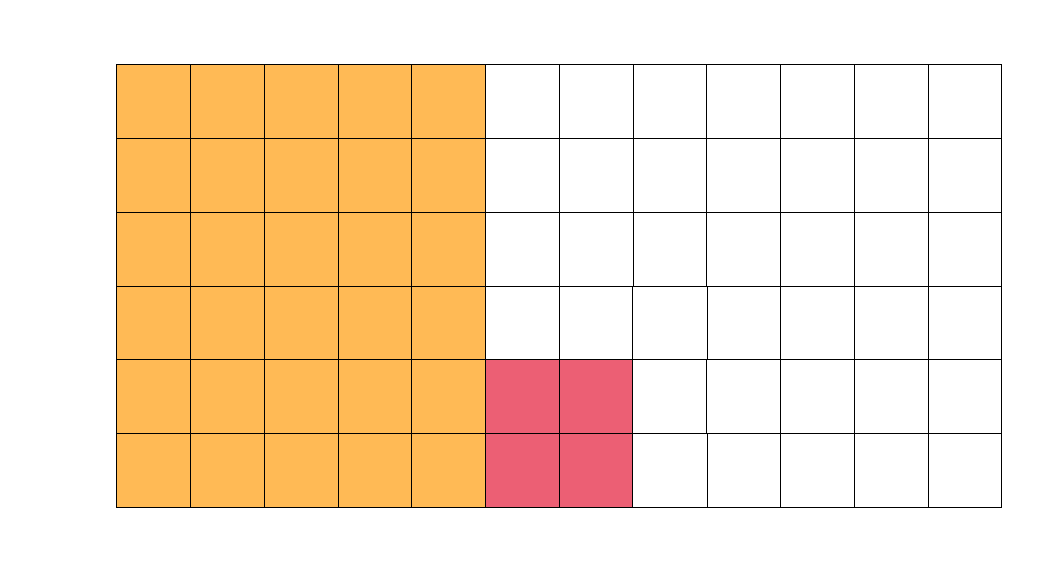
但是注意到灰色部分减去了两次，因此加上一次。这就是查询的原理。
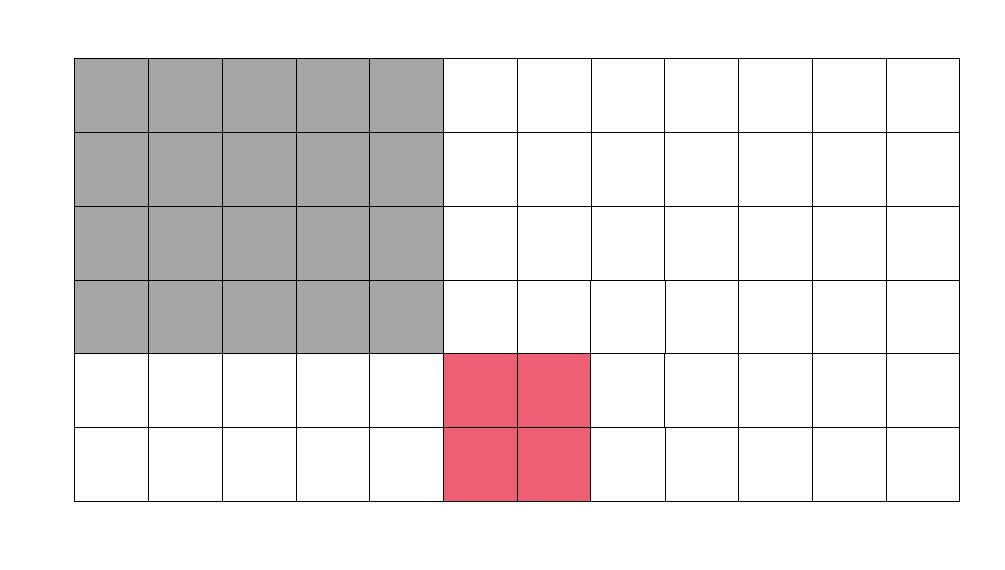
转移方程也类似。
3、复杂度
预处理：\(O(mn)\)
查询：\(O(1)\)
4、模板
for (int i = 1; i <= n; ++i) //build
for (int j = 1; j <= m; ++j)
S[i][j] = S[i - 1][j] + S[i][j - 1] - S[i - 1][j - 1] + a[i][j];
cout << S[x2][y2] - S[x1 - 1][y2] - S[x2][y1 - 1] + S[x1 - 1][x1 - 1] << endl; //query
5、备注
①下标一定从1开始。
一维差分
1、用途
区间修改，区间查询
2、原理
假设对\(a[l:r]\)同时进行\(+d(d\in \mathbb R)\)操作，观察到\(\forall i\in (l,r],a[i]-a[i-1]\)不变，仅有\(a[l]-a[l-1]\)相比原来的值多\(d\)，并且\(a[r+1]-a[r]\)相比原来的值少\(d\)。
于是定义差分数组\(dif[i]\)，差分数组的前缀和为\(sum[i]\)，修改后的元素大小为\(a'[i]=a[i]+sum[i]\)。
\(sum[i]\)可以看成\(a[i]\)的增量。
由\(a'[l]=a[l]+sum[l],a'[l-1]=a[l-1]+sum[l-1]\)，两式相减得\(dif[l]=d\)。同理\(dif[r+1]=-d\)。
于是\([l,r]\)区间修改可以看成\(dif[l]+=d,dif[r+1]-=d\)。查询时只要对\(dif\)求前缀和，再加上原来的值即可。
画图比证明直观。图与下面二维差分类似，就不另画了。
3、复杂度
区间修改：\(O(1)\)
区间查询：\(O(n)\)
4、模板
dif[l] += d, dif[r + 1] -= d; //build
for (int i = 1, s = 0; i <= n; ++i)
s += dif[i], cout << a[i] + s << endl; //query
5、备注
①下标一定从1开始。
②差分数组要比给的数据上限开得更大一点。
③由于区间查询复杂度比较高，一般在多修改少查询的情况下使用。
④只支持简单的加减修改操作。
二维差分
1、用途
子矩阵修改，子矩阵查询
2、原理
类比一维差分定义二维差分数组\(dif[i][j]\)，以差分数组的二维前缀和表示\((i,j)\)的增量。
考察修改差分数组的值对原数组的贡献。若\(dif[i][j]+=d\)，则对于\(\forall x,y\)，若满足\(x\ge i\)并且\(y\ge j\)，则\((x,y)\)处的值就都要加上\(d\)。
以图为例，假设表格表示差分数组。现在用红色表示在该格处进行修改。
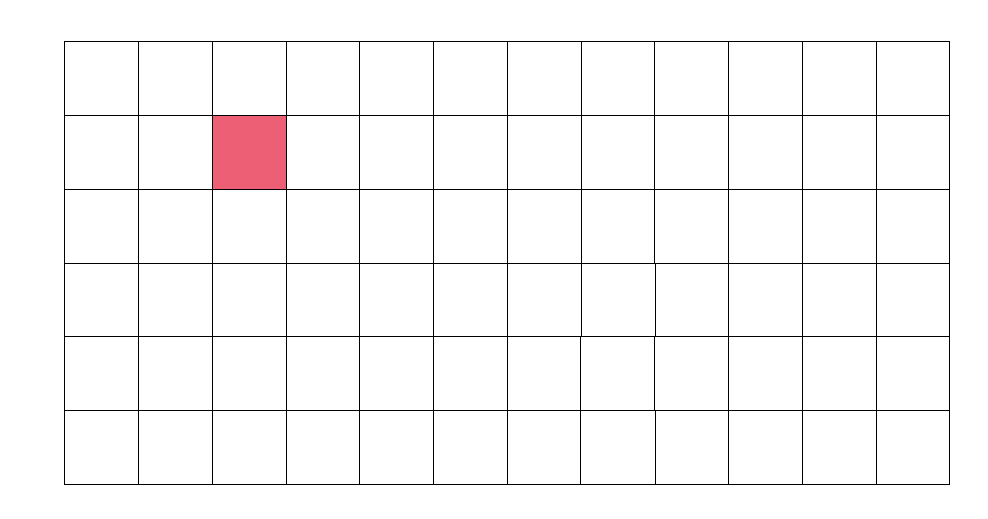
那么该格对于差分数组的贡献就是所有绿色的格子。
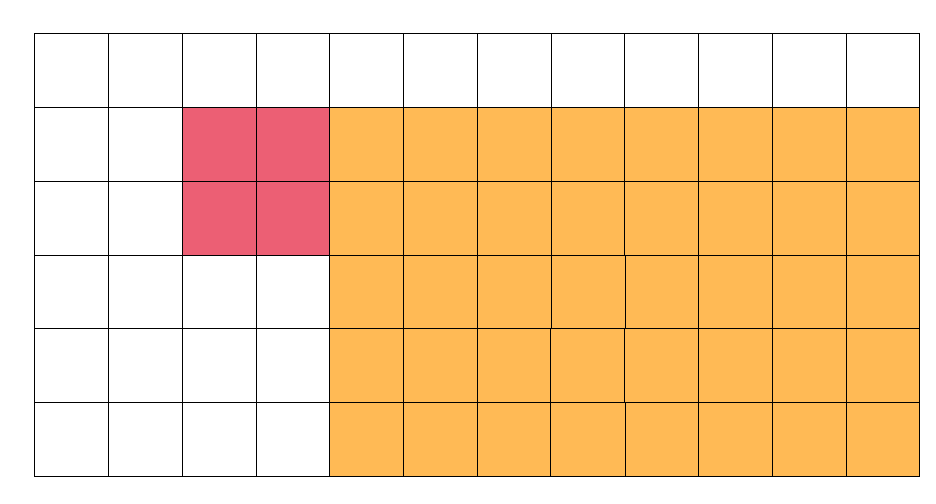
如果我们要修改如下图所示的红色区域：
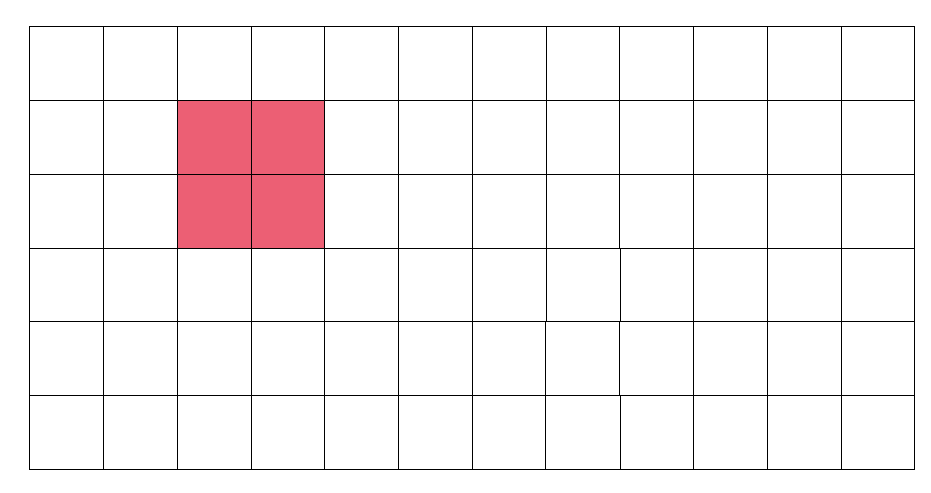
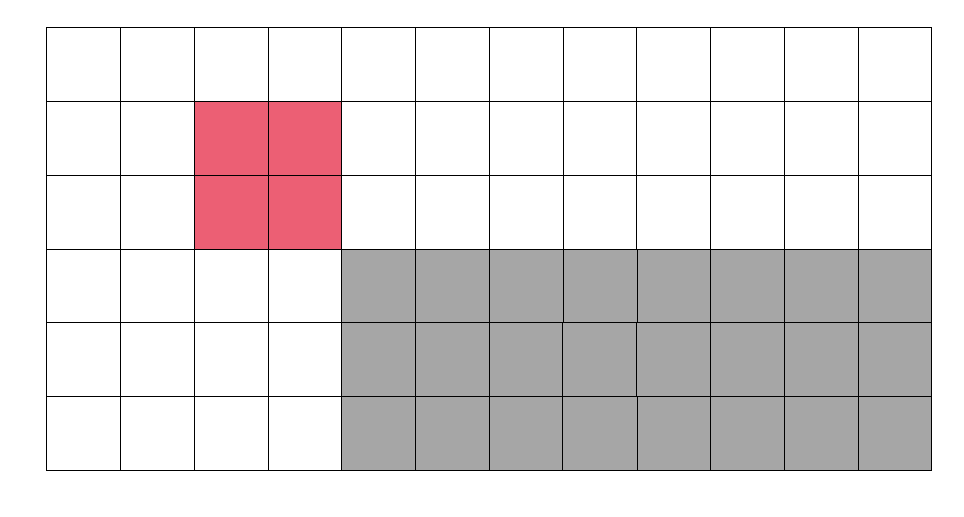
那么与二维前缀和类似，我们可以先修改绿色的区域，再减去两个黄色的区域，最后补上减去两次的灰色区域。每次修改都在色块的左上角方格进行。
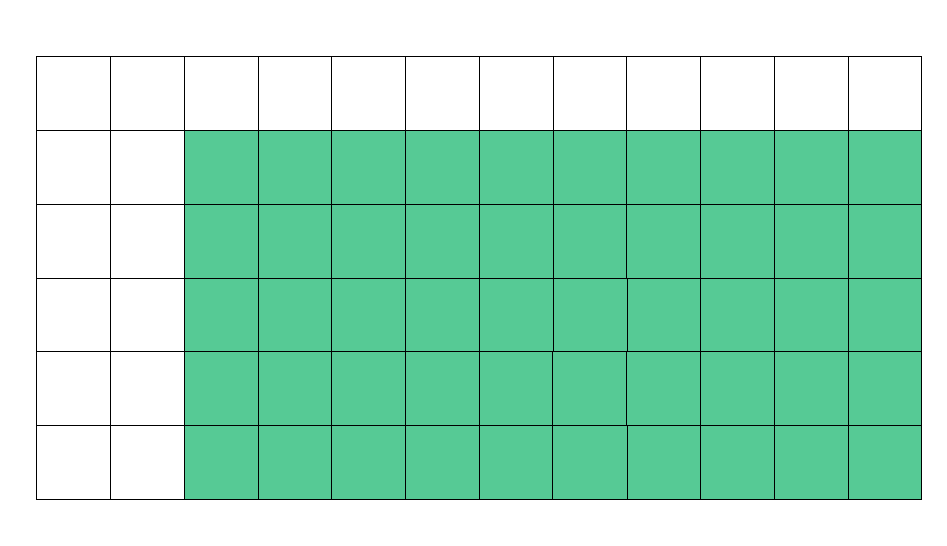
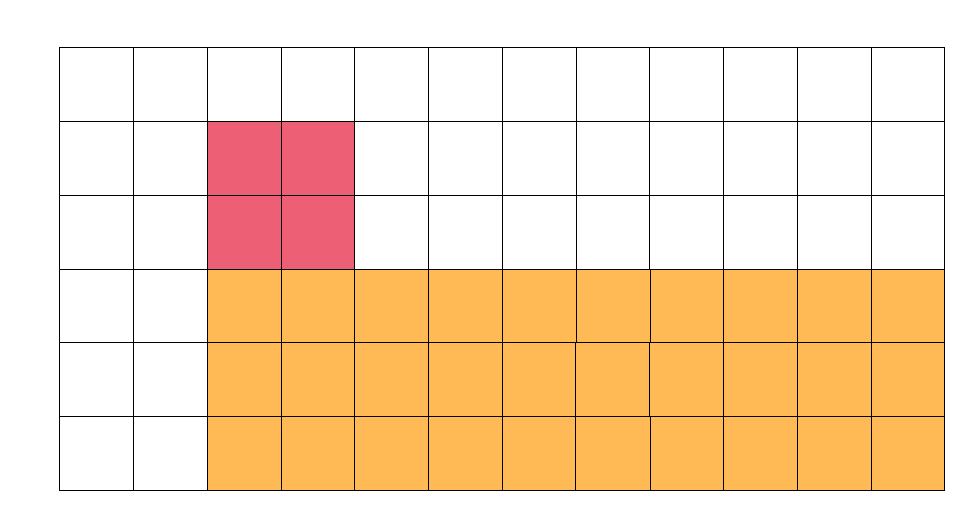
3、复杂度
子矩阵修改：\(O(1)\)
子矩阵查询：\(O(mn)\)
4、模板
dif[x1][y1] += d, dif[x2 + 1][y1] -= d, dif[x1][y2 + 2] -= d, dif[x2 + 1][y2 + 1] += d; //build
for (int i = 1; i <= n; ++i) //query
for (int j = 1; j <= m; ++j)
{
dif[i][j] += dif[i - 1][j] + dif[i][j - 1] - dif[i - 1][j - 1];
cout << a[i][j] + dif[i][j] << endl;
}
5、备注
①下标一定从1开始。
②差分数组要比给的数据上限开得更大一点。
③由于子矩阵查询复杂度比较高，一般在多修改少查询的情况下使用。
④只支持简单的加减修改操作。
