算法介绍(二分,冒泡,选择,插入;快排,堆排,归并)
1.概念
算法:一个计算过程(函数),或者说是解决问题的方法可以理解成一个算法
时间复杂度:用来估算算法运行时间的一个式子(单位)。一般来说,时间复杂度高的算法比复杂度低的算法慢
空间复杂度:用来估算算法占用内存的一个式子
1.1 常见时间复杂度按照效率排序
O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n2logn)<O(n3)
一般来说
循环减半的过程,时间复杂度通常是O(logn)
几次循环,时间复杂度就是n的几次方
1.2 案例
""" 一段有n个台阶组成的楼梯,小明从楼梯的最底层向最高处前进,它可以选择一次迈一级台阶或者一次迈两级台阶。问:他有多少种不同的走法? """
思路:
假设上 n 级台阶有 f(n)种方法,把这 n 种方法分为两大类,第一种最后一次上了一级台阶,这类方法共有 f(n-1)种,第二种最后一次上了两级台阶,这种方法共有 f(n-2)种,则得出递推公式f(n)=f(n-1)+f(n-2),显然,f(1)=1,f(2)=2,递推公式如下:
def steps(n): if n <= 2: return n else: return steps(n-1) + steps(n-2) print(steps(10))
这种方式简单,但是效率低,很有可能超出递归最大层数
我们可以考虑采用循环来做
1.3 二分排序法(时间复杂度O(logn))
这里针对的是一个有序列表,一般是在算法中输入该列表中某个数,然后输出这个数在列表中的位置,即索引
示意图:
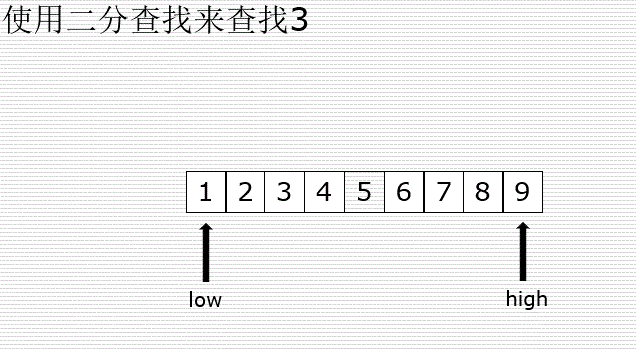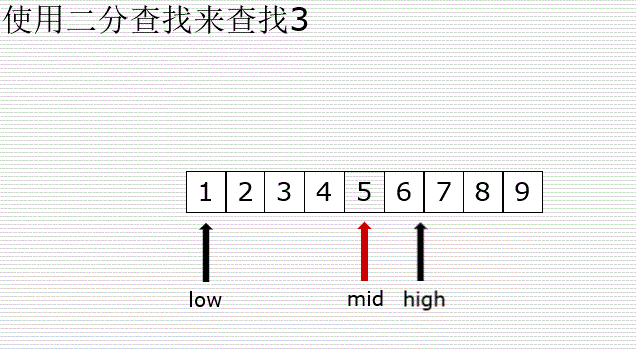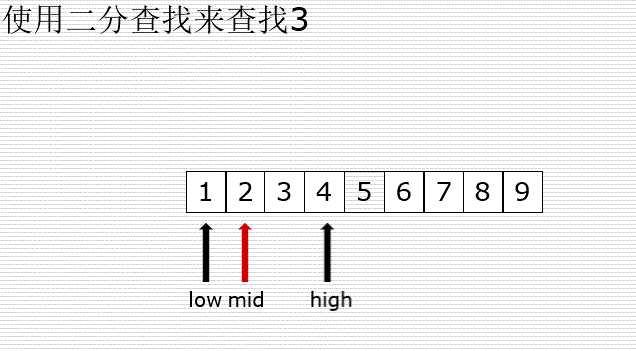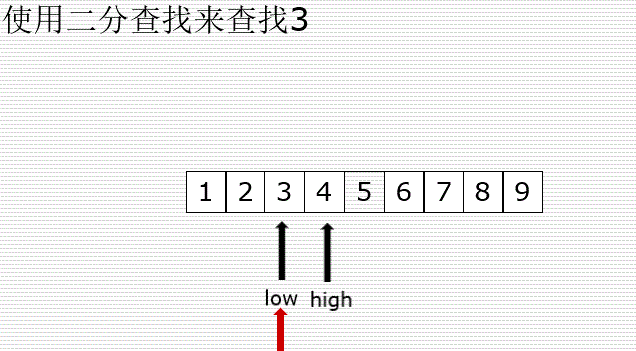
代码:
def bin_search(key, lis): low = 0 # 首 high = len(lis) - 1 # 尾 while low < high: mid = (low + high) // 2 if lis[mid] == key: # 命中 return mid elif lis[mid] > key: # key在左边,说明key的范围在low到mid-1之间 high = mid - 1 elif lis[mid] < key: # key在右边,说明key的范围在high+1到high之间 low = mid + 1
利用递归实现二分查找(可以使用bisect模块来实现):
def bin_search_2(key, lis, low, high): if low <= high: mid = (low + high) // 2 if lis[mid] == key: return mid elif lis[mid] > key: # 在左边,说明key在low和mid-1之间 return bin_search_2(key,lis,low, mid-1) else: # 在右边,说明key在mid+1和high之间 return bin_search_2(key,lis,mid+1,high) else: return
对于一个二维列表实现的二分查找:
li = [ [1, 3, 5, 7], [9,10,14,17], [18,22,25,30] ]
代码:
def binary_search_2d(li, val): left = 0 m = len(li) n = len(li[0]) right = m * n - 1 while left <= right: # 候选区非空 mid = (left + right) // 2 i = mid // n # 取整 j = mid % n # 取余 if li[i][j] == val: return i, j elif li[i][j] < val: left = mid + 1 # 更新候选区 else: # > right = mid - 1 # 更新候选区 return None print(binary_search_2d(li, 22))
2. 排序入门篇
2.1 冒泡排序(时间复杂度O(n**2))
针对的是列表中的两个相邻的数,如果前边比后面的大,则交换这两个数,如此持续进行
代码关键点在于几趟以及无序区
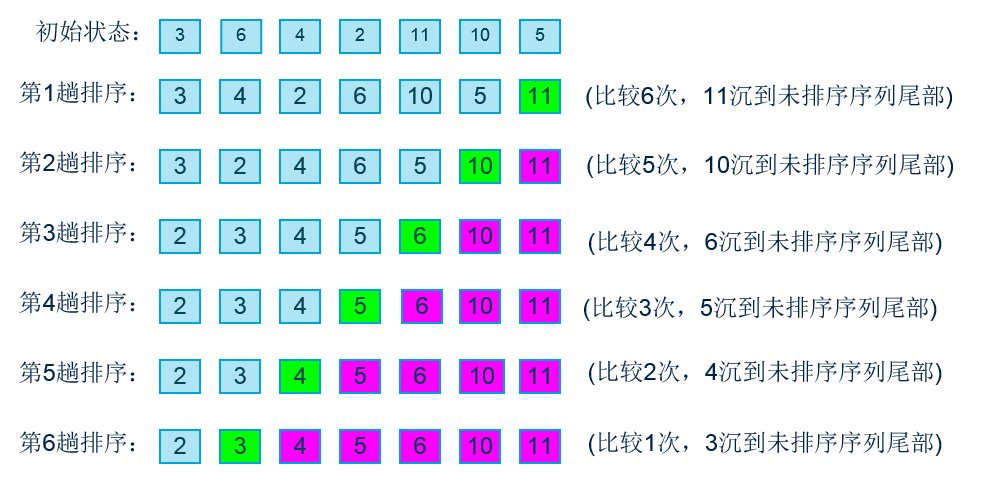
示例代码1:
def bubble_sort(lis): # j表示每次便利需要遍历的最小次数,它是逐渐减小的 for j in range(len(lis)-1,0,-1): for i in range(j): if lis[i] > lis[i+1]: lis[i],lis[i+1] = lis[i+1], lis[i] lis = [9,5,2,7,6,8,3,1,4] bubble_sort(lis) print(lis)
示例代码2:
import random def bubble_sort(li): for i in range(len(li)-1): # i表示第i趟 for j in range(len(li)-i-1): # j表示箭头的下标 if li[j] > li[j+1]: # 后面的数比前面的数大 li[j], li[j+1] = li[j+1], li[j] print(li) li = list(range(10)) random.shuffle(li) bubble_sort(li)
以上代码忽视了极端情况,从运行效率上来讲,我们还可以在做优化,排除已经是有序的列表
import random def bubble_sort_2(li): for i in range(len(li)-1): # i表示第i趟 exchange = False for j in range(len(li)-i-1): # j表示箭头的下标 if li[j] > li[j+1]: # 如果前面比后面大 li[j], li[j+1] = li[j+1], li[j] exchange = True if not exchange: return print(li) li = list(range(10)) random.shuffle(li) bubble_sort_2(li)
2.2 选择排序(时间复杂度O(n**2))
选择排序第一种代码:
一趟遍历记录最小的数,放到第一个位置;
再一趟遍历记录剩余列表中最小的数,继续放置;
关键点在于无序区以及最小数的位置
代码:
import random def select_sort(li): for i in range(len(li)-1): # i可以理解成趟数,这里看做索引也行 min_pos = i # 最小值默认为无序区第一个数 i for j in range(i+1, len(li)): if li[j] < li[min_pos]: min_pos = j li[i], li[min_pos] = li[min_pos], li[i] li = list(range(100)) random.shuffle(li) select_sort(li) print(li)
选择排序第二种代码:
这里我也可以先去查找数组中最小值的索引,然后再追加的方式来排序(好理解,但是代码量变大)
# 查找最小值的索引 def findSmanllest(arr): smallest = arr[0] smallest_index = 0 for i in range(1,len(arr)): # 这里应该是range(1,len(arr))还是range(len(arr))??尝试两个都可以 if arr[i] < smallest: smallest = arr[i] smallest_index = i return smallest_index # 返回数组中最小值的索引 # 进行排序 def selectionSort(arr): newarr = [] for i in range(len(arr)): smallest = findSmanllest(arr) newarr.append(arr.pop(smallest)) # 追加数组中指定索引的值 return newarr print(selectionSort([5,3,6,2,10,41,1]))
2.3 插入排序(时间复杂度O(n**2))
列表被分为有序区和无序区两个部分。最初有序区只有一个元素。
每次从无序区选择一个元素,插入到有序区的位置,直到无序区变空。(类似我们玩纸牌)
代码关键点在于我们摸到的牌,以及手里的牌
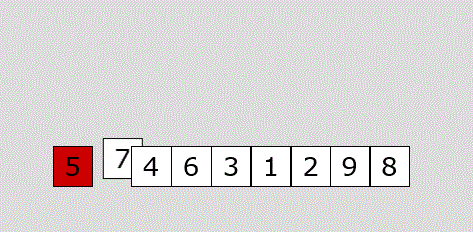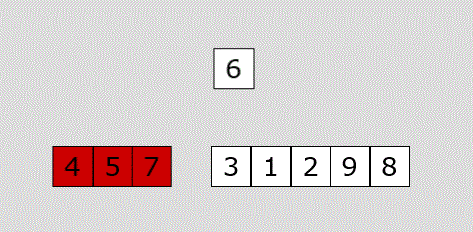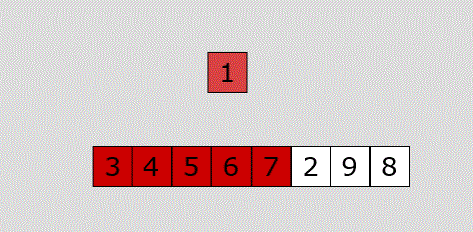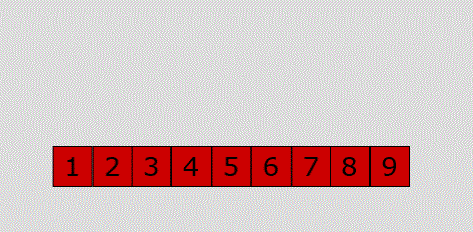
代码:
import random def insert_sort(li): for i in range(1, len(li)): # i表示摸到牌的位置,也表示趟 j = i - 1 # j是当前用来比较的牌 tmp = li[i] # 摸到的牌 while j >= 0 and li[j] > tmp: # 摸到的牌和他前面位置(前面位置必须大于等于0)的牌作比较 li[j+1] = li[j] # 前面的牌比手里的大,把它往后移 j -= 1 # 再去看前面那张牌 li[j+1] = tmp # 用来比较的牌比摸到的牌小,直接放到j+1的位置 li = list(range(100, -1, -1)) random.shuffle(li) insert_sort(li) print(li)
3. 排序升级篇
3.1 快排(时间复杂度O(n*log(n))) --->算法里面简单,也是必须要掌握的一个
取一个元素p(第一个元素),使元素p归位;
列表被p分成两部分,左边都比p小,右边都比p大;
递归完成排序。
该算法的关键点是先对数组进行整理,然后再做递归操作
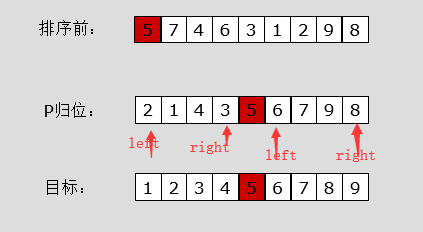
代码第一部分
def quick_sort(lis, left, right): if left < right: mid = partition(lis, left, right) # 返回中间这个值 quick_sort(lis, left, mid - 1) # 对左边的进行排序 quick_sort(lis, mid + 1, right) # 对右边的进行排序
但是怎么对它做p归位处理呢?这里我们先取出第一个数,即5,5的空位需要从右边往左找一个比5小的数填充,即2
2放在了5的空位上,现在需要再从左边取一个比5大的数放在2的空位上,即7
7放在了2的空位上,现在需要再从右边取一个比5小的数放在7的空位上,即1
---

代码第二部分(做归位处理)
def partition(lis, left, right): tmp = lis[left] # 先取出最左边这个数,存起来 while left < right: # 从右边找比tmp小的数 while left < right and lis[right] >= tmp: right -= 1 # 如果右边的数总比取出的数大,则往左前进一位继续找直到找见为止 lis[left] = lis[right] # 找见比tmp小的数,此时插入到左边空出的那个位置 while left < right and lis[left] <= tmp: # 从左边找比tmp大的数 left += 1 # 如果左边的数总比取出的数小,则往右前进一位继续找直到找见为止 lis[right] = lis[left] # 找见比tmp大的数,此时插入到右边空出的那个位置 lis[left] = tmp # 再把中间这个值tmp写回来 return left # 返回中间这个值,left,right最后重合在一起了
lis = [5, 7, 4, 6, 3, 1, 2, 9, 8] partition(lis, 0, len(lis) - 1) print(lis) # [2, 1, 4, 3, 5, 6, 7, 9, 8] # 可以看出5归位
以上是我们的基本思想,但是如果不从最左边取这个tmp,而是从中任意取一个数作为我们的tmp值呢?
代码:
import random def partition(li, left, right): i = random.randint(left, right) # 从中取一个随机数i li[left], li[i] = li[i], li[left] # 把它调换位置放在最左边 tmp = li[left] while left < right: while left < right and li[right] >= tmp: right -= 1 li[left] = li[right] while left < right and li[left] <= tmp: left += 1 li[right] = li[left] li[left] = tmp return left def quick_sort(lis, left, right): if left < right: mid = partition(lis, left, right) # 返回中间这个值 quick_sort(lis, left, mid - 1) # 对左边的进行排序 quick_sort(lis, mid + 1, right) # 对右边的进行排序 lis = list(range(10000)) random.shuffle(lis) quick_sort(lis, 0, len(lis) - 1) print(lis)
如果上面没有记住的话,ok可以看下面这种,这种快排方式代码更加简略和易懂,也更加pythonic
def quick_sort(lis): if len(lis) < 2: return lis else: pivot = lis[0] # 选定的基准值,总取左边第一个值 left = [i for i in lis[1:] if i <= pivot] # 小于等于基准值的元素组成的列表 right = [i for i in lis[1:] if i > pivot] # 大于基准值的元素组成的列表 return quick_sort(left) + [pivot] + quick_sort(right) lis = [9, 5, 2, 8, 6, 1, 4, 7, 3] print(quick_sort(lis)) # 把左边的数组+基准值+右边的数组 # 第一次基准值9 [5,2,8,6,1,4,7,3] + [9] + [] # 第二次基准值5 [2,1,4,3] + [5] + [8,6,7] + [9] + [] # 第三次基准值2 [1]+[2] + [4,3] + [5] + [8,6,7] + [9] + [] # 第四次基准值4 [1]+[2] + [3]+[4]+[] + [5] + [8,6,7] + [9] + [] # 第四次基准值8 [1]+[2] + [3]+[4]+[] + [5] + [6,7]+[8]+[] + [9] + [] # 第五次基准值6 [1]+[2]+[3]+[4]+[]+[5]+[]+[6]+[7] +[8] + [] + [9] + []
把上面代码一行实现
lis = [3, 6, 12, 21] quick_sort = lambda lis: lis if len(lis) < 2 else quick_sort( [i for i in lis[1:] if i <= lis[0]]) + [lis[0]] + quick_sort([i for i in lis[1:] if i > lis[0]]) print(quick_sort(lis))
3.2 堆排(最复杂的一个,利用二叉树)
3.2.1 二叉树相关概念
结点的度(Degree):一个结点拥有的子树数目称为该结点的度
二叉树:度不超过2的树(节点最多有两个叉)
深度(Depth):树中结点最大层次的值
满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。树的特点是每一层上的节点数都是最大节点数
完全二叉树:在一棵二叉树中,除最后一层外,若其余层都是满的,并且最后一层或者是满的,或者是在右边缺少连续若干节点,则此二叉树为完全二叉树
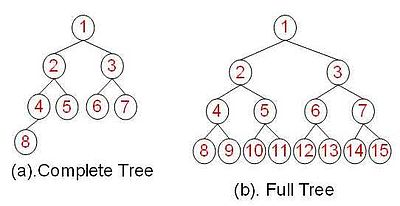
关于二叉树的存储方式:
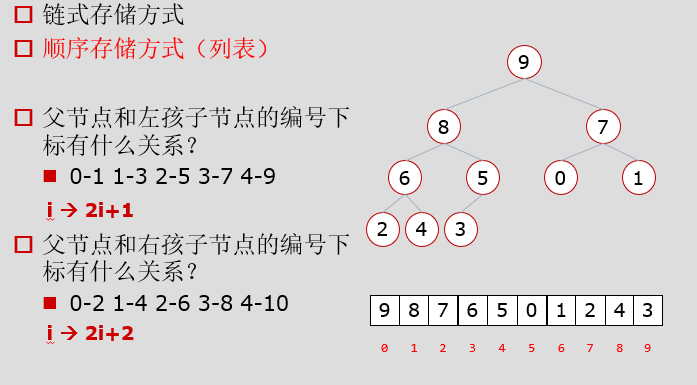
3.2.2 关于堆排序
堆分为最大堆和最小堆,其实就是完全二叉树
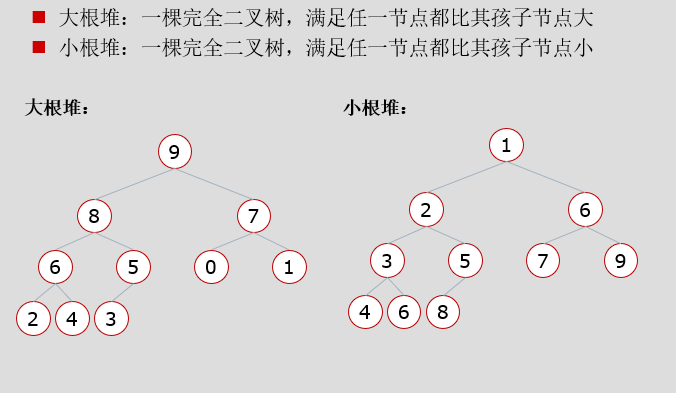
堆排序算法就是抓住了堆的特点,每次都取堆顶的元素,然后将剩余的元素重新调整为最大堆,依次类推,最终得到排序的序列。
堆排序过程:
1.建立堆
2.得到堆顶元素,为最大元素
3.去掉堆顶,将堆最后一个元素放到堆顶,此时可通过一次调整重新使堆有序
4.堆顶元素为第二大元素
5.重复步骤3,直到堆变空
这里我们要怎么建立堆呢???
堆排序的基本实现思路:
给定一个列表array=[6,8,1,9,3,0,7,2,4,5],对其进行堆排序
第一步:根据该数组元素构建一个完全二叉树
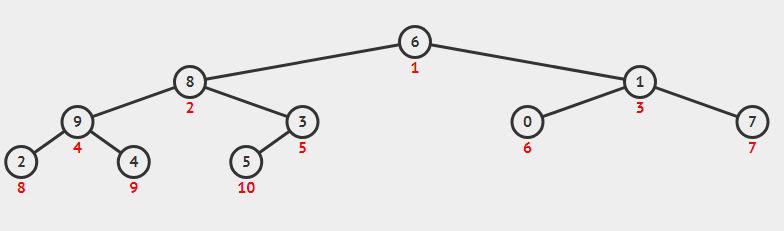
第二步:初始化构造(从最后一个有子节点开始往上调整最大堆)
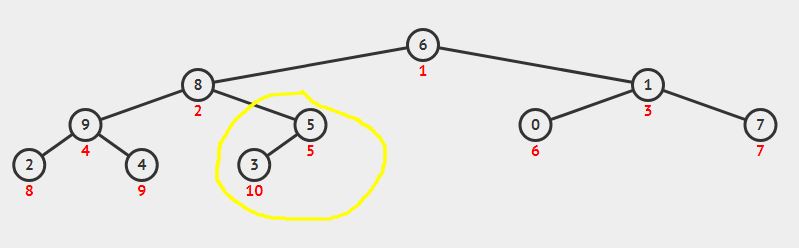
继续调整
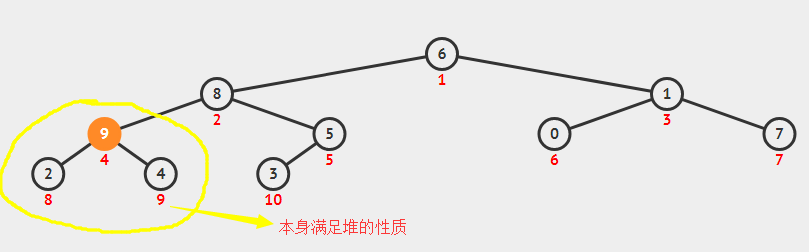
继续调整
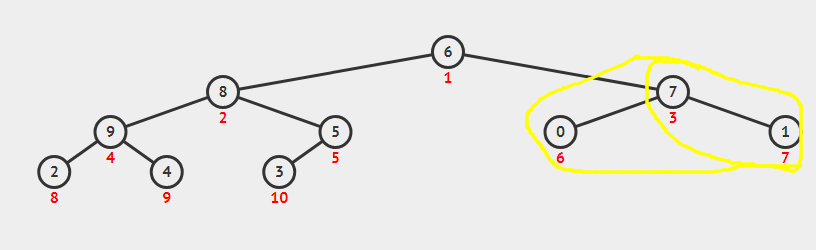
继续调整
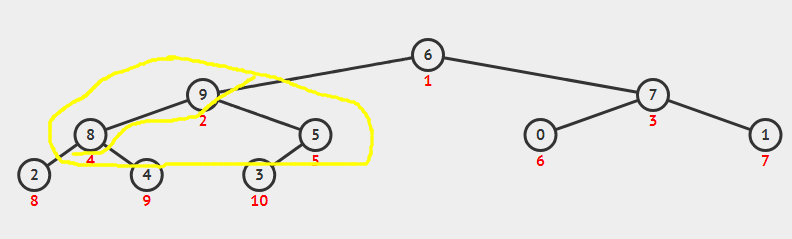
继续调整
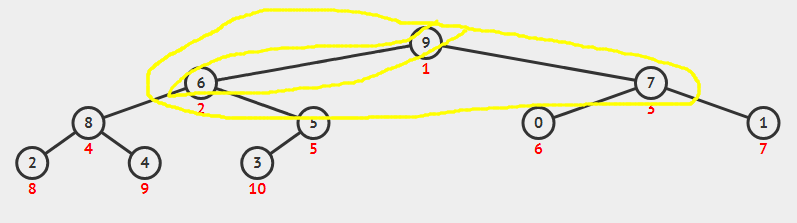
交换到这里的时候我们可以看到6和8其实还不满足堆的性质,所以还需要进行调整
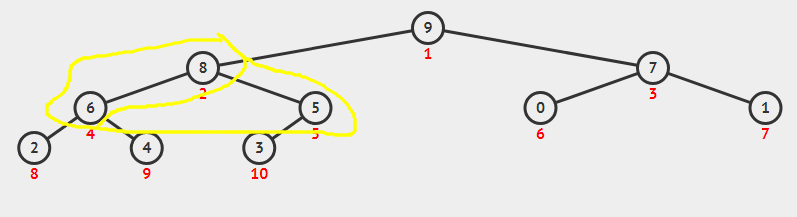
这样就得到了一个初始堆
我们构造好了堆,怎么一个出数呢???这里我们还要对它进行出数调整:
每次调整都是从父节点、左孩子节点、右孩子节点三者中选择最大者跟父节点进行交换
交换之后可能造成被交换的孩子节点不满足堆的性质,因此每次交换之后要重新对被交换的孩子节点进行调整
出数:
第一步:9出来,3上去

堆调整,让它满足堆的性质

第二步:8出来,3上去

堆调整,让它满足堆的性质
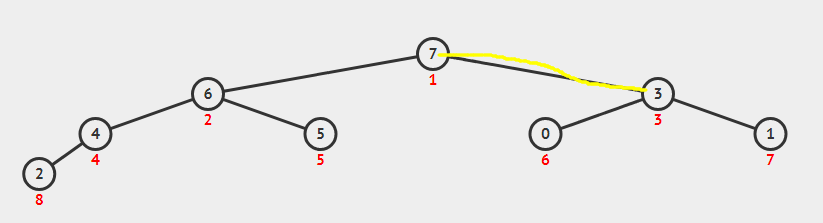
第三步:7出来,2上去
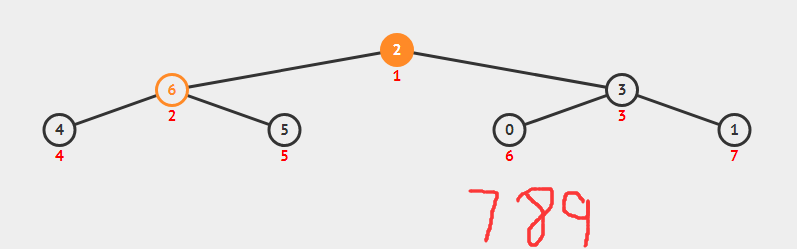
堆调整,让它满足堆的性质

第四步:6出来,1上去
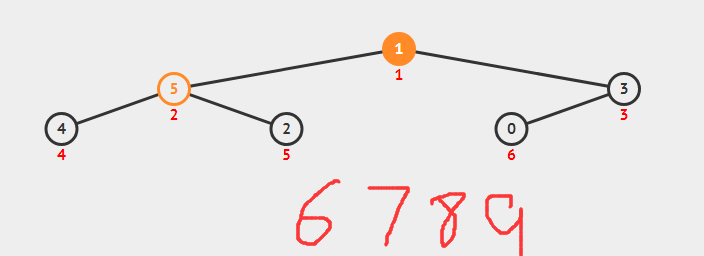
堆调整,让它满足堆的性质
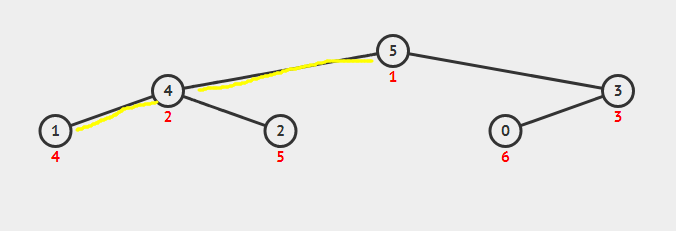
第五步:5出来,0上去
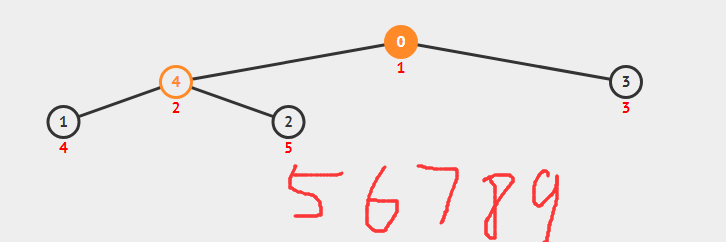
堆调整,让它满足堆的性质
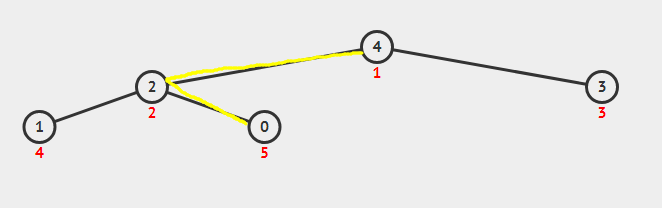
第六步:4出来,0上去

堆调整,让它满足堆的性质
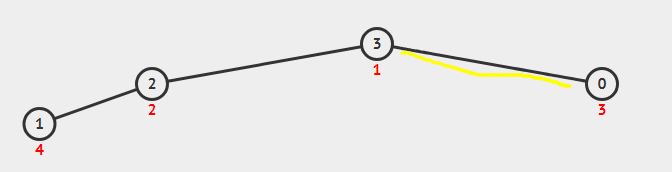
第七步:3出来,1上去
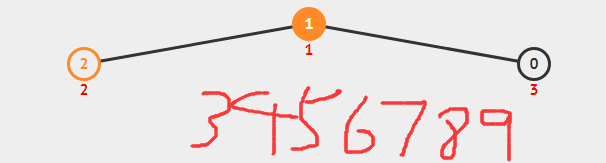
堆调整,让它满足堆的性质
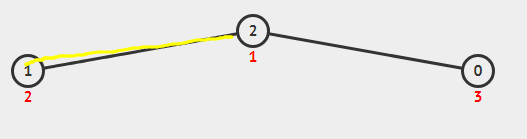
第八步:2出来,1上去

堆调整,让它满足堆的性质
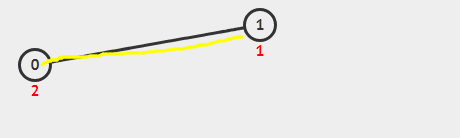
第九步:1出来,0上去
第十步:0出来

说明:
不管是初始大顶堆的从下往上调整,还是堆顶堆尾元素交换,每次调整都是从父节点、左孩子节点、右孩子节点三者中选择最大者跟父节点进行交换,交换之后都可能造成被交换的孩子节点不满足堆的性质,因此每次交换之后要重新对被交换的孩子节点进行调整。
以上逻辑已经有了,下来是编写代码:
# 调整堆,单独运行只能一次调整一下 def sift(lis, low, high): """ low是待调整的堆的根节点的位置索引 high是堆的最后节点的位置,用来判断是否越界 """ i = low # 当前的空位 j = 2 * i + 1 # 左边那个孩子 tmp = lis[i] # 出来的那个数 while j <= high: if j < high and lis[j + 1] > lis[j]: # 右孩子存在并且右孩子大于左孩子 j += 1 # j指向右孩子 if tmp < lis[j]: # 出来的数小于左边那个数 lis[i] = lis[j] # lis[j]应该上去 i = j # 再重新算 j = 2 * i + 1 else: # tmp比左边这个孩子大则不用动 break lis[i] = tmp # 堆排序 def heap_sort(li): # 先构造堆 n = len(li) for i in range(n//2,-1,-1): # i是调整子树的根,从n//2开始,一直到0 sift(li,i,n-1) # 整个堆的最后一个节点的位置当做high # 挨个出数 for i in range(n-1,-1,-1): # i是当前堆的最后一个元素位置 li[0],li[i] = li[i],li[0] sift(li,0,i-1) # 调整 li = [6,8,1,9,3,0,7,2,4,5] heap_sort(li) print(li)
可以看图
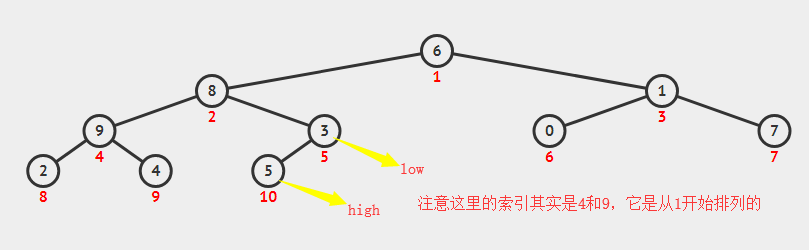
第二个版本,代码比较详细,可以作为参考:
def sift_down(array, start, end): """ 调整成大顶堆,初始堆时,从下往上;交换堆顶与堆尾后,从上往下调整 :param array: 列表的引用 :param start: 父结点 :param end: 结束的下标 :return: 无 """ while True: # 当列表第一个是以下标0开始,结点下标为i,左孩子则为2*i+1,右孩子下标则为2*i+2; # 若下标以1开始,左孩子则为2*i,右孩子则为2*i+1 left_child = 2 * start + 1 # 左孩子的结点下标 # 当结点的右孩子存在,且大于结点的左孩子时 if left_child > end: break if left_child + 1 <= end and array[left_child + 1] > array[left_child]: left_child += 1 if array[left_child] > array[start]: # 当左右孩子的最大值大于父结点时,则交换 temp = array[left_child] array[left_child] = array[start] array[start] = temp start = left_child # 交换之后以交换子结点为根的堆可能不是大顶堆,需重新调整 else: # 若父结点大于左右孩子,则退出循环 break def heap_sort(array): # 堆排序 # 初始化大顶堆 first = len(array) // 2 - 1 # 最后一个有孩子的节点(//表示取整的意思) for i in range(first, -1, -1): # 从最后一个有孩子的节点开始往上调整 sift_down(array, i, len(array) - 1) # 初始化大顶堆 # 交换堆顶与堆尾 for head_end in range(len(array) - 1, 0, -1): # start stop step array[head_end], array[0] = array[0], array[head_end] # 交换堆顶与堆尾 sift_down(array, 0, head_end - 1) # 堆长度减一(head_end-1),再从上往下调整成大顶堆 if __name__ == "__main__": array = [6, 8, 1, 9, 3, 0, 7, 2, 4, 5] heap_sort(array) print(array)
该代码参考来源链接:猛戳此处
以上说了这么多,能看懂已经很不错了,更何况还需要嘴啃。但是对于学Python的朋友来说,python内置模块heapq已经帮我们实现了堆排序,我们可以直接调用它实现一个堆排序
python内置模块heapq的简单使用:
import heapq x = [6, 8, 1, 9, 3, 0, 7, 2, 4, 5] heapq.heapify(x) print(x) # 一个堆排,默认小顶堆 # [0, 2, 1, 4, 3, 6, 7, 9, 8, 5] heapq.heappush(x, -1) # 添加一个值 print(x) # [-1, 0, 1, 4, 2, 6, 7, 9, 8, 5, 3] print(heapq.heappop(x)) # 取出堆顶元素 print(x) # -1 print(heapq.nsmallest(5, [1,5,4,7,2,8,9,3,0])) # 返回最小的5个元素 # [0, 1, 2, 3, 4] print(heapq.nlargest(5, [1,5,4,7,2,8,9,3,0])) # 返回最大的5个元素 # [9, 8, 7, 5, 4]
实现排序:
import heapq def heap_sort(li): heapq.heapify(li) # 先进行堆排序 res = [] for i in range(len(li)): res.append(heapq.heappop(li)) return res print(heap_sort([6, 8, 1, 9, 3, 0, 7, 2, 4, 5])) # [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
例题:
现有n个数,设计算法找出前k大的数(k<n)
思路:
1.取列表前k个元素建立一个小根堆。堆顶就是目前第k大的数。
2.依次向后遍历原列表,对于列表中的元素,如果小于堆顶,则忽略该元素;如果大于堆顶,则将堆顶更换为该元素,并且对堆进行一次调整。
3.遍历列表所有元素后,倒序弹出堆顶。

# 调整堆 def sift(lis, low, high): # low是待调整的堆的根节点的位置, # high是堆的最后节点的位置,用来判断是否越界 i = low # 当前的空位 j = 2 * i + 1 # 左边那个孩子 tmp = lis[i] # 出来的那个数 while j <= high: if j < high and lis[j + 1] > lis[j]: # 右孩子存在并且右孩子大于左孩子 j += 1 # j指向右孩子 if tmp < lis[j]: # 出来的数小于左边那个数 lis[i] = lis[j] # lis[j]应该上去 i = j # 再重新算 j = 2 * i + 1 else: # tmp比左边这个孩子大则不用动 break lis[i] = tmp def top(lis, k): heap = lis[0:k] # 取出k之前的数 for i in range(k // 2 - 1, -1, -1): # i是调整子树的根 sift(heap, i, k - 1) # 调整堆 for i in range(k, len(lis)): if lis[i] > heap[0]: heap[0] = lis[i] sift(heap, 0, i - 1) for i in range(k - 1, -1, -1): heap[0], heap[i] = heap[i], heap[0] sift(heap, 0, i - 1) lis = [6, 8, 1, 9, 3, 0, 7, 2, 4, 5] top(lis, 3)
3.3 归并排序 时间复杂度:O(nlogn) 空间复杂度:O(n)
将两段有序的列表合并成一个有序的列表

图解
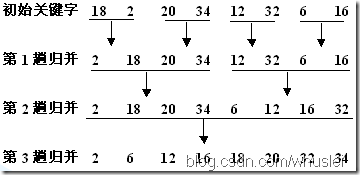
代码
# 两段有序排序 def merge(li, low, mid, high): i = low j = mid + 1 li_tmp = [] while i <= mid and j <= high: if li[i] <= li[j]: li_tmp.append(li[i]) i += 1 else: li_tmp.append(li[j]) j += 1 while i <= mid: li_tmp.append(li[i]) i += 1 while j <= high: li_tmp.append(li[j]) j += 1 li[low:high + 1] = li_tmp # li = [2,5,7,8,9,1,3,4] # merge(li,0,(len(li)-1)//2,len(li)-1) # print(li) # [2, 5, 7, 8, 9, 1, 3, 4] def _merge_sort(li, low, high): if low < high: # 至少有两个元素 mid = (low + high) // 2 _merge_sort(li, low, mid) _merge_sort(li, mid + 1, high) merge(li, low, mid, high) li = [2,5,7,8,9,1,3,4] _merge_sort(li, 0, len(li)-1) print(li)
3.5 以上算法说明
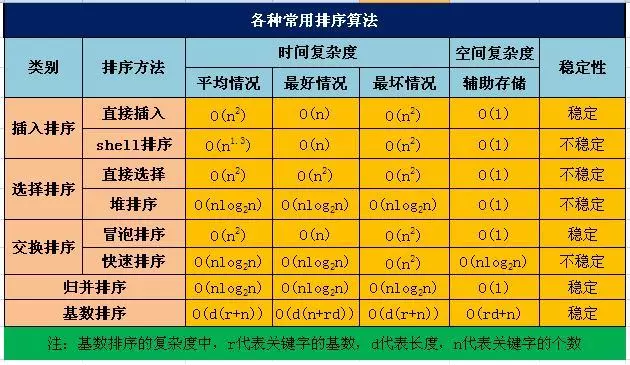
一般情况下,就运行时间而言:
快速排序 < 归并排序 < 堆排序
三种高级排序算法的缺点:
快速排序:极端情况下排序效率低
归并排序:需要额外的内存开销
堆排序:在快的排序算法中相对较慢
3.6 算法例题
有一个长度为 n 的数组 a,里面的元素都是整数,现有一个整数 b,写程序判断数组 a 中是否有两个元素的和等于 b?

def func(lis,d): count = [] for index,i in enumerate(lis): for j in lis[index+1:]: if i +j == d: count.append((i,j)) return count lis = [2,3,8,9,16,11] ret = func(lis,11) print(ret)
参考博客:https://www.jianshu.com/p/a33aa5cf7af1
官方演示效果参考图:猛戳此处
更多相关介绍可供参考:猛戳此处



 浙公网安备 33010602011771号
浙公网安备 33010602011771号