Python高级之递归函数
1.如何更好的学习Python2.Python准备之Python环境安装和Pycharm使用3.Python准备之笔记-MarkDown格式及云端笔记4.Python准备之软件开发规范5.Python基础之计算机基础6.Python基础之编程语言7.Python基础之Python基本构成8.Python基础之流程控制9.Python特殊机制之垃圾回收机制10.Python中级之数据类型的内置方法11.Python中级之可变数据类型和不可变数据类型12.Python中级之文件操作13.Python中级之列表字典推导式和三元运算符14.Python中级之深浅拷贝15.Python中级之字符编码16.Python中级之异常处理17.Python中级之解压赋值18.Python高级之闭包函数19.Python高级之函数介绍20.Python高级之名称空间与作用域21.Python高级之装饰器22.Python高级之模块与包23.Python高级之迭代器与生成器24.Python模块之re模块25.Python模块之os模块26.Python模块之random模块27.Python模块之序列化模块(json模块与pickle模块)28.Python模块之time模块和datetme模块
29.Python高级之递归函数
30.Python高级之常见的内置函数31.Python模块之sys模块32.Python模块之hashlib模块33.Python模块之logging模块34.Python面向对象之面向对象编程35.Python面向对象之三大特征-封装36.Python面向对象之绑定方法和非绑定方法37.Python面向对象之三大特征-继承38.Python面向对象之三大特征-多态39.Python面向对象之派生40.Python面向对象之组合41.Python面向对象之反射递归函数
【一】概要
- 递归函数是一种自我调用的函数,即在函数定义中直接或间接地调用函数本身。递归通常用于解决可以被分解为相似子问题的问题,使得问题的解决方法更加清晰和简洁。
【二】常见用法
- 基本情况(Base Case): 定义递归终止的条件,避免函数无限递归。在基本情况下,函数直接返回一个结果,而不再调用自身。
- 递归步骤: 在递归情况下,函数调用自身,但问题规模较小。通过逐步缩小问题规模,最终达到基本情况,从而得到最终的结果。
(1) 存在限制条件,当满足这个限制条件的时候,递归便不再继续。
(2) 每次递归调用之后越来越接近这个限制条件
def add(i): print(i) if i == 1: # 设置基本情况 return '回溯了' # 终止递归 return add(i - 1) print(add(5))
【三】详解
【1】递归
- 假设我们现在都不知道什么是递归,我们自然想到打开浏览器:输入到谷歌的网页,点击搜索递归,然后在为维基百科中了解到了递归的基本定义。在了解到了递归实际上是和栈有关的时候,你又蒙圈了,什么是栈呢?数据结构没学清楚,此时的你只能又打开谷歌,搜索什么是栈。接下来你依次了解了内存/操作系统。在你基本了解好知识之后,你通过操作系统了解了内存,通过内存了解了栈,通过栈了解了什么是递归这下你恍然大悟!原来这就是递归啊!
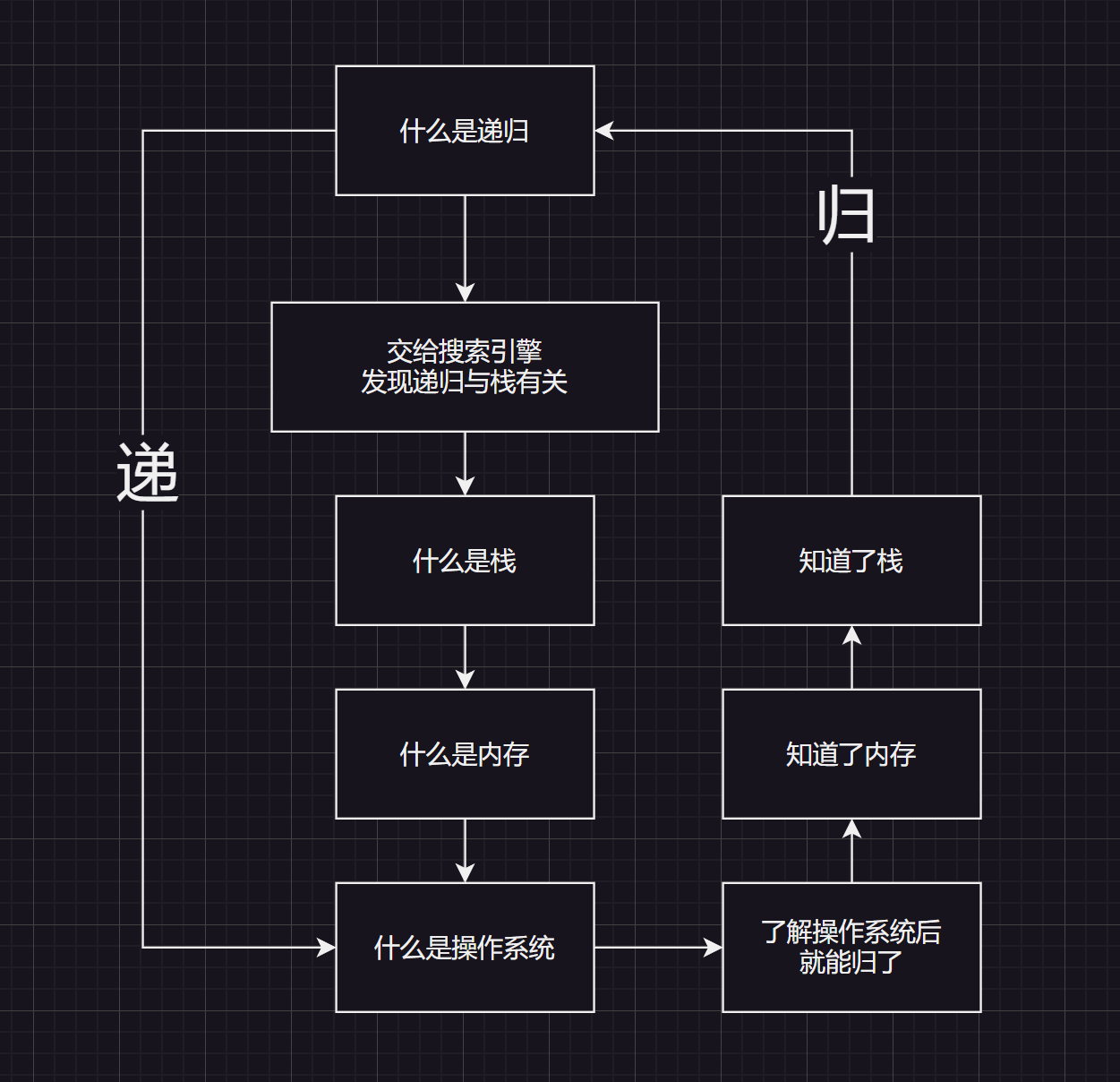
- 递归是需要终止条件的,那么你明白递归是什么其实就是终止条件。整个过程,搜索引擎充当递归函数(只是形象的假设)。在你去依次查找递归/栈/内存/操作系统的过程为前行阶段,在你都了解完之后,反回去了解含义的过程为退回阶段。
【2】递归的两大要素
第一要素:寻找递归结束条件
第二要素:每次递归调用之后越来越接近这个限制条件
【3】练习
以下是一些递归练习题,从简单到难:
- 计算阶乘: 编写一个递归函数,计算给定正整数
n的阶乘。- 斐波那契数列: 编写一个递归函数,计算斐波那契数列的第
n项。斐波那契数列的定义是:F(0) = 0, F(1) = 1, F(n) = F(n-1) + F(n-2)。- 反转字符串: 编写一个递归函数,将输入的字符串反转。例如,输入字符串 "hello",输出 "olleh"。
- 二进制搜索: 实现一个递归函数,在有序整数列表中执行二进制搜索。函数应该返回目标元素的索引,如果不存在,则返回 -1。
- 汉诺塔问题: 实现汉诺塔问题的递归解法。汉诺塔是一个经典问题,要求将一堆盘子从一个柱子移动到另一个柱子,其中大盘子不能放在小盘子上。
- 子集生成: 编写一个递归函数,生成给定集合的所有子集。
- 图的深度优先搜索(DFS): 实现图的深度优先搜索算法,以找到图中的所有节点。
- 归并排序: 实现归并排序算法,其中包括递归步骤。将一个列表分为两半,分别对两半进行排序,然后合并两个有序列表。
斐波那契数列
# 通过for循环创造斐波那契 a, b = 0, 1 # 斐波那契数列的第一位和第二位分别是0和1 time = int(input('需要查询多少位的斐波那契数列:>>>')) for i in range(0, time): a, b = b, a + b # 交换赋值 # a :前一轮的b # b :存储当前轮的a+b print(a, end=' ')
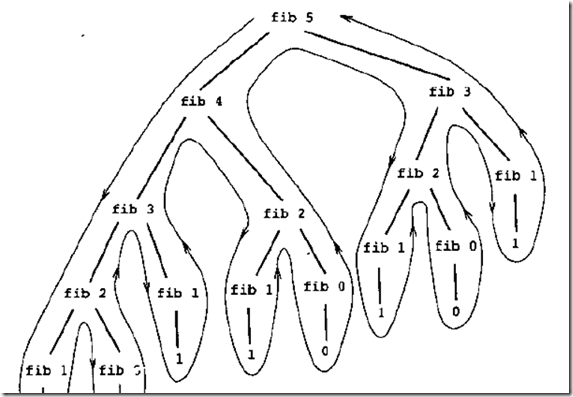
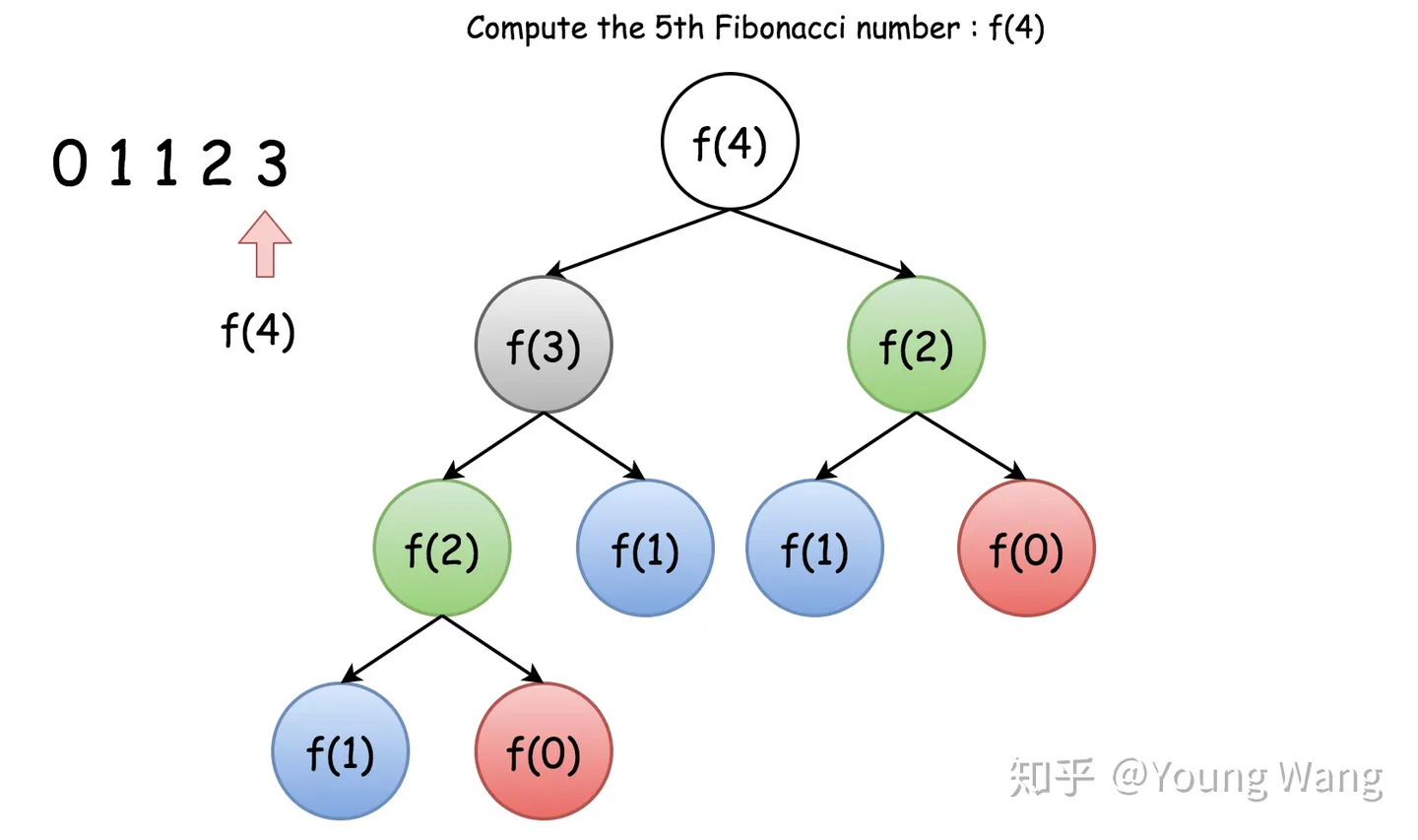
# 斐波那契数列 def fibonacci(n): # 递归基例 if n == 0: return 0 elif n == 1: return 1 # 递归步骤 else: return fibonacci(n - 1) + fibonacci(n - 2) print(fibonacci(5))
- 图示
- 箭头所示方向就是运行的顺序
阶乘
-
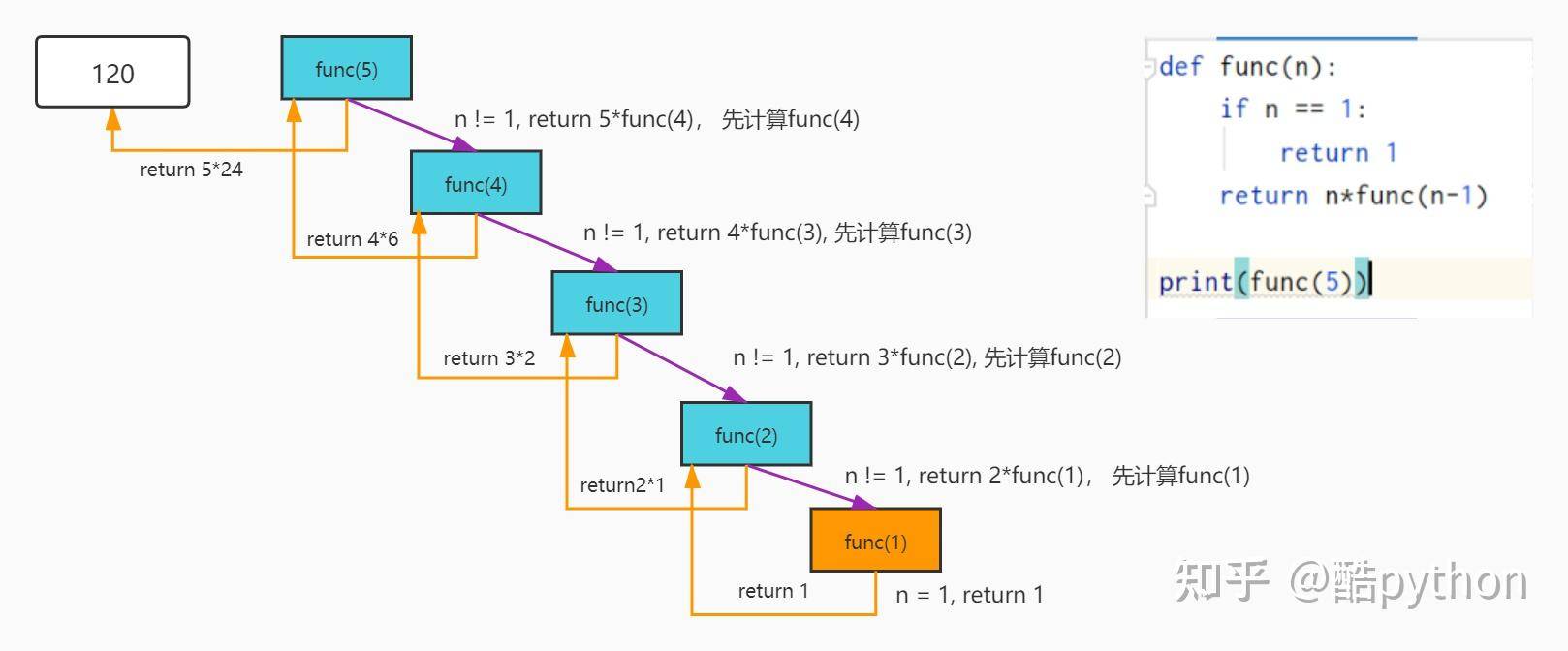
换一个角度来看
- func(1) 的返回结果是1,给了func(2)
- func(2) 计算2func(1) = 21 =2 , 将2作为结果返回给func(3)
- func(3) 计算3func(2) = 32 =6,将6返回给func(4)
- func(4) 计算4func(3) = 46=24, 将24返回给func(5)
- func(5) 计算5func(4) = 524=120,你最终得到的就是120
函数调用是一个过程,理解递归的关键是理解递归过程中的调用链是如何形成的,调用链的最后一个环节会有一个返回值,之后整个调用链条里的节点,都根据自己下一个节点的返回值计算自己的返回值并返回给上一个节点。最顶层的节点是你调用的,你得到的就是最终的结果。
def func(n): if n == 1: return 1 return n*func(n-1) print(func(5))
【4】递归的堆栈问题
递归函数可能引发堆栈溢出的问题,这是因为递归的本质是通过不断地调用自身来解决问题,而每一次递归调用都会在调用栈上增加一层。当递归深度过大时,可能导致调用栈的大小超过系统限制,从而触发堆栈溢出。
以下是处理递归函数堆栈问题的一些建议:
- 设定递归终止条件: 确保递归函数的终止条件能够在递归过程中得到满足。这样可以防止递归无限扩展,导致堆栈溢出。
- 合理设计递归深度: 在编写递归函数时,要注意递归深度的控制。尽量避免不必要的递归深度,考虑问题是否可以通过迭代或其他方式解决。
- 使用尾递归优化: 尾递归是一种特殊的递归形式,在函数的最后一步是递归调用的情况下,一些编译器和解释器可能对其进行优化,避免额外的调用栈增加。
- 使用迭代代替递归: 在某些情况下,可以通过迭代的方式替代递归,以避免调用栈的过度增长。
- 增大堆栈空间: 某些编程语言和环境允许配置堆栈大小。如果递归深度较大,可以尝试增大堆栈空间。
- 使用尾递归优化: 尾递归是一种特殊的递归形式,在函数的最后一步是递归调用的情况下,一些编译器和解释器可能对其进行优化,避免额外的调用栈增加。
- 避免过度递归: 在一些问题中,递归可能不是最优的解决方案。考虑是否存在其他更有效的算法,如动态规划等。
- 使用尾递归优化: 尾递归是一种特殊的递归形式,在函数的最后一步是递归调用的情况下,一些编译器和解释器可能对其进行优化,避免额外的调用栈增加。
学习递归的流程
- 理解递归的概念: 递归是一种通过调用自身来解决问题的方法。理解递归的核心思想是在解决一个大问题时,可以将其分解成一个或多个相似的子问题。
- 寻找递归的特征: 确定一个问题是否适合使用递归解决。通常,递归问题具有以下特征:
- 问题可以被分解成较小的同类问题。
- 解决问题的方式与解决其子问题的方式类似。
- 问题存在终止条件,可以在不再分解时直接求解。
- 学习递归的基本结构: 理解递归函数的基本结构,包括递归调用、递归终止条件等。典型的递归函数通常包含以下几个要素:
- 递归调用:在函数内部调用自身。
- 基本情况(递归终止条件):定义一个或多个终止递归的条件。
- 练习简单的递归问题: 从简单的问题开始,逐步提高难度。例如,计算阶乘、斐波那契数列、二叉树的遍历等问题都是递归问题的良好练习。
- 理解递归的调用栈: 递归调用是通过调用栈来实现的,理解递归函数在调用栈中的执行流程对于深入理解递归非常重要。
- 处理递归中的重复计算: 了解递归中可能存在的重复计算问题,并学会通过记忆化搜索或动态规划等方法进行优化。
- 解决更复杂的问题: 逐步挑战更复杂的递归问题,例如分治算法、图的深度优先搜索等。
- 参与实际项目和练习: 应用递归解决实际问题,参与算法竞赛,通过实践不断提升递归技能。
- 阅读他人的递归代码: 阅读其他人编写的递归代码,了解不同问题的递归实现方式,从中学到更多的技巧和经验。
- 持续学习: 递归是算法和编程中的一个重要主题,不断学习相关算法和数据结构的知识,拓展自己的递归应用领域。
总体而言,递归的学习是一个渐进的过程,需要通过理论学习、实践练习和参与项目等多方面的方式来提高自己的递归编程能力。




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 【.NET】调用本地 Deepseek 模型
· CSnakes vs Python.NET:高效嵌入与灵活互通的跨语言方案对比
· DeepSeek “源神”启动!「GitHub 热点速览」
· 我与微信审核的“相爱相杀”看个人小程序副业
· Plotly.NET 一个为 .NET 打造的强大开源交互式图表库