BUAA_OO_Unit1 总结
BUAA_OO_Unit1 总结
1 架构思路
1.1 作业概述
本单元作业的整体任务是对输入的函数表达式进行解析,返回一个化简后的表达式。其中函数表达式包括表达式、项、因子三个层次,而因子又包含幂因子、数字因子、三角因子、求和因子、自定义函数因子等种类。而化简的要求,则是最终表达式不含求和因子与自定义函数(即进行代入操作),且不含多余的未展开括号(即进行展开操作)。
1.2 整体思路
面对表达式化简的大任务,我们可以将其拆分为两个部分:表达式解析与表达式化简。其中表达式解析任务是将输入的字符串解析为具体的表达式类进行存储,针对此任务,作者采用课程组教授的递归下降解析方法,将字符串递归拆分成表达式-项-因子的递归向下结构进行存储;而针对表达式化简任务,作者采用了步骤分离+递归解析的整体方法,将化简过程分为了函数代入-表达式降幂-表达式展开-项内合并-项间合并五个步骤,每个步骤通过单独的类进行实现,且在类内也遵循了递归向下的解析方法。
1.3 设计优劣分析
整体架构的优势是解耦合度较高,实现了每一步的操作分离,易于定位bug的发生地,而且所有的方法均采用递归下降的思路,代码整体连贯易读,且对递归结构能够自然拆包解析;
架构的不足是在很多细节处还不能体现面向对象的思想,例如对于每一个化简步骤,由于我采用一种递归解析的方法,所以事实上每一个表达式层次都有对应的方法,即这是表达式类都要实现的公共方法,应该设计为接口更为合适。
2 程序结构度量
2.1 UML类图
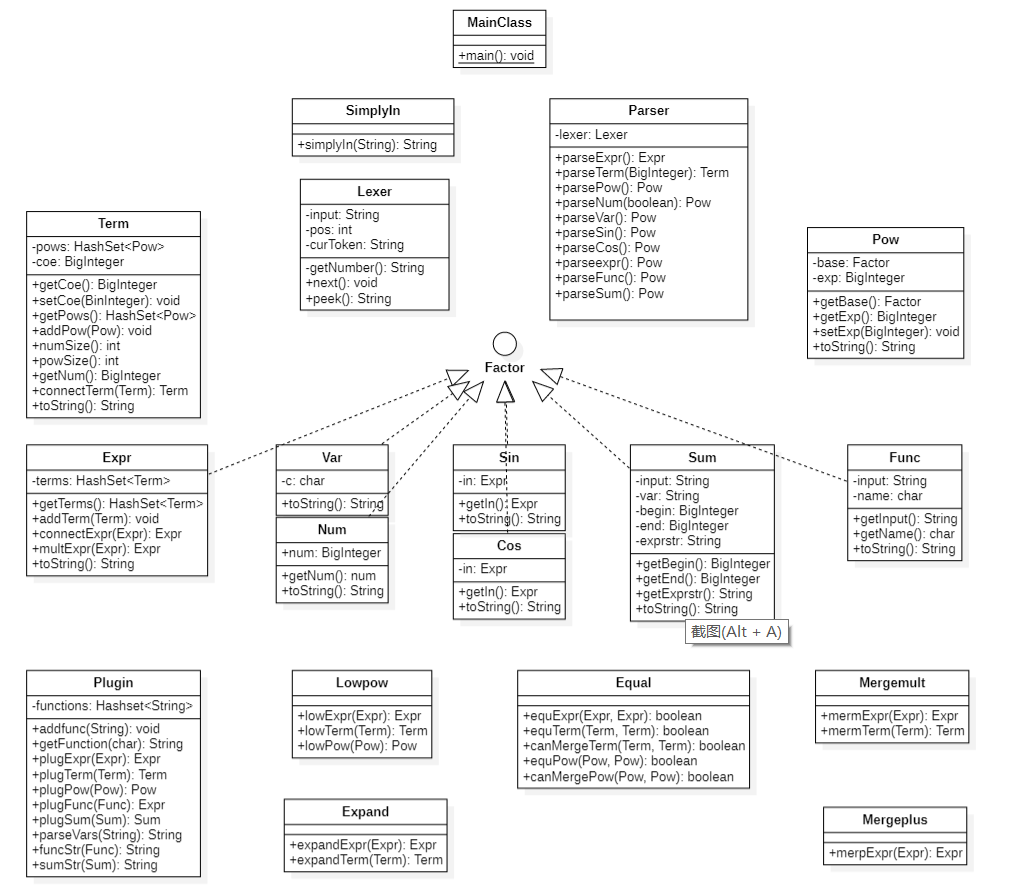
由类图可以更清楚地看出设计的整体思路:首先通过第一阶段的递归下降将输入的字符串解析成为层次化的表达式结构;之后通过第二阶段的五个步骤将表达式进行逐步解析。其中在合并过程中,我单独实现了Equal类对表达式的每一个层次进行比较,避免了重写equals方法容易出现bug的问题;此外,对于化简步骤本身的递归方法,我在处理类中实现,而别的方法我则在具体的表达式类中实现,从一定程度上避免了巨类的出现,整体代码结构比较平衡。
2.2 类方法度量
| method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| op.Plugin.parseVars(String) | 23.0 | 1.0 | 10.0 | 11.0 |
| op.Equal.equPow(Pow, Pow) | 14.0 | 6.0 | 11.0 | 14.0 |
| op.Equal.canMergeTerm(Term, Term) | 12.0 | 2.0 | 5.0 | 6.0 |
| op.Equal.equTerm(Term, Term) | 12.0 | 2.0 | 4.0 | 6.0 |
| op.Mergeplus.merpExpr(Expr) | 12.0 | 4.0 | 6.0 | 6.0 |
| readin.Parser.parsePow() | 12.0 | 8.0 | 11.0 | 11.0 |
| op.Equal.equExpr(Expr, Expr) | 11.0 | 2.0 | 4.0 | 5.0 |
| op.Plugin.funcStr(Func) | 11.0 | 1.0 | 10.0 | 10.0 |
| op.Equal.canMergePow(Pow, Pow) | 9.0 | 5.0 | 9.0 | 9.0 |
| op.Expand.expandTerm(Term) | 9.0 | 1.0 | 9.0 | 9.0 |
| op.Mergemult.mermTerm(Term) | 9.0 | 4.0 | 5.0 | 5.0 |
| expr.Expr.multExpr(Expr) | 8.0 | 3.0 | 5.0 | 5.0 |
| readin.Parser.parseExpr() | 7.0 | 1.0 | 7.0 | 7.0 |
| op.Lowpow.lowPow(Pow) | 6.0 | 1.0 | 5.0 | 5.0 |
| op.Plugin.plugPow(Pow) | 6.0 | 6.0 | 6.0 | 6.0 |
| expr.Cos.toString() | 5.0 | 3.0 | 2.0 | 3.0 |
| expr.Expr.toString() | 5.0 | 1.0 | 4.0 | 4.0 |
| ... | ... | ... | ... | ... |
| op.Plugin.plugFunc(Func) | 0.0 | 1.0 | 1.0 | 1.0 |
| op.Plugin.plugSum(Sum) | 0.0 | 1.0 | 1.0 | 1.0 |
| readin.Lexer.Lexer(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| readin.Lexer.peek() | 0.0 | 1.0 | 1.0 | 1.0 |
| readin.Parser.Parser(Lexer) | 0.0 | 1.0 | 1.0 | 1.0 |
| readin.SimplyIn.simplyIn(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| Total | 244.0 | 127.0 | 219.0 | 240.0 |
| Average | 2.90 | 1.51 | 2.61 | 2.86 |
从类方法度量的角度看,这份代码的整体复杂度还算适中,但是在一些方法中出现了复杂度过高的现象,这种现象主要源自于两个原因——①代码面向过程痕迹严重:例如parseVars方法,是利用括号匹配的规则对自定义函数进行因子的提取,而事实证明这种面向对象的代码也容易出bug;②使用过多分支语句:由于我几乎所有表达式类均实现了Factor接口,所以在因子层面往往需要利用许多分支语句对具体操作进行分类,使得分支变多,方法整体也较为臃肿。但是从另一方面说,正是由于我对处理的每一个步骤都实现了单独的类,所以整体的耦合性低,整体复杂度还是较低的。
3 bug分析与测试
3.1 出现的bug
本单元的作业出现的bug主要有:第二次作业在递归解析时返回了错误的对象(例如应该返回数字对象却返回幂对象);第三次作业出现的大整数问题;第三次作业出现的括号匹配问题;第三次作业出现的输出格式错误问题。
对问题进行回溯,可以很清楚的看出,错误代码正是出现在①代码分支较多处,导致返回对象混淆;②面向过程的复杂代码处,导致考虑问题步骤。所以可以看出代码复杂度与bug出现的难易度确实呈现一定程度上的正相关关系,在初步设计是就应该注意控制代码复杂度。
3.2 分析bug策略
分析bug主要策略有三:一是针对每次作业的增量开发部分进行定点测试,分析是否实现了功能的增量,例如函数嵌套等;二是测试边界数据,例如大整数数据,边界次幂数据等;第三则是利用自动评测数据(这里感谢hxy同学提供的自动测试程序帮我测出了程序的许多问题),对有问题数据进行简化与问题定位。
4 心得体会
- 好架构的重要性:在第一次作业的过程中,由于没有进行整体设计,所以我对自己的代码熟悉度不是很高,这直接导致了我第二次作业的重构;而第二次作业的整体设计和未来增量设想,反而为我第三次作业代码的编写提供了便利,这种对比让我确定了好架构的优势。
- 面向对象思想初探:回过头来看我的代码结构,不能说不好,但是也不能说完全符合面向对象要求,例如前文多次强调的实现接口问题。但是在设计过程中,我确实尝试采用荣文戈老师所说:“假设你有很多程序员,将任务分出去”的想法,这样的想法带给我的好处就是任务分得清,降低了整体代码的耦合度,这确实降低了我debug的难度。
- 学习是一个合作的过程:在开发过程中,我针对题目具体要求和同学进行了反复讨论,针对一些具体的技术问题也对同学进行了讨教,更别说从同学处获得了自动测试的程序,这些都使我的开发变得更为容易和清晰,可以体会到合作在代码开发过程中的重要性。




