统计学习——逻辑回归

  逻辑回归（logistic regression）是统计学习中的经典分类方法，它可以处理二元分类以及多元分类。虽然名字里有”回归“两字，那么这两者又有什么关系呢？

1.从线性回归到逻辑回归

  逻辑回归的原理是用逻辑函数将线性回归的结果\((-\infty,+\infty)\)映射到\((0,1)\)，故先介绍线性回归函数和逻辑函数。

1.1线性回归函数

  线性回归的模型是求出输出特征向量\(Y\)和输入样本矩阵\(X\)之间的线性关系系数\(\theta\)，满足\(Y=X\theta\)，即

\[Y = \theta_0 + \theta_1 x_1+···+\theta_nx_n = \theta^TX \]

  此时\(Y\)是连续的，属于回归模型。

1.2二元逻辑回归模型

  我们对线性回归的结果做一个函数\(g\)上的转换，可以变化为逻辑回归，这个\(g\)函数我们一般取为\(sigmoid\)函数，即

\[g(z) = \frac{1}{1+e^{-z}} \]

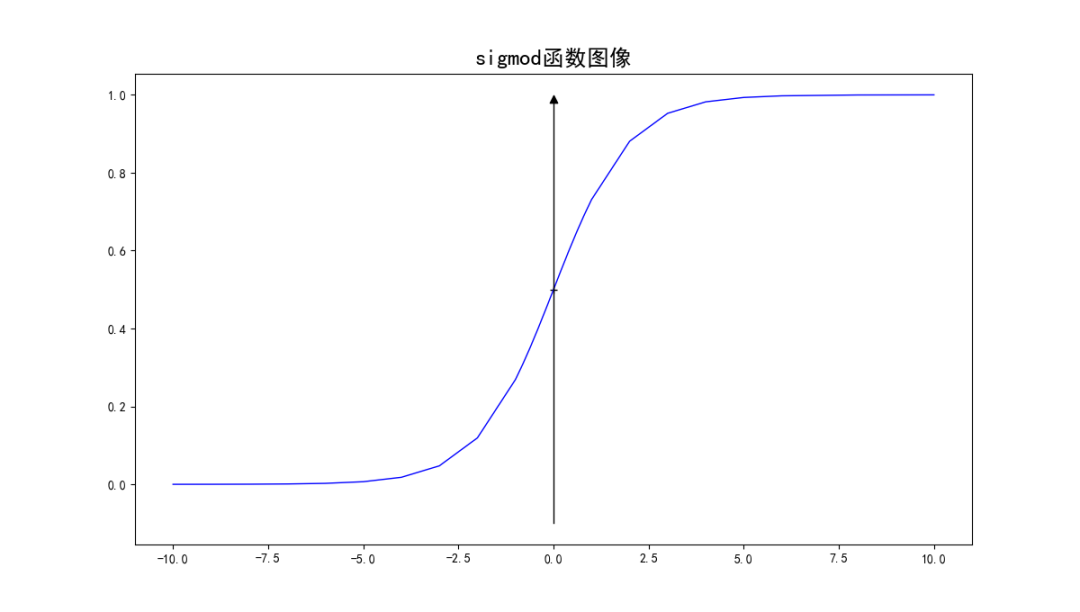
  从图中可以看出，当\(z\)趋于正无穷时，\(g(z)\)趋于\(1\)，而当\(z\)趋于负无穷时，\(g(z)\)趋于0，这就非常适合于分类概率模型。另外它还有一个导数性质：

\[g'(z) = g(z) (1-g(z)) \]

  如果我们令\(z=x\theta\)，这样就得到了二元逻辑回归模型的一般形式：

\[h(x )=\frac{1}{1+e^{-x\theta}} \]

  其中\(x\)为样本输入，\(h(x)\)为模型输出，可以看作是某一分类的概率大小。\(\theta\)为分类模型的要求的模型参数。对于二元样本来说，如果\(h(x) >0.5\)，即\(x\theta>0\)，则\(y=1\)。如果\(h(x) <0.5\)，即\(x\theta<0\)，则\(y=0\)。\(y=0.5\)是临界情况。

  \(h(x)\)的值越小，分类为\(0\)的概率越高，反之，值越大的话分类为\(1\)的概率就越高。如果靠近临界点，则分类准确率会下降。

  模型的损失函数目标是极小化损失函数来得到对应的模型参数\(\theta\)。

2.二元逻辑回归的损失函数

  我们用最大似然法来推导出我们的损失函数。

  按照二元逻辑回归的定义，假设我们的样本输出是0或者1两类。有：

\[\begin{aligned} P(y&=1|x) = h(x)\\ P(y&=0|x) = 1-h(x) \end{aligned} \]

  上面两个式子可以简写成一个式子，即：

\[P(y|x) = h(x)^y(1-h(x))^{1-y} \]

  \(y\)取0或1

  得到了\(y\)的概率分布函数表达式，我们就可以用极大似然函数法来求解模型参数\(\theta\)。

  似然函数为：

\[L(\theta) = \prod_{i=1}^m h(x^{(i)},\theta)^{y^{(i)}}(1-h(x,\theta))^{1-y^{(i)}} \]

  其中，\(m\)为样本个数。

  对似然函数对数化并取反可得到损失函数：

\[J(\theta) = -lnL(\theta) = -\sum_{i=1}^m[y^{(i)}~log(h(x^{(i)},\theta))+(1-y^{(i)})~log(1-h(x^{(i)},\theta))] \]

3.二元逻辑回归的损失函数的优化策略

  对于二元逻辑回归的损失函数最小化，常见的有梯度下降法，坐标轴下降法，拟牛顿法，这里我只给出有关梯度下降法的代数推
导，具体参考4. 二元逻辑回归的损失函数的优化方法

4.二元逻辑回归的正则化

  逻辑回归也会面临过拟合，我们可以使用正则化来避免过拟合。

  在经验风险最小化的基础上，尽可能采用简单的模型，可以有效提高泛化预测精度。如果模型过于复杂，变量值稍微有点变动，就会引起预测精度问题。正则化之所以有效，就是因为其降低了特征的权重，使得模型更为简单。

  正则化一般会采用\(L1\)范式或者\(L2\)范式。

  逻辑回归的\(L1\)正则化的损失函数表达式如下，相比普通的逻辑回归损失函数，增加了\(L1\)的范数做作为惩罚，超参数\(α\)作为惩罚系数，调节惩罚项的大小。

  二元逻辑回归的\(L1\)正则化损失函数表达式如下：

\[J(\theta) = -Y^T \circ log(h(\theta,X)) - (1-Y)^T \circ log (1-h(\theta,X)) +\alpha ||\theta||_1 \]

  \(\circ\)代表矩阵哈达玛积，逻辑回归的\(L1\)正则化损失函数的优化方法常用的有坐标轴下降法和最小角回归法。

  二元逻辑回归的L2正则化损失函数表达式如下：

\[J(\theta) = -Y^T \circ log (h(\theta,X)) - (1-Y)^T \circ log(1-h(\theta,X)) + \frac{1}{2} \alpha|| \theta||_2^2 \]

  逻辑回归的L2正则化损失函数的优化方法和普通的逻辑回归类似。