一个组合问题之拿球
给 \(n\) 个黑球,\(m\) 个白球,连续取直到不同色,将不同色的放回,求最后取到白球的概率 \(d_{n,m}\).
显然状态要多一个参数 \(k\) 才好转移,其中 \(\begin{aligned} d_{i,j,0} &= \frac{i}{i+j}d_{i-1,j,1} + \frac{j}{i+j}d_{i,j-1,2} \\ d_{i,j,1} &= \frac{j}{i+j}d_{i,j,0} + \frac{i}{i+j}d_{i-1,j,1} \\ d_{i,j,2} &= \frac{i}{i+j}d_{i,j,0} + \frac{j}{i+j}d_{i,j-1,2}\end{aligned}.\) 并不会优化,打表找规律.
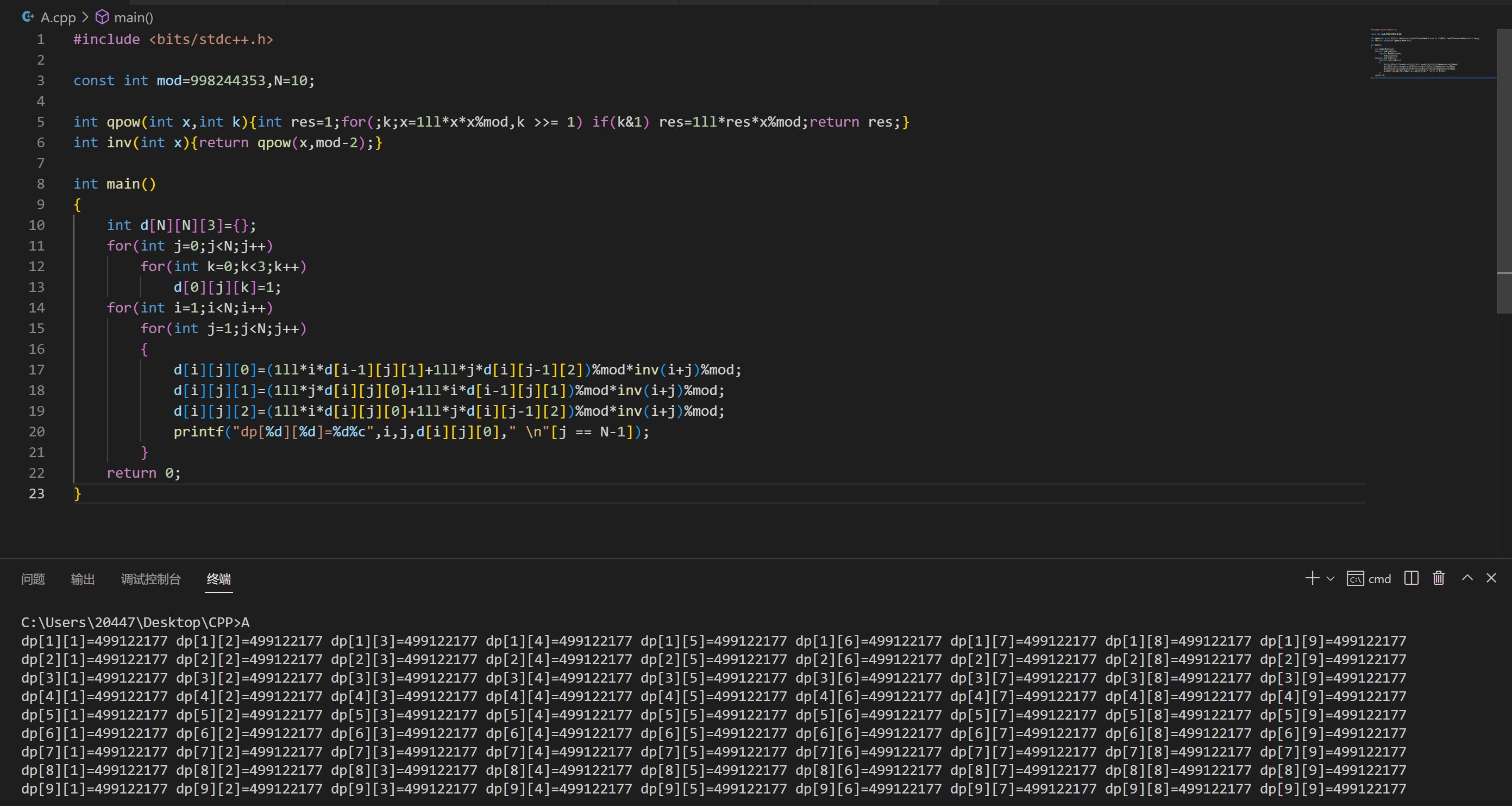
那么 \(d_{i,j}\) 就是 \(\frac{1}{2}\),用频率估计概率的方式我们可以 \(\Theta(T(n+m))\) 转转盘验证.
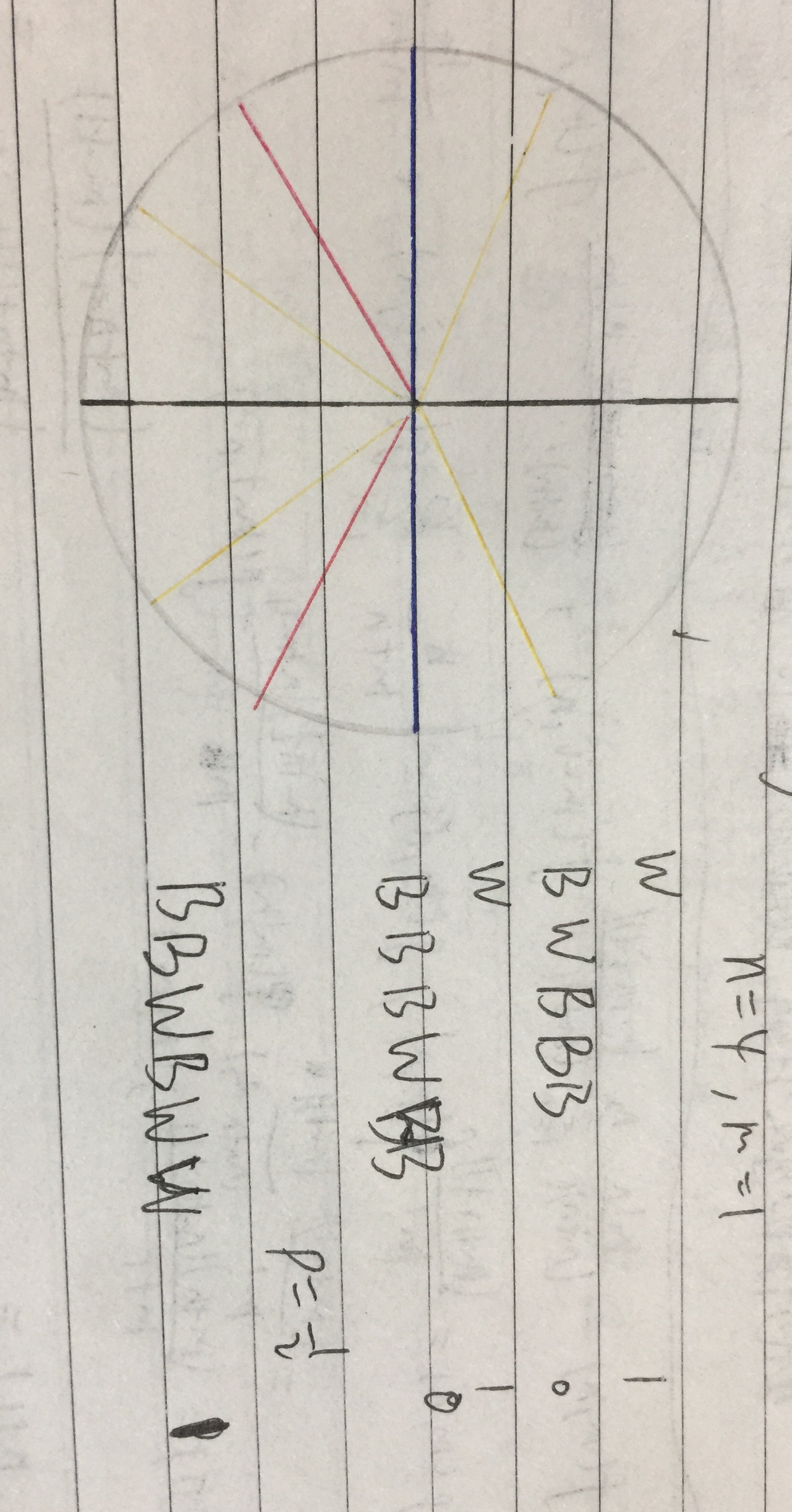
(迫真)
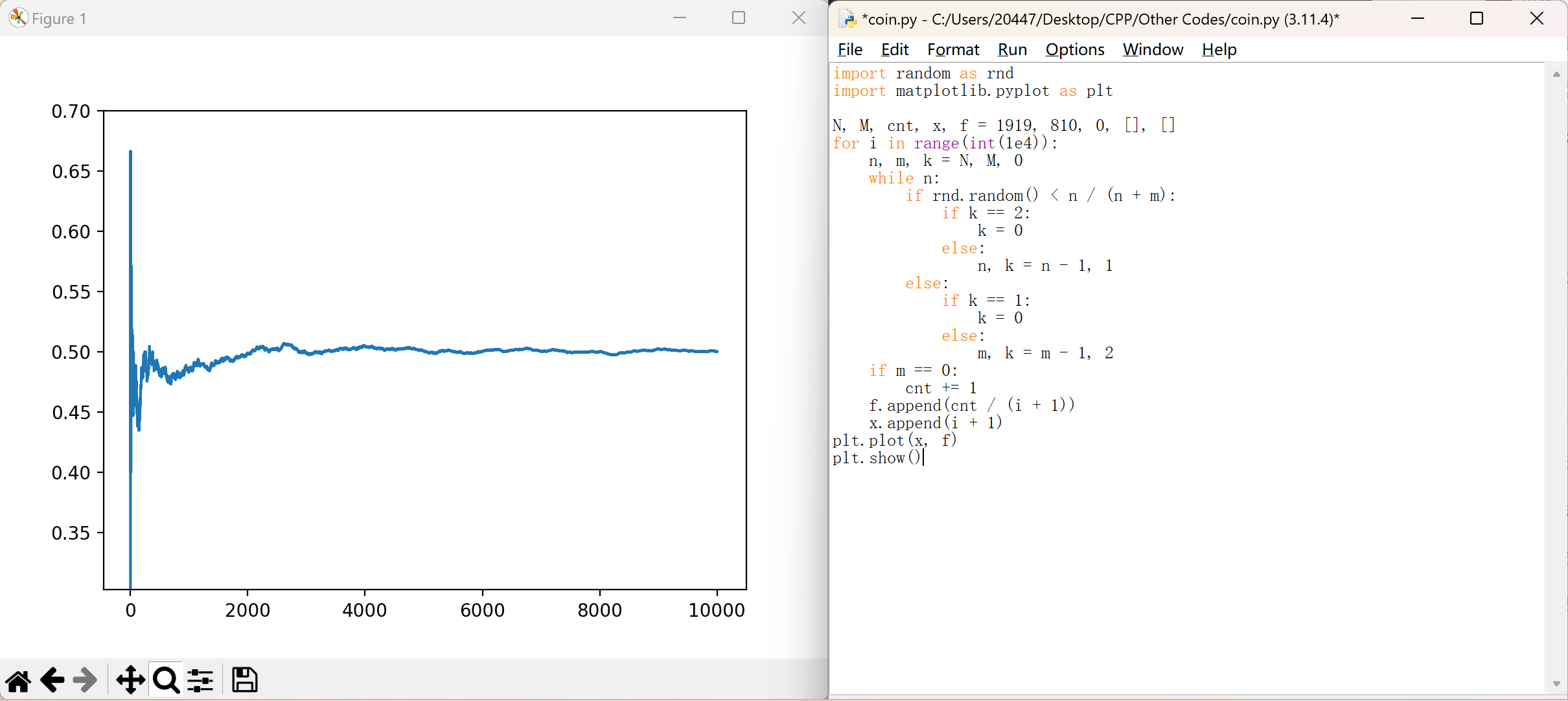
然后就只要归纳法证明楽.
\(\begin{aligned}d_{i,j,1} &= \frac{j}{i+j}\times\frac{1}{2} + \frac{i}{i+j}d_{i-1,j,1} \\ d_{i,j,1}-\frac{1}{2} &= \frac{i}{i+j}(d_{i-1,j,1}-\frac{1}{2}) \\ d_{i,j,1} &= \frac{1}{2}(1+\frac{1}{\binom{i+j}{i}}).\end{aligned}\)
同理 \(\begin{aligned}d_{i,j,2} = \frac{1}{2}(1-\frac{1}{\binom{i+j}{j}}).\end{aligned}\)
所以就有 \(d_{n,m}=\frac{n}{n+m}d_{n-1,m,1}+\frac{m}{n+m}d_{n,m-1,2} = \frac{1}{2}(1+\frac{n}{n+m}\frac{1}{\binom{n+m-1}{n-1}}-\frac{m}{n+m}\frac{1}{\binom{n+m-1}{m-1}}) = \frac{1}{2}\).
接下来考虑不借助 \(k\) 直接转移,为此需要规定连续取的个数 \(i\) 对贡献求和.
根据超几何分布,连续取 \(i\) 个黑球再取到白球的概率是 \(\frac{\binom{n}{i}}{\binom{n+m}{i}}·\frac{m}{n+m-i}.\)
白球同理,所以有 \(\begin{aligned}d_{n,m} = \sum^n_{i=1}\frac{\binom{n}{i}}{\binom{n+m}{i}}·\frac{m}{n+m-i}d_{n-i,m}+\sum^m_{i=1}\frac{\binom{m}{i}}{\binom{n+m}{i}}·\frac{n}{n+m-i}d_{n,m-i} .(*)\end{aligned}\)
归纳假设得到 \(\begin{aligned}d_{n,m} = \frac{1}{2}(\sum^{n-1}_{i=1}\frac{\binom{n}{i}}{\binom{n+m}{i}}·\frac{m}{n+m-i}+\sum^{m-1}_{i=1}\frac{\binom{m}{i}}{\binom{n+m}{i}}·\frac{n}{n+m-i})+\frac{1}{\binom{n+m}{n}}\end{aligned}.\)
利用对称性则有 \(d_{m,n} = d_{n,m} + \frac{1}{\binom{n+m}{m}} - \frac{1}{\binom{n+m}{n}} = d_{n,m} = \frac{1}{2}.\)
但是能否直接算呢?令 \(D_{n,m} = \frac{1}{n+m}\binom{n+m}{n}d_{n,m},\) 由 \((*)\), \(\begin{aligned} D_{n,m} = \frac{m}{n+m}\sum^n_{i=1}D_{n-i,m}+\frac{n}{n+m}\sum^m_{i=1}D_{n,m-i}.\end{aligned}\)
\(\begin{aligned}根据归纳假设,\ 2(n+m)D_{n,m} &= \sum^{n-1}_{i=1}\binom{n+m-i}{n-i}+\binom{m}{0} + \binom{n}{0}+\sum^{m-1}_{i=1}\binom{n+m-i}{m-i} \\ &= \sum^{n-1}_{i=0}\binom{m-1+i}{i}+\sum^{m-1}_{i=1}\binom{n-1+i}{i} \\ &= \binom{m+n-1}{m-1}+\binom{m+n-1}{n-1} \\ &= \binom{n+m}n{}.\end{aligned}\)
先说到这吧. 这道题来自北京大学去年概率论期末考试.
但是,为啥那么巧就是 \(\frac{1}{2}\) 呢?/kel
让我们观察 \(n=1919,m=810\) 的一个 case.
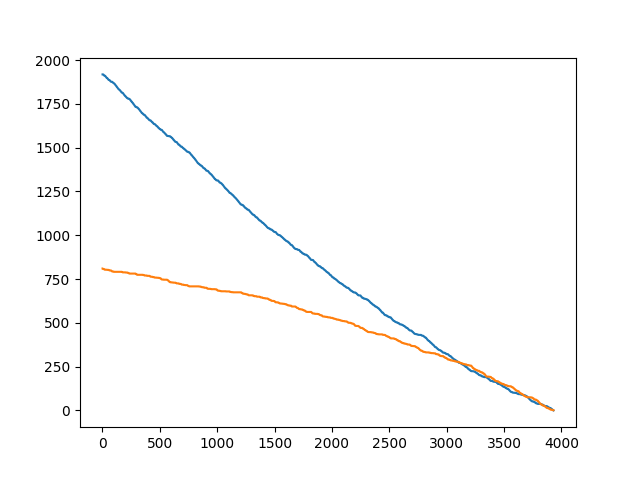
可以发现,因为当 \(n\) 大于 \(m\) 的时候迅速变到与 \(m\) 相同从而概率总是相同的,我把这样的转移称之为具有绝对优势.
所以,可以预测的,如果把题目改为取到不同色的不但将不同色放回,还要再放入一个不同色的球,那也是具有绝对优势的.
跑一组看看.
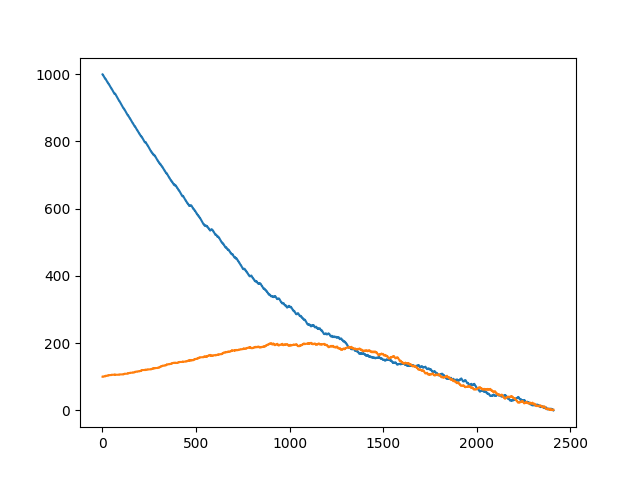
跑多组 \(n=1000,m=100\).
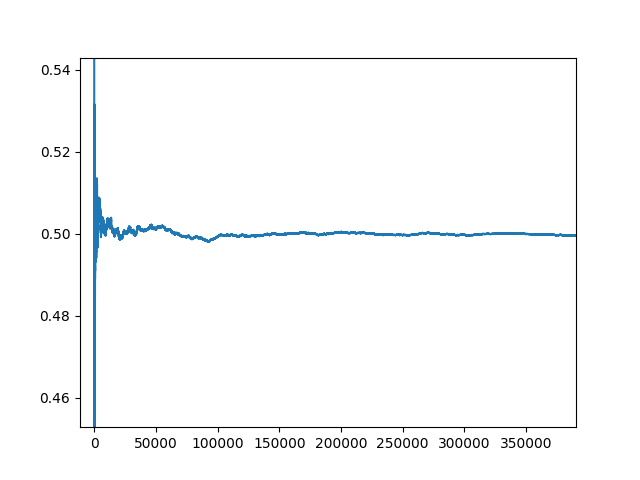
很对啊!
那样我们不妨推广一下,三种球的情形是否具有绝对优势呢?
观察 \(n_1 = 300, n_2 = 100, n_3 = 30\) 先被取完的 case.
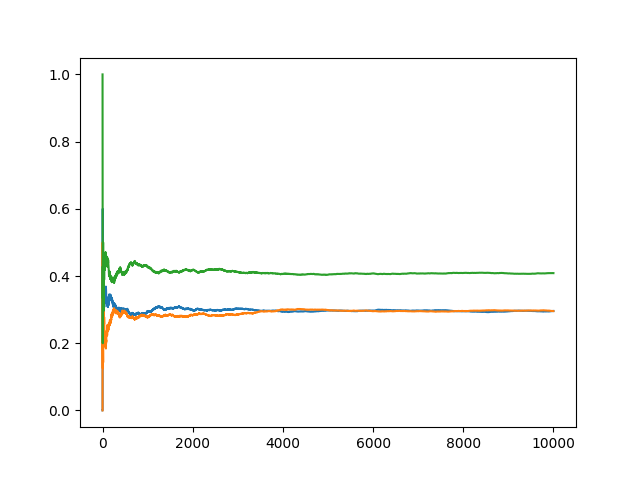
谔谔. 猜猜绿线是哪条的频率(如果你猜不出来我告诉你是 \(d_3\)),但似乎有 \(d_1 = d_2\).
可以推广最开始的式子打个表. 发现它不具有绝对优势.
但当我们改为取到不同色的不但将不同色放回,还要再放入一个不同色的球时,结果如下:
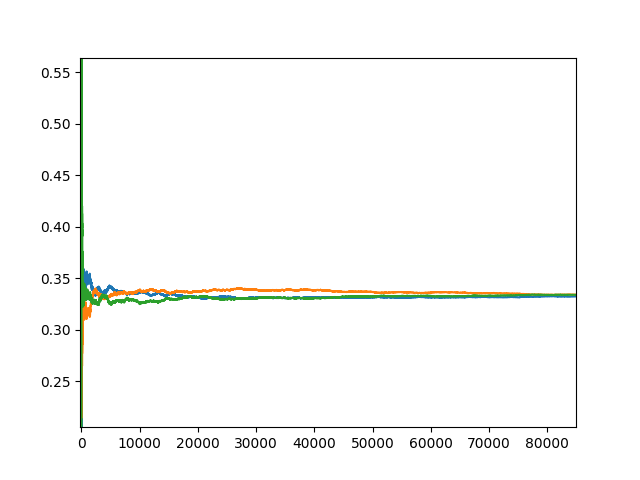
证明,推广和勘误可能会在明年给出(.
悲报:16746 41437 41817(放一拿一,{a_i}={1,1e4,1e4})

