江苏数学夏令营 2023
初等数论
\(1.\) (高联 2009 T3) 证明: 对每对正整数 \(k, l\), 有无穷多个 \(m\), 使得 \((C^k_m, l) = 1.\)
证明
令 $m = alk!+k, \ a \in \mathbb{Z_+},$ 则 $ C^k_m = (\frac{ak!}{k}l+1)(\frac{ak!}{k-1}l+1)\cdots(\frac{ak!}{1}l+1)$ 因为 $(dl+1,l) = (1, l) = 1, \ d \in \mathbb{Z},$ 可得 $(C^k_m, l) = 1.$\(2.\) (高联 2010 T2) 设 \(f^{(0)}(x) = x, \ f^{(1)}(x) = x\lceil x \rceil, \ f^{(l+1)}(x) = f(f^{(l)}(x)),\)
证明:如果 \(r = k + \frac{1}{2}, \ k \in \mathbb{Z_{\neq 0}}\), 则存在 \(m\), 使得 \(f^{(m)}(r) \in \mathbb{Z}\).
证明
设 $r = 2^tb + \frac{1}{2}, \ 2 \nmid b,$ 则 $f(r) = (2^tb+\frac{1}{2})(2^tb+1) = 2^{t-1}b(2^{t+1}b + 3) + \frac{1}{2},$ 则如果 $r = 2^tb + \frac{1}{2}, \ 2 \nmid b, $ 存在 $m$, 使得 $f^{(m)}(r) \in \mathbb{Z},$ 那么 $r = 2^{(t+1)}b + \frac{1}{2}, \ 2 \nmid b, f^{(m+1)}(r) \in \mathbb{Z}.$ 又当 $r = (2l + 1) + \frac{1}{2}, l \in \mathbb{Z}$ 时,$f(r) = k(k+1)+(l+1) \in \mathbb{Z},$ 原命题得证.\(3.\) (高联 2012 T2 推广) 给定 \(a\) 为大于 \(1\) 的正整数, \(p\) 为素数, 那么存在正整数 \(b\), 使得 \(b < pa − 1\) 且
\(pa \mid b(b + 1)\) 的充分必要条件是 \(a\) 不是 \(p\) 的幂.
必要性
若 $a$ 是 $p$ 的幂,即 $a = p^k, \ k \geq 1$, 命题转变为 $0 < b < p^{k+1}-1,\ p^{k+1} \mid b(b+1).$ 由 $(b, b+1) = (b, 1) = 1,$ 得 $p^{k+1} \mid b$ 或 $p^{k+1} \mid b+1,$ 与 $0 < b < p^{k+1}-1$ 显然矛盾.充分性
令 $a = p^ks, \ p \nmid s$, 则 $\exists i \in [1,s-1], \ (p^{k+1}i+1) \mid s$, 令 $b = p^{k+1}i$ 则满足条件.\(4.\) (高联 2011 T2) 设正整数 \(n \geq 4\), 证明: 存在多项式 \(f(x)\) 满足条件:
\((1) f(x) = x^n + a_{n-1}x^{n-1} + \cdots a_1x + a_0,\) 其中 \(a_i\) 均为正整数;
\((2)\) 对每个整数 \(m\) 以及任意 \(k \geq 2\) 个整数 \(r_i\), 均有 \(f(m) \neq \prod^k_{i=1} f(r_i).\)
构造
令 $f(x) = x^{n-2}(x^2+3) + 4(x^{n-1} + x^{n-2} + \cdots + x + 1) + 2,$ 则对每个整数 $m$ 以及任意 $k \geq 2$ 个整数 $r_i, \ f(m) \equiv 2 \pmod 4, \ \prod^k_{i=1} f(r_i) \equiv 0 \pmod 4,$ 所以 $f(m) \neq \prod^k_{i=1} f(r_i).$官方构造
令 $f(x) = x(x+1)\cdots(x+n-1)+2$, 其余同理\(5.\) (高联 2011 T4) 在一个 \(3 \times 9\) 的方格中填上一些正整数. 如果有某个矩形中的所有正整数之和为 \(10\) 的倍数, 那么称这个矩形为“好矩形”;如果有一个格子不在任何一个“好矩形”中, 则称为“坏格”.求在这个 \(3 \times 9\) 的方格中的一种填法, 使得“坏格”最多, 最多为多少?
证明
令 $a_{ij}$ 表示第 $i$ 行第 $j$ 格填上的正整数, $A_{ij} = \sum^j_{k=1} a_{ik}, \ A_i = \sum^{9}_{j=1} A_{ij}.$对 $27$ 个坏格不存在的证明
若 $A_{ij} \equiv A_{ik} \pmod {10}(9\geq k>j > 0)$, 则 $A_{ik} - A_{ij} \equiv \sum^k_{h=j+1} a_{ih} \equiv 0 \pmod {10}$, 矛盾.故 $\forall i \in [1,3], \ A_{ij} \bmod 10$ 互不相同且不为 $0$, 即 $A_i \equiv \sum^9_{i=1} i \equiv 5 \pmod {10}.$ 故 $A_1 + A_2 \equiv 0 \pmod {10}.$ 又 $A_{1j} + A_{2j}$ 表示矩形 $(1,1)$ 到 $(2,j)$ 的和, 同理易得 $A_1 + A_2 \equiv \sum^9_{i=1} i \equiv 5 \pmod {10}$, 矛盾.对 $26$ 个坏格不存在的证明
若 $1 \times 1$ 的好矩形在第一行或第三行, 由上易得矛盾.若在第二行, 同理得 $A_1 + A_2 + A_3 \equiv A_2 + A_3 \equiv \sum^9_{i=1} i \equiv 5 \pmod {10}$, 由此得 $A_1 \equiv 0 \pmod {10}$, 矛盾.$25$ 个坏格的一个解
| 3 | 3 | 3 | 3 | 10 | 3 | 3 | 3 | 3 |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 7 | 7 | 7 | 7 | 10 | 7 | 7 | 7 | 7 |
\(6.\) (高联 2013 T2) 给定正整数 \(u, v\), 数列 \(\left\{a_n\right\}\) 定义如下: \(a_1 = u + v\), 对整数 \(m \geq 1\), \(a_{2m} = a_m + u, \ a_{2m+1} = a_m + v.\) 记 \(S_m = \sum^m_{i=1} a_i, \ m = 1,2,\cdots.\) 证明数列 \(\left\{S_n\right\}\) 中存在无穷多项是完全平方数.
证明
由 $S_{2m+1} = a_1 + \sum^m_{i=1} (a_{2i} + a_{2i+1}) = 2S_m + (m + 1)(u + v)$, 有 $S_{2^n-1} = 2S_{2^{n-1}-1} + 2^{n - 1}(u + v) = n2^{n - 1}(u + v).$ 当 $n = 2a^2(u + v), \ a \in \mathbb{N_+}$ 时, $S_{2^n-1} = [a(u+v)2^{a^2(u+v)}]^2$.\(7.\) (高联 2013 T4) 设 \(n, k\) 为大于 \(1\) 的整数, \(n < 2^k\). 证明: 存在 \(2k\) 个不被 \(n\) 整除的整数, 若将它们任意分成两组, 则总有一组有若干个数的和被 \(n\) 整除.
证明
令这 $2k$ 个整数为 $\pm 1, \ \pm 2, \ \cdots, \ \pm 2^{k-1}$. 若划分的其中一组含有 $\pm 2^i$, 则 $2^i+(-2^i) \mid n$, 若没有一组含有 $\pm 2^i$, 则其中必有一组为 $\left\{1,\ 2, \ \cdots,\ 2^k\right\}$. 由 $n < 2^k$, 则 $n = \sum^{k-1}_{i=0} a_i2^i, \ a_i \in \left\{0, 1\right\}.$ 故 $(\sum^{k-1}_{i=0} a_i2^i) \mid n$.\(8.\) (高联 2014 T4 推广) 设 \(m\) 为正整数, 整数 \(x_1,x_2,\cdots,x_m\) 模 \(m\) 互不同余, 整数 \(y_1,y_2,\cdots,y_m\) 模 \(m\) 互不同余. 证明: 一定存在一个 \(y_i\) 的排列 \(z_i\) 使得 \(x_i + z_i\) 模 \(2m\) 互不同余.
$m$ 为奇数
令 $z_i \equiv x_i \pmod m$ 即可.$m = 2q,\ q$ 为奇数
先设 $z_i \equiv x_i \pmod {m}$, 若 $z_i + x_i \equiv z_{i+q} + x_{i+q} \pmod {2m}$, 则交换 $z_i$ 与 $z_{i+q}$ 即可.不会证的
试证 $m = 2q, \ q$ 为偶数.\(9.\) (高联 2015 T4 推广) 设 \(p\) 为素数, 求所有正整数 \(k\) 使得 \(\forall n \in \mathbb{N_+},\ p^{(k-1)n+p-1} \nmid (\frac{kn!}{n!})^{p-1}.\)
提示
本题关键在于 $p$ 进制分解, $n$ 在 $p$ 进制下的最低次记为 $\nu_p(n)$, 系数和记为 $s_p(n)$. 命题等价于求所有正整数 $k$ 使得 $(k-1)n+p-2 \geq \nu_p(\frac{kn!}{n!})(p-1) = (kn-s_p(kn))-(n-s_p(n))$ 即 $s_p(kn) \geq s_p(n) - p + 2.$$k$ 是 $p$ 的幂
有 $s_p(kn) = s_p(n) \geq s_p(n)-p+2$.$k$ 不是 $p$ 的幂
令 $k = p^{\nu_p(k)}q$, 则$s_p(kn) = s_p(qn).$ 由欧拉定理 $q \mid p^{\varphi(q)t}-1,\ t \in \mathbb{N_+}$, 令 $n = \frac{p^{\varphi(q)t}-1}{q}+1,\ qn = p^{\varphi(q)t}+q-1$, 当 $t$ 足够大时, $s_p(qn) = s_p(q-1) + 1 \leq q.$ 而 $n = \frac{p^{\varphi(q)}-1}{q}\sum^t_{i=1}p^{\varphi(q)(i-1)}+1$, 有 $s_p(n) \geq 1+t > q+p-2 \geq s_p(kn)+p-2.$\(10.\) (高联 2016B T2) 设 \(n, k\) 为正整数, 且 \(n\) 为奇数. 已知 \(2n\) 的不超过 \(k\) 的正约数的个数为奇数, 证明 \(2n\) 存在约数 \(d\) 属于 \((k,2k]\).
证明
令 $s$ 表示 $2n$ 的不超过 $2k$ 的奇因子个数, $t$ 表示偶因子个数, 则 $s \neq t.$假设不存在 \(d\) 满足条件.
由若 \(2\mid d,\ d \mid 2n\), 则 \(\frac{d}{2} \mid 2n\), 可知 \(t \leq s.\)
由若 \(2 \nmid d,\ d \mid 2n\), 则 \(2d \mid 2n\), 可知 \(s \leq t\), 矛盾.
\(11.\) (高联 2016A T4) 设 \(p\) 与 \(p+2\) 均是素数, \(p>3.\) 数列 \(\left\{a_n\right\}\) 定义为 \(a_1 = 2, a_n = a_{n-1} + \lceil \frac{pa_{n-1}}{n} \rceil.\) 证明: \(\forall n \in [3,p-1] \cap \mathbb{N},\ n \mid pa_{n-1}+1\) 成立.
证明
因为 $p,\ p+2$ 均为素数且大于 $3$, 所以 $p \bmod 3 = 2$. 又 $a_2 = p + 2$, 所以 $pa_2+1 = p(p+2)+1 \equiv 0\pmod3$.若当 \(k \leq n < p-1\) 时, \(k \mid pa_{k-1} + 1\) 均成立, \(a_n = a_{n-1} + \frac{pa_{n-1}+1}{n}\), 那么 \(pa_n + 1 = \frac{n+p}{n}(pa_{n-1} + 1) = \frac{2(p+n)!}{n!(p+2)!}(p+1)^2\) .
将等式变形, 有 \(n!p(p+2)(pa_n+1) = \frac{(p+n)!}{(p-1)!}2(p+1).\) 因为 \(\binom{p+n}{n+1} = \frac{(p+n)!}{(n+1)!(p-1)!}\), 所以 \((n+1)! \mid \frac{(p+n)!}{(p-1)!}\), 从而 \(n+1 \mid p(p+2)(pa_n+1).\) 因为 \(n+1 < p\), 所以 \((n+1,p(p+2))=1\), 从而 \(n+1 \mid pa_n+1.\)
\(12.\) (高联 2017 T4) 设 \(m,n\) 均是大于 \(1\) 的整数. \(a_1,a_2,\cdots,a_n\) 为不超过 \(m\) 的互不相同的正整数, 且 \(a_1,a_2,\cdots,a_n\) 互素. 证明: 对于任意实数 \(x\), 均存在 \(i\) 使得 \(\lvert\lvert a_ix \rvert\rvert \geq \frac{2}{m(m+1)}\lvert\lvert x \rvert\rvert\), 这里 \(\lvert\lvert y \rvert\rvert\) 表示实数 \(y\) 到与它最近的整数的距离.
证明
由裴蜀定理, 存在整数 $x_1,x_2,\cdots,x_n$ 使得 $\sum^n_{i=1} x_ia_i = (a_1,a_2,\cdots,a_n) = 1$, 且 $\sum^n_{i=1}\lvert x_i\rvert < \sum^n_{i=1} a_i.$对后者的证明
不妨设 $a_i$ 递增. 设 $x_1 = q_2a_2 + r_1(\lvert r_1 \rvert \leq \frac{a_2}{2}),$ $x_i + q_ix_{i-1} = q_{i+1}a_{i+1}+r_i(\lvert r_i \rvert \leq \frac{a_{i+1}}{2}, 2 \leq i \leq n-1).$ 则 $\sum^{n-1}_{i=1} r_ia_i + (x_n+q_nx_{n-1})a_n = 1.$ 因为 $x_n+q_nx_{n-1} = \frac{1-\sum^{n-1}_{i=1}r_ia_i}{a_n} \leq \sum^{n-1}_{i=1} \lvert r_i \rvert$, 所以 $\sum^{n-1}_{i=1} r_i +(x_n+q_nx_{n-1}) \leq \sum^n_{i=2} a_i < \sum^n_{i=1} a_i.$假设存在 \(x_0\) 使得对任意 \(i\) 都有 \(\lvert\lvert a_ix_0 \rvert\rvert < \frac{2}{m(m+1)}\lvert\lvert x_0 \rvert\rvert.\) 易得 \(x_0\) 不是整数.
那么 \(\lvert\lvert x_0 \rvert\rvert \leq \sum^n_{i=1} \lvert\lvert x_i a_ix_0 \rvert\rvert \leq \sum^n_{i=1} x_i\lvert\lvert a_ix_0 \rvert\rvert < \sum^n_{i=1}a_i\frac{2}{m(m+1)}\lvert\lvert x_0 \rvert\rvert\), 从而 \(\sum^n_{i=1} a_i > \frac{m(m+1)}{2} = \sum^m_{i=1}i\), 显然矛盾.
组合数学
\(1.\) (高联 2015 T2) 设 \(S = \left\{A_1,A_2,\cdots,A_n\right\}\), 其中 \(A_1,A_2,\cdots,A_n\) 是 \(n\) 个互不相同的有限集合 \((n \geq 2)\), 满足对任意的 \(A_i,A_j \in S\), 均有 \(A_i \cup A_j \in S\), 若 \(k = \min^n_{i=1} \lvert A_i \rvert\), 证明: 存在 \(x \in \bigcup^n_{i=1} A_i\), 使得 \(x\) 属于 \(A_1,A_2,\cdots,A_n\) 中的至少 \(\frac{n}{k}\) 个集合.
不妨设 \(\lvert A_1 \rvert = k, \ A_1 = \left\{x_1,x_2,\cdots,x_k\right\}\), 可将 \(A_2,\cdots,A_n\) 分为三类.
第一类: \(A_j \cap A_i = \varnothing\), 共有 \(s\) 个;
第二类: \(\varnothing \not= A_j \cap A_i \not= A_i\), 共有 \(n-s-t-1\) 个;
第三类: \(A_j \supseteq A_i\), 共有 \(t\) 个.
由第一类 \(A_j \cup A_i \in S\) 必属于第三类, \(s \leq t\).
令 \(a_i\) 表示 \(x_i\) 属于 \(S\) 中的集合个数, 则 \(\sum^k_{i=1} x_i \geq k(1+t) + (n-s-t-1) \geq 2(1+t)+(n-2t-1) = n+1.\) 故存在 \(x \in A_1, \ x\) 属于至少 \(S\) 中至少 \(\frac{n}{k}\) 个集合.
\(2.\) (\(\rm Sperner\) 定理) 设 \(I\) 为 \(n\) 元集, \(A_1,A_2,\cdots,A_m\) 为 \(I\) 的子集, 且互不包含, 则 \(m\) 最大值为 \(\binom{n}{[\frac{n}{2}]}.\)
对于每个 \(i \in [1,n]\), 生成关于 \(A_i\) 的 \(1 \sim n\) 的排列, 满足前 \(\lvert A_i \rvert\) 个数属于 \(A_i\).
易得生成的所有排列个数为 \(\sum^m_{i=1} \lvert A_i \rvert!(n - \lvert A_i \rvert)! \leq n!\), 变形得 \(1 \geq\sum^m_{i=1} \frac{\lvert A_i \rvert!(n - \lvert A_i \rvert)!}{n!} = \sum^m_{i=1} \frac{1}{\binom{n}{\lvert A_i \rvert}} \geq \frac{m}{\binom{n}{[\frac{n}{2}]}}\)
故 \(m \leq \binom{n}{[\frac{n}{2}]}\), 当 \(A_i\) 均为 \([\frac{n}{2}]\) 元子集时取等.
应用: \(11\) 个歌唱演员参加联欢节, 每天有一些演员演出, 其余的演员在台下观看, 联欢节结束时, 每个演员都至少以观众身份看过其他演员的一次演出.问此联欢节至少持续了多少天?
用 \(A_i\) 表示第 \(i\) 个演员在台下观看天数的集合, 因为每个演员都看过对方的演出, 所以 \(A_i\) 互不包含. 设联欢节持续了 \(n\) 天, 由 \(\rm Sperner\) 定理, \(\binom{n}{[\frac{n}{2}]} \geq 11\), 即 \(n \geq 6\).
\(3.\) (\(\rm Erdos-Szekeres\) 定理) 任意一个 \(mn+1\) 项的实数数列, 可以从中选出 \(m+1\) 项非严格单调递增或者选出 \(n+1\) 项非严格单调递减.
若最多能选出 \(m\) 项非严格单调递增和 \(n\) 项非严格单调递减, 用 \(a_i\) 表示以第 \(i\) 项结尾的最长上升子序列的长度, 用 \(b_i\) 表示最长下降子序列的长度. 则 \((a_i,b_i)\) 互不相同, 且 \(a_i \leq m,b_i \leq n.\) 则最多有 \(mn\) 项.
\(4.\) 在一次演讲中, 有 \(5\) 位数学家每人均打两次盹,并且每两人均有同时在打盹的时刻. 证明: 一定有三个人, 他们有同时打盹的时刻.
设每一个盹为一个顶点, 两个顶点有连边当且仅当时间有交, 题目等价于证明 \(\lvert V \rvert = 10, |E| = \binom{5}{2} = 10\) 的图 \(G\) 存在环, 而这是显然的.
不等式
\(1.\) (\(\rm Cauchy-Schwarz\) 不等式) \((\sum a_ib_i)^2 \leq (\sum a_i^2)(\sum b_i^2).\) 取等当且仅当 \(a_i,\ b_i\) 对应成比例.
\((\rm i)\) (\(\rm Lagrange\) 恒等式) \((\sum a_i^2)(\sum b_i^2) = (\sum a_ib_i)^2 + \sum^n_{i=1}\sum^n_{j=i+1} (a_ib_j - a_jb_i)^2.\)
将左右展开, \(\sum^n_{i=1}\sum^n_{j=1} a_i^2b_j^2 = \sum a_i^2b_i^2 + 2\sum^n_{i=1}\sum^n_{j=i+1} a_ia_jb_ib_j + 2\sum^n_{i=1}\sum^n_{j=i+1} a_i^2b_j^2 - 2\sum^n_{i=1}\sum^n_{j=i+1} a_ia_jb_ib_j\), 显然等价.
考虑 \(n\) 维向量 \(\boldsymbol a = (a_1,a_2,\cdots,a_n), \boldsymbol b =(b_1,b_2,\cdots,b_n)\), 则 \((\lvert \boldsymbol a \rvert\lvert \boldsymbol b \rvert)^2 = (\lvert \boldsymbol a \rvert\lvert \boldsymbol b \rvert \cos \theta)^2 + (\lvert \boldsymbol a \rvert\lvert \boldsymbol b \rvert \sin \theta)^2 = (\boldsymbol a \cdot \boldsymbol b)^2+(\boldsymbol a \times \boldsymbol b)^2\), 当 \(n = 3,\ 7\) 时即原恒等式.
\((\rm ii)\) 由 \(\boldsymbol a \cdot \boldsymbol b = \sum a_ib_i\), 有 \(\forall k \in \mathbb{R}, (k\boldsymbol a + \boldsymbol b)^2 = \boldsymbol a^2k^2 + 2(\boldsymbol a \cdot \boldsymbol b)k + \boldsymbol b^2 \geq 0.\) 则 \(\Delta = 4(\boldsymbol a \cdot \boldsymbol b)^2 - 4\boldsymbol a^2 \boldsymbol b^2 \leq 0,\) 当且仅当 \(\boldsymbol a = k\boldsymbol b\) 或 \(\boldsymbol b = \boldsymbol 0\) 时取等.
\((\rm iii)\) 几个变形: 对 \(b_i > 0\), 有 \(\sum b_i \sum \frac{a_i^2}{b_i} \geq (\sum a_i)^2\), 将 \(\sum b_i\) 移到右边有 \(\sum \frac{a_i^2}{b_i} \geq \frac{(\sum a_i)^2}{\sum b_i}.\) 可将平方中的数相加.
几何
\(1.\) (彭赛列小定理) \(F_1,F_2\) 分别为椭圆左右焦点, 过椭圆外一点 \(P\) 作椭圆切线 \(PA,PB.\) 证: \(\ang APF_1 = \ang BPF_2.\)
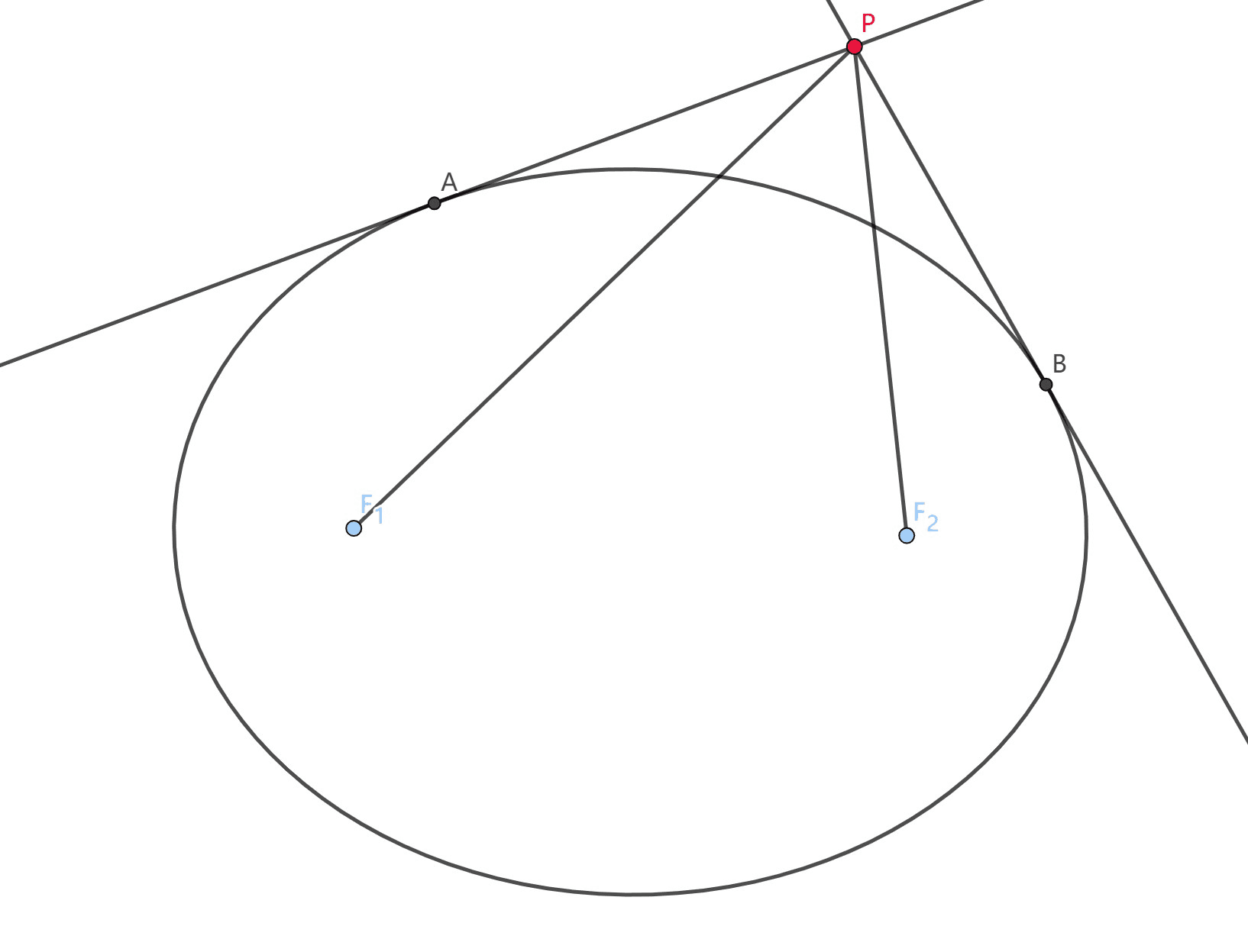
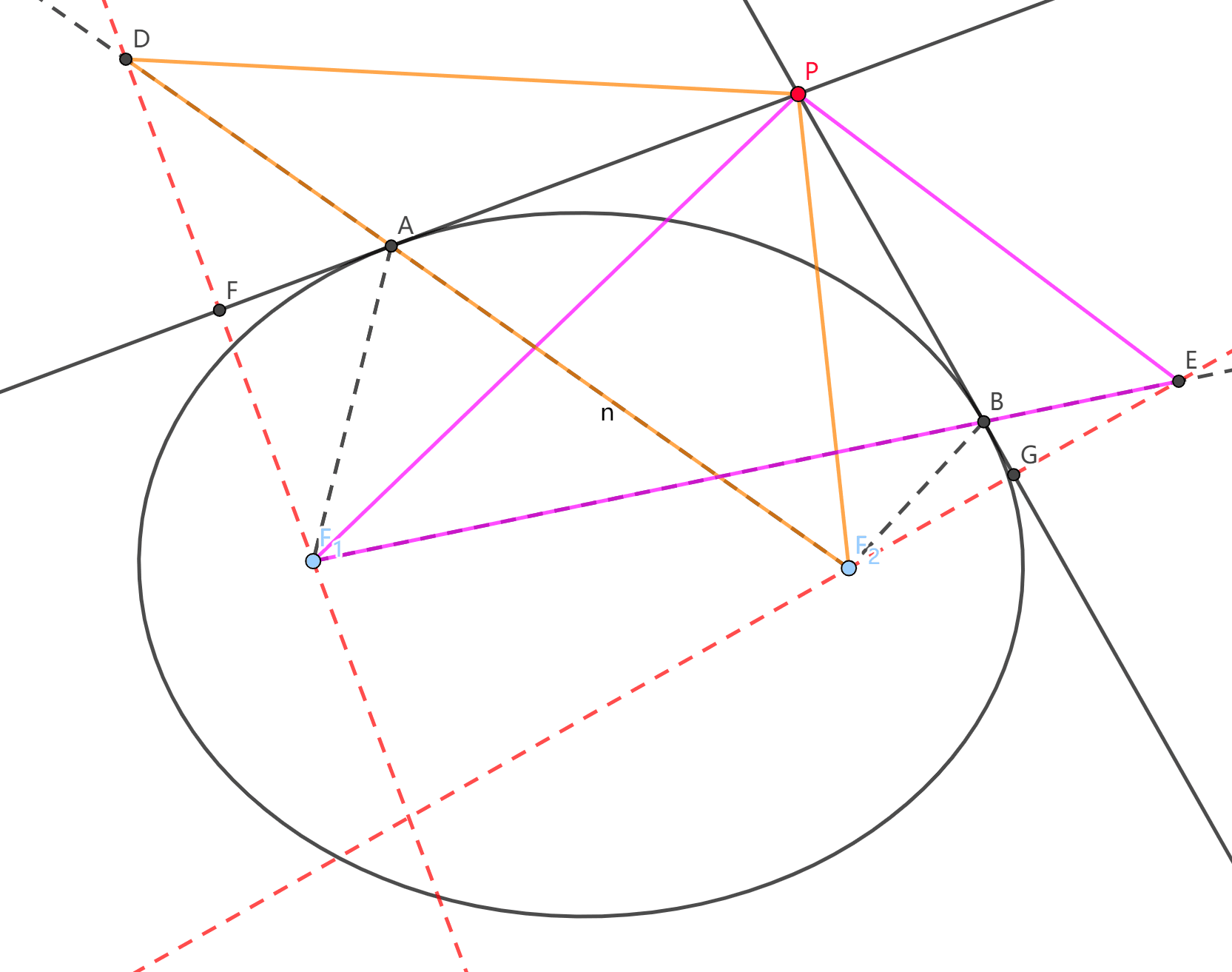
红虚线是垂线, 由椭圆的光学性质, \(\ang F_1AF = \ang F_2AP = \ang FAD\), 然后橙三角就和紫三角全等楽! 证完了睡觉去了.
例题的推广
\(1.\) 令 \(N \in \mathbb{N^+}, S = [1,N]\cap \mathbb{N^+}, \forall n \in S, S_n = \sum_{sym}^n a_i > 0\), 证明 \(\forall i\in S, a_i > 0.\)
由 \(f(x) = \prod^N_{i=1} (x-a_i) = \sum_{s \subseteq S}(-1)^{|s|} x^{N-|s|}\prod_{i\in s} a_i = \sum^N_{n=1} S_n(-1)^nx^{N-n}, \ f(a_i) = 0\), 得 \(a_i > 0.\)


