第04次作业-树

第04次作业-树

1.学习总结

1.1树结构思维导图

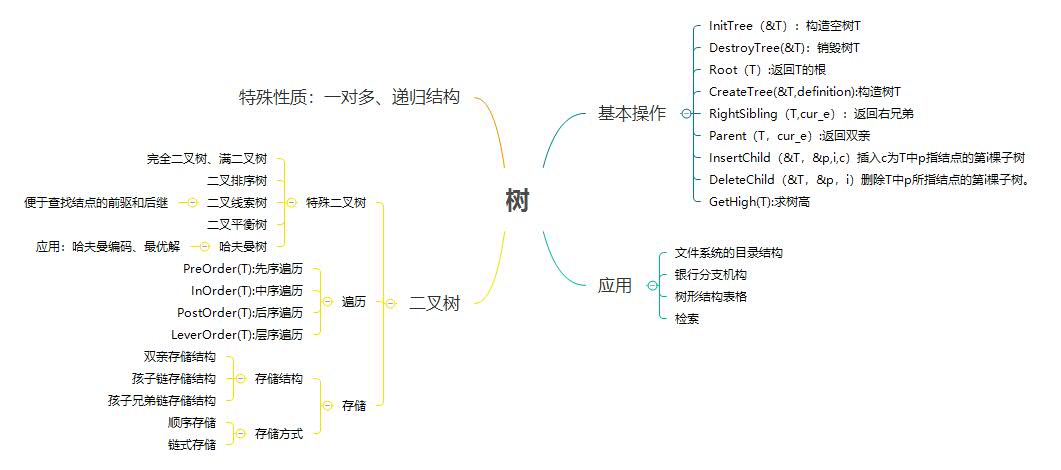
1.2 树结构学习体会

• 对树的认识
  树是一个一对多的递归结构，包含有序树和无序树。无序树中的二叉树为重要学习部分。
  二叉树的度最大为2，可用链式和顺序存储方式存储。包含二叉排序树、线索二叉树、哈夫曼树、平衡二叉树等特殊二叉树。
  二叉树的遍历包含先序遍历、中序遍历、后序遍历和层次遍历。
• 学习过程中遇到的困难
  对树的性质和术语理解不清
  对平衡二叉树的LR LL RL RR 等具体操作不理解
  在哈夫曼树计算 WPL 时曾忘记他是二叉树
  不能很好的利用树的递归思想
  代码不会写是一个很大的困难了
• 树结构可以解决的问题
  文件系统的目录结构
  相比数组和链表查找速度更快，为O(logn)

2.PTA实验作业

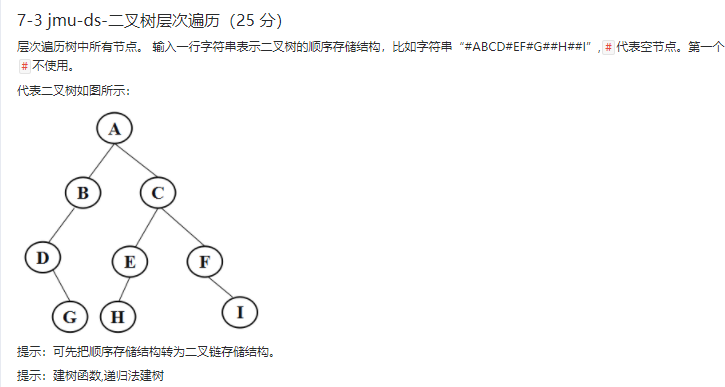
2.1 题目1：7-3 jmu-ds-二叉树层次遍历

2.2 设计思路

void LeverOrder( BTNode *b)
/* 层序遍历 */
定义树的指针型变量 p
定义队列 qu 用于存储树的指针变量

将树的根节点入队

if b 不为空
    then while 队不为空
                队首元素 ← p
                DeQueue ( qu )
                输出 p->data
                if p->lchild 不为空
                    then Enqueue( p->lchild )
                if p->lchild 不为空
                    then Enqueue( p->lchild )
                 end

BTree trans(string str,int i)
/*递归建立二叉树 */
定义树的指针型变量 b 
if i > str.size()
    then 返回空
if str[i] = '#'
    then 返回空
b->data ← str[i]
递归建立左子树
递归建立右子树

2.3 代码截图

• 结构体定义及函数声明
  
• 主函数
  
• 二叉树层序遍历
  
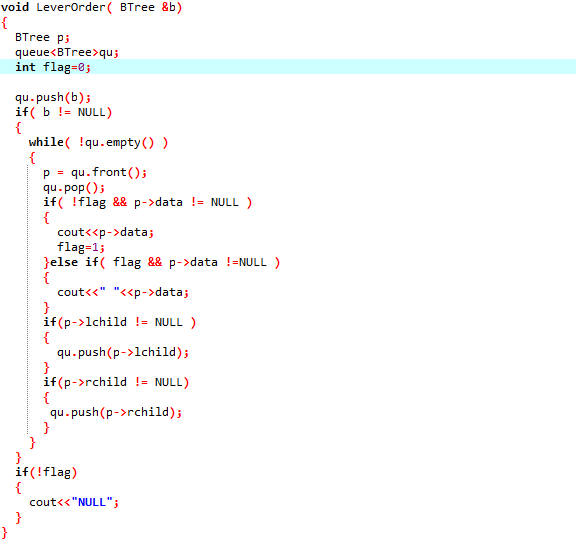
• **递归建立二叉树 **
  

2.4 PTA提交列表说明

• 段错误：没有考虑到 str[i] 为空的情况
  解决方法：添加代码if(i>str.size()) { return NULL; }
• 答案错误：队列不为空没有包含在 b 不为空的条件下
  解决方法：询问同学后解决

2.1 题目2：7-2 根据后序和中序遍历输出先序遍历

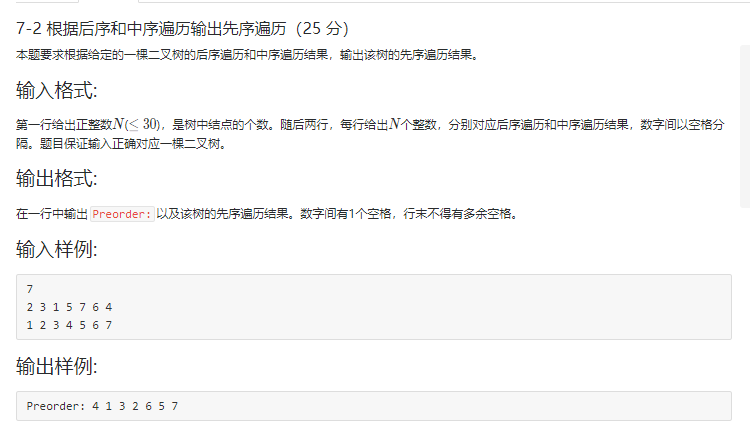
2.2 设计思路

BTNode *CreateBTree( int n,int *in,int *post)
/*利用后序和中序递归建树 */
定义树的指针变量  BT
定义 int 型变量 i
if n < 0 
    then 返回 空
BT->data ← post[n-1]
将 BT 的左右子树置为空
for i=0 to n
    if in[i] = BT->data
        then break
end
递归创建左子树
递归创建右子树

2.3 代码截图

• 结构体定义及函数声明
  
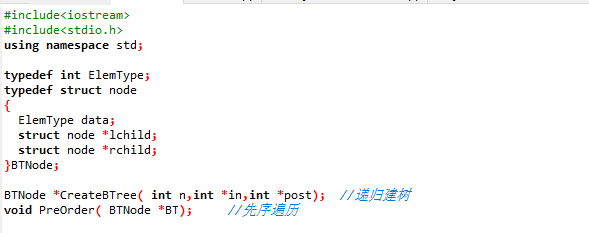
• 主函数
  
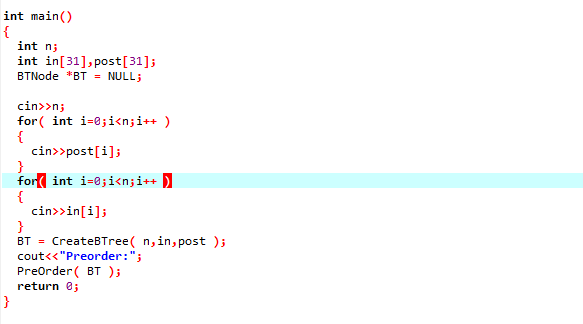
• 利用后序和中序递归建树
  

2.4 PTA提交列表说明

• 答案错误：忘记了数组只存储到 n-1 个位置的性质，在调用函数创建右子树时传入的 n 写成了 n-i
  解决方法：修改代码 CreateBTree( n-i-1,in+i+1,post+i)
• 段错误：没有将 BT 的左右子树置为空
  解决方法：添加代码BT->lchild = BT->rchild = NULL;

2.1 题目3：6-4 jmu-ds-表达式树

2.2 设计思路

/*建表达式的二叉树*/
定义 int 型变量 i 记录字符串位置
定义树的指针型变量 rtemp ltemp
定义树指针型变量的栈 digit optr 分别用于存储运算数和运算符

将 '#' 进栈    /*作为标记*/

while str[i] 不为空
    if str[i] 为操作符
        then 创建结点并入栈
        else        /*判断当前运算符和栈顶运算符的优先级*/
            then if optr栈 栈顶运算符优先级高
                        then 出 optr栈 元素并创建结点 T
                                T->rchild ←出 digit栈 元素,  T->lchild ←出 digit栈 元素
                        elseif optr栈 栈顶元素优先级低
                            then 入栈当前运算符
                        else
                            出 optr 栈运算符
    end

while optr栈顶元素 ≠ ‘#’
    出 optr栈 元素并创建结点 T
    T->rchild ←出 digit栈 元素,  T->lchild ←出 digit栈 元素
    end
T ← digit栈 栈顶元素

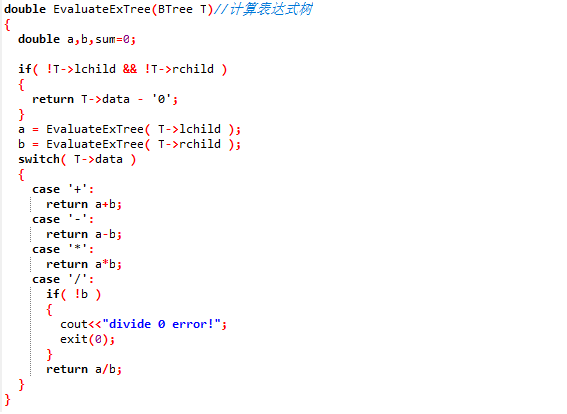
double EvaluateExTree(BTree T)
/* 计算表达式树 */
定义 int 型变量 a b
if T 为叶子结点
    then 返回 T 所指的数值
    else
        a ← EvaluateExTree( T->lchild )
        b ← EvaluateExTree( T->rchild )
        用 T 的运算符来处理 a b

2.3 代码截图

• 建表达式的二叉树
  
  
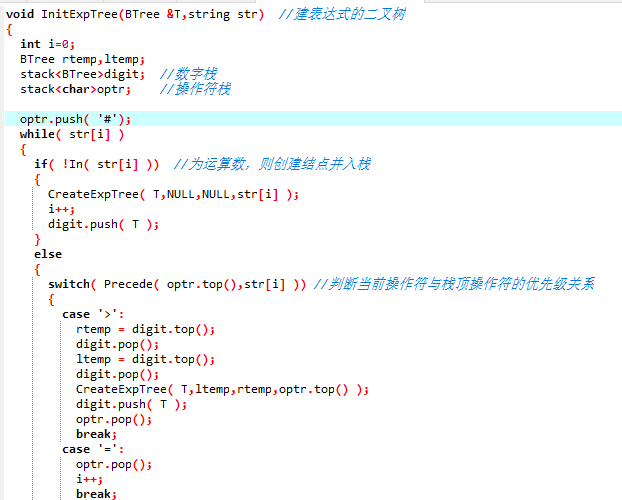
• 计算表达式树
  

2.4 PTA提交列表说明

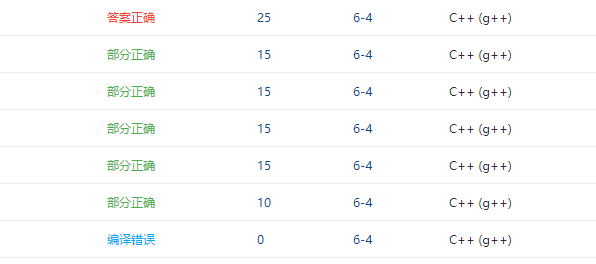
• 段错误：在调用优先级判断函数时写成Precede( str[i],optr.top() )
  解决方法：注意到题目中的判断优先级函数中没有 t1 为 ‘）’ 的情况，修改代码为Precede( optr.top(),str[i] )
• 答案错误：没有在一开始让 ‘#’ 入栈
  解决方法：后面询问同学知道，需要做这样一个标记

3.1 PTA排名截图

3.2 我的总分：2分

4.阅读代码

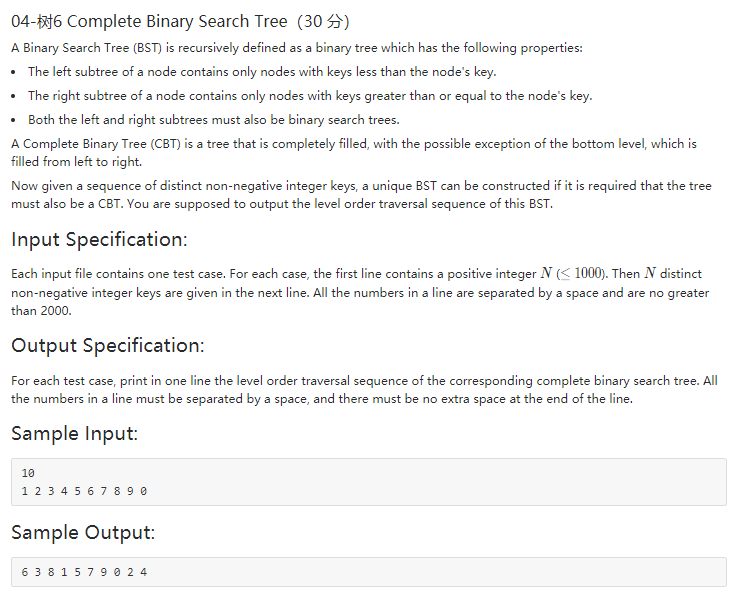
题意：要求构造完全二叉排序树，并层序遍历输出
数组实现：利用完全二叉树的性质，用数组存储的话，父节点下标为i,左孩子为2i，右孩子为2i+1。而一个完全二叉搜索树的最小节点肯定在最左边。

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;

int N;
int pos=0;
int *tree;
vector<int> vec;

void build(int n)
{
    if (n>N) return;
    else
    {
        build(n*2);
        tree[n] = vec[pos++];
        build(n*2+1);
    }
}

int main()
{
    int element;
    cin >> N;
    tree = new int [N+1];
    //输入元素并排序
    for (int i=0;i<N;i++)
    {
        cin >> element;
        vec.push_back(element);
    }
    sort(vec.begin(),vec.end());
    
    build(1);
    cout << tree[1];
    for (int i=2;i<=N;i++)
        cout << ' ' << tree[i];
    return 0;
}

链式结构实现：先把输入数据放在一个vector里面，然后排序，从小到大排。然后找出整个树的根节点的下标（找的方法是先计算左子树有几个节点），再递归，在左子树再建树。

#include<iostream>
#include<vector>
#include<cmath>
#include<queue>
#include<algorithm>
using namespace std;

typedef struct node* tree;
struct node
{
    int data;
    tree left;
    tree right;
};

tree BuildTree (tree,int,unsigned,unsigned);
int FindRoot(int,int);
void LevelOrderTraversal(tree T);
vector<int> vec;

int main()
{
    int N,element;
    cin >> N;
        
    //输入元素并排序
    for (int i=0;i<N;i++)
    {
        cin >> element;
        vec.push_back(element);
    }
    sort(vec.begin(),vec.end());
    
    unsigned b=0,e=vec.size()-1;

    int root=FindRoot(N,0);
    tree T = nullptr;    
    T=BuildTree(T,root,b,e);

    LevelOrderTraversal(T);

    return 0;
}

int FindRoot(int N,int base)
{
    int level=int(log(double(N))/log(2.0))+1; //共有这么多层
    int root=1;
    if (N == 1)
        root = 0;
    else if (N == 2)
        root = 1;
    else if (N==3)
        root = 1;
    else
        if (N-(pow(double(2),double(level-1))-1) > pow(double(2),double(level-2)) )//左子树满了
            root = pow(double(2),double(level-1))-1;
        else
            root = pow(double(2),double(level-2))-1+N-(pow(double(2),double(level-1))-1);
    return root+base;
}

tree BuildTree(tree T,int root,unsigned b,unsigned e)
{
    //cout << b << e << endl;
    if (e==b)
    {
        T=new node;
        T->data = vec[b];
        T->left = nullptr;
        T->right = nullptr;
    }
    else
    {
        T = new node;
        T->data = vec[root];
        T->left = BuildTree(T,FindRoot(root-b,b),b,root-1);
        if (e!=root)
            T->right= BuildTree(T,FindRoot(e-root,root+1),root+1,e);
        else
            T->right = nullptr;
    }
    return T;
}

void LevelOrderTraversal(tree T)
{
    bool flag=true;
    queue<tree> Q;
    if (!T) return;
    Q.push(T);
    while (!Q.empty())
    {
        if (flag)
        {
            cout << Q.front()->data;
            flag = false;
        }
        else
            cout << ' ' << Q.front()->data;
        if (Q.front()->left)
            Q.push(Q.front()->left);
        if (Q.front()->right)
            Q.push(Q.front()->right);
        Q.pop();
    }
}

• 二叉搜索树的中序遍历的结果就是递增排列的，那么我们采用中序遍历的方法去建树(即遍历的时候，遍历操作是给节点赋值，即采用中序遍历的方法，利用完全二叉树的父子节点关系去建树，最后把数组按序输出即可)。通过这次阅读代码学习到了逆向思维的方式，以后在做题的时候也会考虑到。
  代码来源：(https://www.cnblogs.com/xian-ye/p/5204096.html)

5. 代码Git提交记录截图