EM算法

1.什么是极大似然函数，用来解决什么实际问题？

似然函数是一种关于统计模型中的参数的函数，表示模型参数中的似然性。“似然性”与“或然性”或“概率”意思相近，都是指某种事件发生的可能性。而极大似然就相当于最大可能的意思。

比如你一位同学和一位猎人一起外出打猎，一只野兔从前方窜过。只听一声枪响，野兔应声到下，如果要你推测，这一发命中的子弹是谁打的？你就会想，只发一枪便打中，由于猎人命中的概率一般大于你那位同学命中的概率，从而推断出这一枪应该是猎人射中的。

最大似然估计是知道结果，然后寻求使该结果出现可能性最大的条件，以此作为估计值

概率是根据条件推测结果，而似然则是根据结果反推条件。在这种意义上，似然函数可以理解为条件概率的逆反。

求极大似然函数估计值的一般步骤：

1.写出似然函数；

2.对似然函数取对数，并整理；

3.求导数，令导数为0，得到似然方程；

4.解似然方程，得到的参数即为所求；   

2.EM算法是什么，用来解决什么问题？

最大期望算法（Expectation-maximization algorithm，又译为期望最大化算法），是在概率模型中寻找参数最大似然估计或者最大后验估计的算法，其中概率模型依赖于无法观测的隐性变量。

最大期望算法经过两个步骤交替进行计算：

第一步是计算期望（E），利用对隐藏变量的现有估计值，计算其最大似然估计值；

第二步是最大化（M），最大化在E步上求得的最大似然值来计算参数的值。M步上找到的参数估计值被用于下一个E步计算中，这个过程不断交替进行。

例子

抛硬币，有两个硬币，但是两个硬币的材质不同导致其出现正反面的概率不一样，目前我们只有一组观测数据，要求出每一种硬币投掷时正面向上的概率。总共投了五轮，每轮投掷五次，现在先考虑一种简单的情况，假设我们知道这每一轮用的是哪一个硬币去投掷的：

 

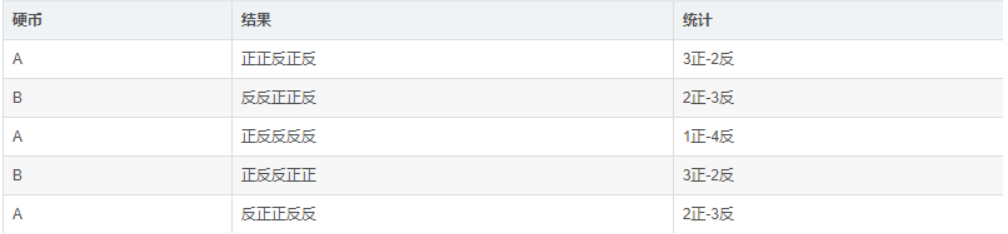
 那么我们拿着这样的一组数据，就可以很轻松的估计出A硬币和B硬币出现正面的概率，如下：

   PA = （3+1+2）/ 15 = 0.4

  PB= （2+3）/10 = 0.5

 现在把问题变得复杂一点，假设我们不知道每一次投掷用的是哪一种硬币，等于是现在的问题加上了一个隐变量，就是每一次选取的硬币的种类。

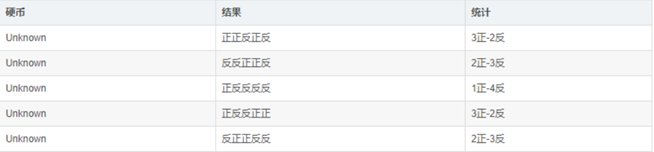
 假设我们把每一次硬币的种类设为z,则这五次实验生成了一个5维的向量(z1,z2,z3,z4,z5)，现在问题来了，如果我们要根据观测结果去求出PA,PB，那么首先需要知道z，但是如果用最大似然估计去估计z，又要先求出PA,PB。这就产生了一个循环。那么这个时候EM算法的作用就体现出来了，

EM算法的基本思想是：先初始化一个PA,PB，然后我们拿着这个初始化的PA,PB用最大似然概率估计出z，接下来有了z之后就用z去计算出在当前z的情况下的PA,PB是多少，然后不断地重复这两个步骤直到收敛。

假设初始状态下PA=0.2, PB=0.7，然后我们根据这个概率去估计出z：

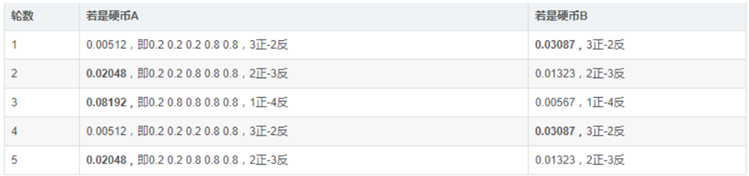
 按照最大似然估计，z=(B,A,A,B,A)，有了z之后我们反过来重新估计一下PA,PB：

         PA = （2+1+2）/15 = 0.33

         PB =（3+3）/10 = 0.6

        可以看到PA,PB的值已经更新了