量化交易中组合优化的那些事儿
简介
组合优化，本质上是LP和QP的凸优化问题，设定多个交易约束，最大化某一目标函数。/n
比如：非空约束下，求解资产占比，使得给定风险下，收益最大化或者 同收益情况下，风险最小化。
方法论
- 确定目标函数
- 确定约束
- 算法求解
拓展
不同的应用场景，不同的侧重点，我们可以建立不同的优化目标和约束。随着金融理论的发展，各种优化器也应运而生。
在这里，我简单举个例子，让大家理解下几种常用理论的混合使用。
以最经典的Markowitz理论为例：
简单来说，这个优化目标就是 最大化（组合收益-风险偏好*组合风险)
式子中的μ 表示资产的预期收益率，一般地，我们可以使用资产的历史收益率去估算这个收益率矩阵。显而易见，预期收益率的不同，一定会影响求解的结果，
所以也就衍生出一系列模型去优化 预期收益率 以及 协方差矩阵 的估计算法，比如：Black Litterman model, Risk Factor model。
当我们使用因子模型时，我们可以重新定义优化问题:
现在优化目标仍然是收益与风险之间的权衡。约束包括 权重总和为1、因子暴露约束、仓位暴露约束。
这里组合资产风险变成了 因子风险(组合的因子暴露矩阵×因子协方差矩阵×组合的因子暴露矩阵的转置)以及资产风险的总和。
自然而然，我们就会思考，用哪些因子来搭建这个factor model，这时候 大名鼎鼎的barra因子就可以隆重登场了。
获取到barra因子数据，开始计算单资产的因子暴露F(这里是单资产的暴露 f才是组合的因子暴露)，因子协方差矩阵以及资产风险对角矩阵。
关于因子暴露度 可以参考米框的做法
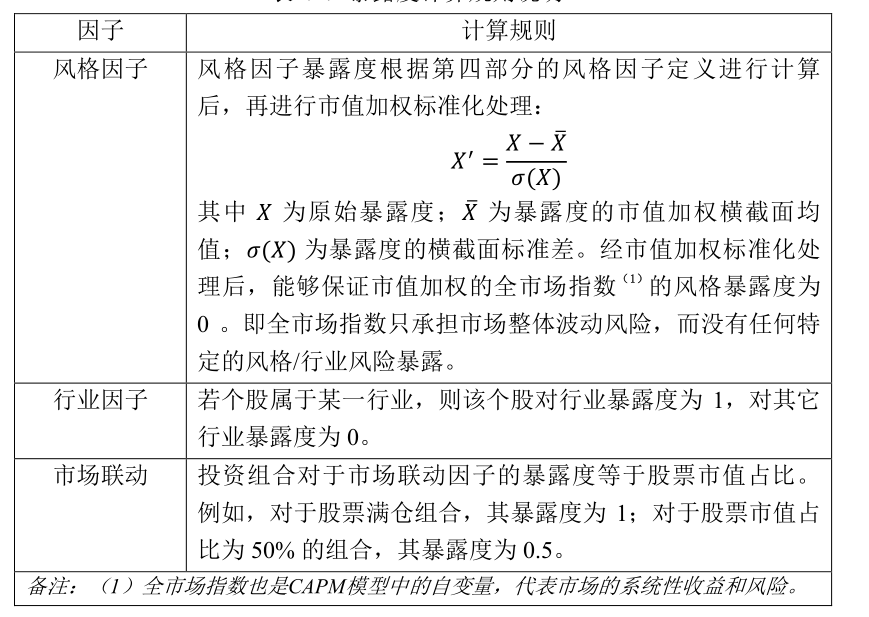
求解得因子暴露度矩阵F 可以获得每一期的因子收益率，获得因子收益率之后求解得到协方差矩阵。
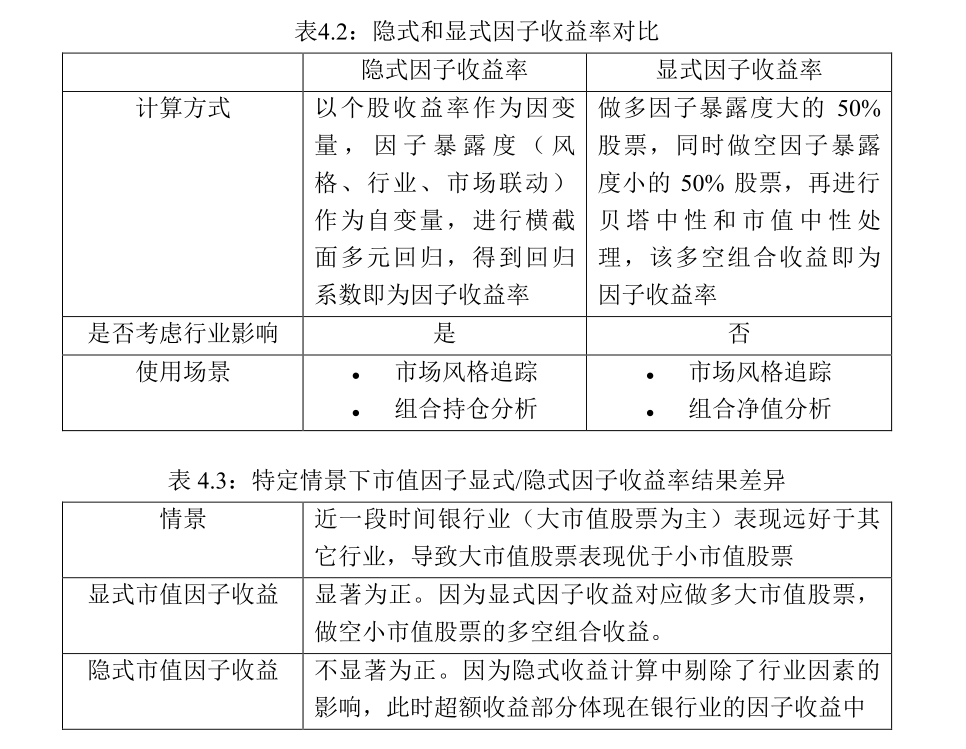
使用隐式计算法 线性回归拟合 asset returns=β0+β1×factor1_exposure+β2×factor2_exposure+…+βN×factor_exposureN+ϵ（系数β即收益率）
可以看出，不同的资产池， 会影响因子收益率的计算，最终导致组合放入实盘时的效果，所以针对不同的策略 选择不同的因子收益计算方法和样本也是需要考虑的一部分。
执行优化器，即可求得不同的γ系数下的解。
一些优化想法
- 对多因子策略进行因子系数优化
最大化IC 同时将IC的波动 以及换手作为惩罚项
max W*IC - λW∑W - (W-W1)
