基于RiceQuant的期货多因子策略实现(一)

前言

基于多因子模型理论，介绍其在国内期货的应用，并使用米宽（RiceQuant）的RQFactor进行实现。

理论基础

CAMP：资产的预期超额收益由市场组合的预期超额收益与资产对市场风险的暴露决定

=========================================》

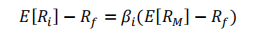
APT：在 CAPM 的基础上进行了延伸,将决定资产收益率的风险来源扩充至多个因子

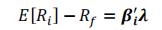
更加合理的表达式,考虑存在一个定价误差

=========================================》

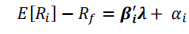
MFM:等价于APT，换个表现形式

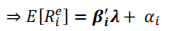
算子与因子

算子

定义：面向因子可复用的逻辑操作

进阶：根据算子的操作纬度可以将算子分为3大类

时序算子
每个标的的因子逻辑操作，只涉及该标的因子数据。
根据时序算子的复杂度，可以继续划分:

简单算子
一种算子计算的结果只与输入因子的当期值有关，这种算子输出的因子值长度与输入因子值相同
如:+,-,LOG
滑动窗口算子
根据输入因子的一个时间序列进行计算
如:MA,SUM，TS_RANK

特别的，如REF算子，可以看做是简单算子（因为python提供了便捷的shift操作，让用户不必调用滑动窗口就能获取到值），
也可以作为滑动窗口算子（REF涉及到了时间序列操作）

截面算子
每个标的的因子逻辑操作，涉及该标的因子数据以及标的池中其他标的的因子数据
如：RANK

因子

定义：描述 某个标的 在 某个周期的特征。

进阶：根据因子的依赖因子构成可以将算子分为2大类

基础因子
基础因子的生成，不依赖其他因子

open,high,low,close,volume等可直接获取的行情数据
仓单,基本面等需要进行数据处理但不依赖其他因子数据

复合因子
复合因子本质是算子应用于单个或多个因子(包含基础因子以及复合因子)所派生的因子
因此，基于他们所依赖的算子，根据算子的复杂度，可以进一步划分
- 简单复合因子
  =》因子 + 简单算子
  =》如： LOG（OPEN-CLOSE）-->依赖因子：OPEN，CLOSE 依赖算子: LOG,-
- 滑动窗口因子
  =》因子 + 滑动窗口算子 + （简单算子）
  =》如： TS_RANK(CLOSE- MA(CLOSE,20)) -->依赖因子：CLOSE 依赖算子: TS_RANK,MA,-
- 截面复合因子
  =》因子 + 截面算子 +（滑动窗口算子 + 简单算子）
  =》如： RANK（TS_RANK(CLOSE- MA(CLOSE,20))） -->依赖因子：CLOSE 依赖算子: RANK，MA, -

米框提供的基类

因子
- 自定义因子 ==》 UserDefinedLeafFactor (原型为 UserDefiendLeafFactor(name, func)， func返回一个序列作为因子返回值)
算子
- 简单算子 ==》CombinedFactor(func, factors): 定义在rqfactor.extension中；其接受的func原型为func(series);
- 滑动窗口算子 ==》RollingWindowFactor(func, window, factor): 定义在rqfactor.extension中；func函数原型为def func(series, window);
  ==》CombinedRollingWindowFactor(func, window, *factors): 定义在rqfactor.extension中，接受多个因子作为输入，func函数原型为def func(window, *series).
- 横截面算子 ==》ombinedCrossSectionalFactor(func, factors): 定义在 rqfactor.extension 中，其中 func 的原型为 func(dfs)

因子编写流程

根据上述理论以及米框对于因子的抽象，编写一个因子的时候，可以安装一下流程规范进行：
1> 解析因子逻辑,确定因子类型，调用合适的最外层算子
2> 按需求实现需要自定义的算子
3> 确定基础因子，使用UserDefinedLeafFactor类自定义系统中不提供的因子。
4> 根据基础因子实现简单复合因子。
5> 整合算子和因子，完成编写

举例

自定义基础因子

以仓单因子为例

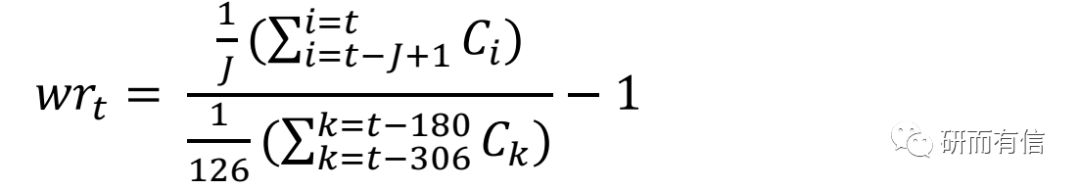
实现代码如下:

import re

def get_warehouse(order_book_ids, start_date, end_date):
    products = {re.match(r'[A-Za-z]+',code)[0]:code  for code in order_book_ids}
    wh = rqdatac.futures.get_warehouse_stocks(list(products.keys()),start_date,end_date)
    wh = wh[['on_warrant']].reset_index().pivot(index='date',columns='underlying_symbol',values='on_warrant')
    wh.index = pd.to_datetime(wh.index)
    wh = wh.rename(columns=products) 
    return wh

WAREHOUSE = UserDefinedLeafFactor('WAREHOUSE', get_warehouse)

wh_d10_d126 = MA(WAREHOUSE,10)/MA(REF(WAREHOUSE, 180),126)-1

滑动窗口因子

以如下因子为例，用5min交易数据来构建量价相关性因子。对于每个品种，t日的量价相关性因子采用以下方式构建：

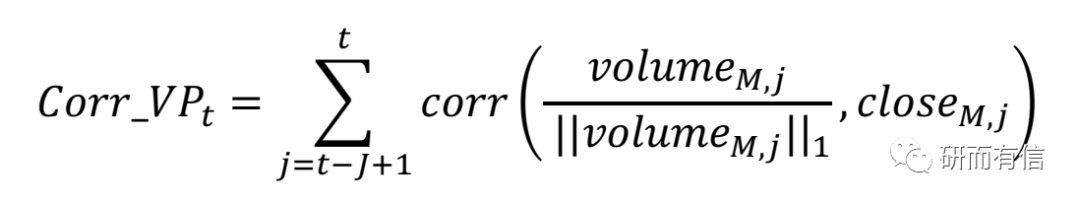
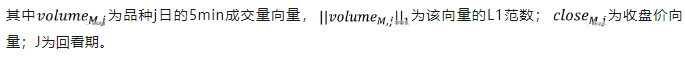
我们取j=21 得到日级别因子corr_vp_5m_d21

方案1
该因子需要计算21日的相关性之和，并且无截面操作
确定该因子为滑动窗口因子(SUM（factor_corr,21））

实现代码如下

def get_m5_vp(df):
    # data = pd.Series([3, -1, 4, 5, -2])
    l1_norm = np.linalg.norm(df['volume'], ord=1)
    a = df['volume']/l1_norm
    b = df['close']
    # 计算相关性系数
    correlation_matrix = np.corrcoef(a, b)
    # 获取 a 和 b 之间的相关性系数
    correlation_coefficient = correlation_matrix[0, 1]
    return correlation_coefficient

def get_day_corr_vp(order_book_ids, start_date, end_date):
    data = rqdatac.get_price(order_book_ids, start_date, end_date, fields=['volume','close'], frequency='5m', adjust_type='none',expect_df=True)
    # 考虑夜盘归属
    data['date'] = pd.to_datetime( data.index.get_level_values(1).date)
    data['night'] = (data.index.get_level_values(1).hour>20) | (data.index.get_level_values(1).hour<8)
    today = list(set(data['date']))
    today.sort()
    next_day = today[1:].copy()
    next_day.append(None)
    dict_next_trade_day = dict(zip(today,next_day))
    data['date'] =  data.apply(lambda x: dict_next_trade_day[x['date']] if x['night'] else x['date'], axis=1)
    df = data.groupby(['order_book_id','date']).apply(get_m5_vp ).reset_index().pivot('date','order_book_id')
    df.columns = df.columns.get_level_values(1)
    return df

DAY_CORR_VP = UserDefinedLeafFactor('DAY_CORR_VP', get_day_corr_vp)
corr_vp_5m_d21_v2 = SUM(DAY_CORR_VP,21)

方案2（单纯为了理解推荐使用方案一夜盘归属问题这个方案未修复）
确定该因子为滑动窗口因子(RollingWindowFactor）
其实5分钟的行情数据对于这个滑动窗口因子并不是基础因子，正真的基础因子是DATE，所以对DATE因子进行封装
把求和求相关性的过程放在RollingWindowFactor的转换方法中
实现代码如下

import rqdatac
from rqfactor.extension import UserDefinedLeafFactor,CombinedRollingWindowFactor
from rqalpha_plus.apis import *
rqdatac.init()

global corr_vp_5m_d21_codes
global corr_vp_5m_d21_executed_codes
corr_vp_5m_d21_codes = []
corr_vp_5m_d21_executed_codes = []

def get_date(order_book_ids, start_date, end_date):
    """
    可以考虑改按每个code去获取真实的交易时间
    """
    print("get_date")
    global corr_vp_5m_d21_codes
    corr_vp_5m_d21_codes = order_book_ids
    dates = rqdatac.get_trading_dates(start_date, end_date)
    data = [ MT_util_date_str2int(str(date)) for date in dates] 
    dict_data = {code:data for code in order_book_ids}
    df = pd.DataFrame(
        index=pd.to_datetime(dates),
        data=dict_data)
    # print(corr_vp_5m_d21_codes)
    # print(df)
    print("get_date finish")
    return df

# 做了些全局操作 所以这个因子 只给CORR_VP使用
DATE = UserDefinedLeafFactor('DATE', get_date)


def get_vp(df):
    # data = pd.Series([3, -1, 4, 5, -2])
    l1_norm = np.linalg.norm(df['volume'], ord=1)
    a = df['volume']/l1_norm
    b = df['close']
    # 计算相关性系数
    correlation_matrix = np.corrcoef(a, b)
    # 获取 a 和 b 之间的相关性系数
    correlation_coefficient = correlation_matrix[0, 1]
    return correlation_coefficient


# 每个code 都会调用一次 考虑自己维护code 避免重复计算
def rolling_corr_vp(f_date,window):
    print("rolling_corr_vp")
    global corr_vp_5m_d21_codes
    global corr_vp_5m_d21_executed_codes
    # 按window分组
    rolling_dates = rolling_window(f_date, window)
    # 获取tradedate
    #print(rolling_dates)   
    cal_code = None
    for code in corr_vp_5m_d21_codes:
        if code not in corr_vp_5m_d21_executed_codes:
            cal_code = code
            corr_vp_5m_d21_executed_codes.append(code)
            break
    vps = []
    if cal_code:
        for dates in rolling_dates:
            start_date = str(dates[0])
            end_date = str(dates[-1])
            # print(start_date,end_date)
            # 分别获取组内的5分钟数据
            print(cal_code)
            data = rqdatac.get_price(cal_code, start_date, end_date, fields=['volume','close'], frequency='5m', adjust_type='none',expect_df=False)
            if not data:
                print(f" rqdatac.get_price {cal_code} {start_date}-{end_date} 数据为空")
                vps.append(np.nan)
                continue
            data['date'] = data.index.date
            r = data.groupby('date').apply(get_vp)
            vp = sum(r)
            vps.append(vp)
    return vps

def CORR_VP(window):
    return RollingWindowFactor(rolling_corr_vp,window,DATE)

corr_vp_5m_d21 = CORR_VP(21)

展望

本节介绍完多因子理论,因子构造以及米框因子框架方面的基础知识，下一节开始，将深入期货多因子进行研究。

posted @ 2023-08-10 15:08 LazyTiming 阅读(479) 评论(0) 编辑收藏举报

刷新页面返回顶部

量化交易/机器学习/WPF/前后端技术爱好者