【数据结构】跳表(SkipList)代码实现之ConcurrentSkipListMap
承接【数据结构】跳表(SkipList)原理篇,本篇文章我们来分析下如何使用代码实现SkipList。在JDK中并没有SkipList的直接实现,当然我们可以自己写代码实现,但是为了给后面“一致性Hash算法”系列文章做铺垫,
这里我选择ConcurrentSkipListMap类来进行分析。
ConcurrentSkipListMap(Concurrent + SkipList + Map) ,正如它的名字一样,我们可以把它拆分成三个部分来看,它是一种线程安全的基于跳表实现的map数据结构。相对于简单的用代码实现 SkipList ,
ConcurrentSkipListMap 具有并发控制,一涉及到并发代码的复杂度就急剧增加。所以有部分代码比较晦涩、难懂,我们不需要特别关注这部分代码,只需要聚焦于 SkipList 实现的核心代码。另外 ConcurrentSkipListMap 类
提供了很多接口,解析所有接口实现就可以写一个系列文章,受篇幅原因本篇文章我们只分析 ConcurrentSkipListMap 的查询、添加、删除以及部分工具方法的实现。
ConcurrentSkipListMap 的实现是基于JDK1.8.0_271
1、SkipList 实现的三个核心类
ConcurrentSkipListMap 底层是使用跳表来实现数据的存储的,上一篇文章我们介绍了跳表结构的实现原理,ConcurrentSkipListMap 使用了三个内部类(Node、Index、HeadIndex)来维持跳表结构的构建,
分别对应着跳表结构中的数据节点、索引节点、头部索引节点,接下来我们先了解这三个内部类的设计。
需要特别提醒下,本片文章很多类只贴了和跳表实现紧密相关的代码,类的完整代码和提供的功能可以去看源码。
1.1、Node 类的设计
ConcurrentSkipListMap 是一个map数据结构,Node类是存储键值对数据的类,也是构成数据链的节点类,它除了拥有key和value两个分别表示键和值的成员属性外,还拥有一个成员变量next用于指向自己的后继节点;源码如下:
static final class Node<K,V> {
final K key; //键
volatile Object value; //值
volatile Node<K,V> next; //下一个节点的引用
//创建一个新的常规数据节点
Node(K key, Object value, Node<K,V> next) {
this.key = key;
this.value = value;
this.next = next;
}
//标记节点,和常规数据节点区别是它的key为null,value指向了自己
Node(Node<K,V> next) {
this.key = null; // key为空
this.value = this; // 值指向自己
this.next = next;
}
// CAS修改value为val
boolean casValue(Object cmp, Object val) {
return UNSAFE.compareAndSwapObject(this, valueOffset, cmp, val);
}
//CAS修改后继节点
boolean casNext(Node<K, V> cmp, Node<K, V> val) {
return UNSAFE.compareAndSwapObject(this, nextOffset, cmp, val);
}
//获取有效节点的值,防止取到头节点或标记节点
V getValidValue() {
Object v = value;
//标记节点、基础头节点不是有效的数据节点
if (v == this || v == BASE_HEADER)
return null;
// 否则返回value
return (V) v;
}
//......其他方法
}
在 ConcurrentSkipListMap 中定义了一个基础头节点,它也是一个 Node 实例,但其value被固定为常量 BASE_HEADER,Node 类提供了isBaseHeader()来判断节点是否是基础头节点。
所有的 HeadIndex 头索引节点指向的数据节点就是这种基础头结点。需要注意的是,Node类为value和next变量分别提供了CAS修改方法,保证在并发情景下对其修改过程的一致性。
getValidValue()方法则用于获取有效节点的值,规避基础头节点和标记节点这两类无效节点。
1.2、Index 类的设计
Index 类对应跳表中的索引节点,它包括一个指向Node类型的数据节点的引用,另外还包括两个Index类型的引用right、down,分别指向本层索引链的下一个索引节点和下层索引链中的索引节点。
static class Index<K, V> {
// 数据节点的引用
final Node<K, V> node;
// 右指针
volatile Index<K, V> right;
// 下层指针
final Index<K, V> down;
/**
* Creates index node with given values.
*/
Index(Node<K, V> node, Index<K, V> down, Index<K, V> right) {
this.node = node;
this.down = down;
this.right = right;
}
//其实就是链表的添加操作,使用CAS保证线程安全,该方法在索引层添加索引节点时会进行调用
final boolean link(Index<K, V> succ, Index<K, V> newSucc) {
Node<K, V> n = node;
newSucc.right = succ;
// n.value == null表示节点已经标记删除,这里直接返回false,外层调用的时候会进行重试。
return n.value != null && casRight(succ, newSucc);
}
//其实质就是链表的删除操作,使用CAS保证线程安全,这里同link()方法一样,已标记为删除的节点不进行后续操作。
final boolean unlink(Index<K, V> succ) {
return !indexesDeletedNode() && casRight(succ, succ.right);
}
}
Index 的结构是比较简单的,提供了casRight(Index<K, V>, Index<K, V>)方法来CAS方式修改right右指针的值;另外link(Index<K, V>, Index<K, V>)和unlink(Index<K, V>)分别用于插入、删除Index节点。
1.3、HeadIndex 类的设计
HeadIndex 继承自Index类,在其基础上扩展了属于自己的level成员变量,我们知道跳表需要维护索引的层数,这里的level字段就是存储的当前索引层是第几层,那么最顶层HeadIndex节点就记录了跳表当前最大索引层数。
/**
* Nodes heading each level keep track of their level.
* 继承自Index,并跟踪它自己的层级。
*/
static final class HeadIndex<K, V> extends Index<K, V> {
// 层级
final int level;
HeadIndex(Node<K, V> node, Index<K, V> down, Index<K, V> right, int level) {
super(node, down, right);
this.level = level;
}
}
ConcurrentSkipListMap 中有一个 private transient volatile HeadIndex<K,V> head; 字段指向着跳表最顶层的头索引节点。
2、ConcurrentSkipListMap 类的设计
第1小节中我们已经解析了跳表实现的三个核心类,那么
2.1、类变量和常量
挑了几个相关的类变量和常量如下:
//用于标识基本数据节点的特殊值
private static final Object BASE_HEADER = new Object();
/**
* The topmost head index of the skiplist.
* 指向跳表最高层级的头索引节点
*/
private transient volatile HeadIndex<K,V> head;
// 我们知道跳表是有序的,这个比较器就是map中用于key进行排序的,如果为null则默认使用自然排序
final Comparator<? super K> comparator;
//CAS方式更新head字段值
private boolean casHead(HeadIndex<K,V> cmp, HeadIndex<K,V> val) {
return UNSAFE.compareAndSwapObject(this, headOffset, cmp, val);
}
这些字段都比较简单,详细用途可以看注释,特别关注BASE_HEADER和head的意义。
2.2、构造方法
ConcurrentSkipListMap 总共有4个构造方法,这里只列出了默认、自定义比较器的构造方法,其他两个也比较简单可以看源码:
/**
* Constructs a new, empty map, sorted according to the
* {@linkplain Comparable natural ordering} of the keys.
* 默认构造方法,对key使用自然排序
*/
public ConcurrentSkipListMap() {
this.comparator = null;
initialize();
}
//自定义比较器
public ConcurrentSkipListMap(Comparator<? super K> comparator) {
this.comparator = comparator;
initialize();
}
/**
* Initializes or resets state. Needed by constructors, clone,
* clear, readObject. and ConcurrentSkipListSet.clone.
* (Note that comparator must be separately initialized.)
*/
private void initialize() {
keySet = null;
entrySet = null;
values = null;
descendingMap = null;
head = new HeadIndex<K,V>(new Node<K,V>(null, BASE_HEADER, null),null, null, 1);
}
四个构造方法中都调用了initialize()方法进行初始化,initialize()方法重置了一些与ConcurrentSkipListMap息息相关的成员变量。同时还初始化了head字段的引用,该字段是一个HeadIndex类型的实例,level级别为1,
right和down都为null,node字段指向new Node<K,V>(null, BASE_HEADER, null)该数据节点的value指向BASE_HEADER对象,这个对象在前面讲到过,就是一个简单的Object对象,仅用作标记使用。
2.3、调用 initialize() 方法后效果
文字很难描述 ConcurrentSkipListMap 调用 initialize() 方法后的效果,所以本节我们结合一个简单的例子以图形的方式来进行简单说明,如下图所示:
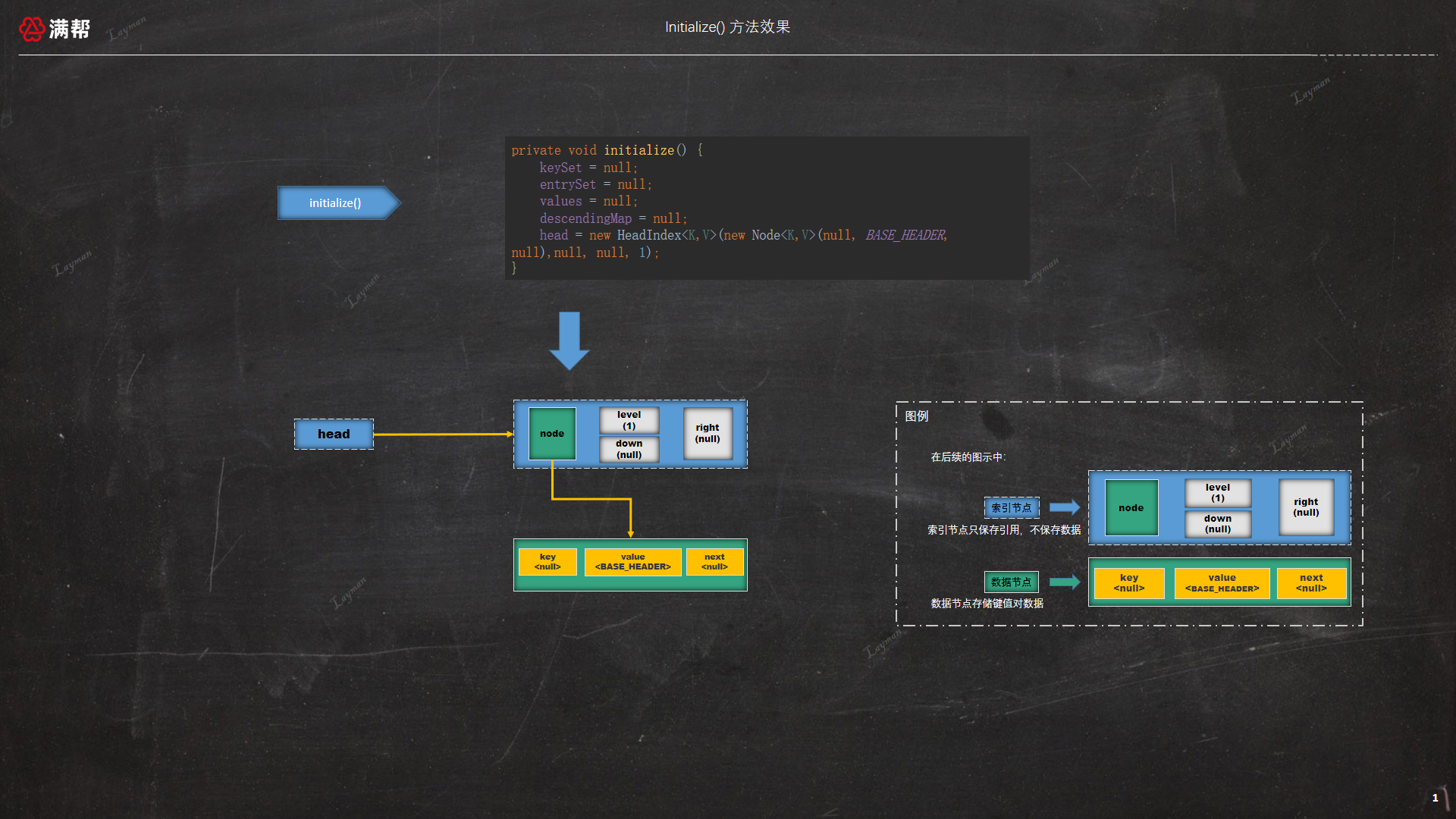
结合上一节的结论来看这张图
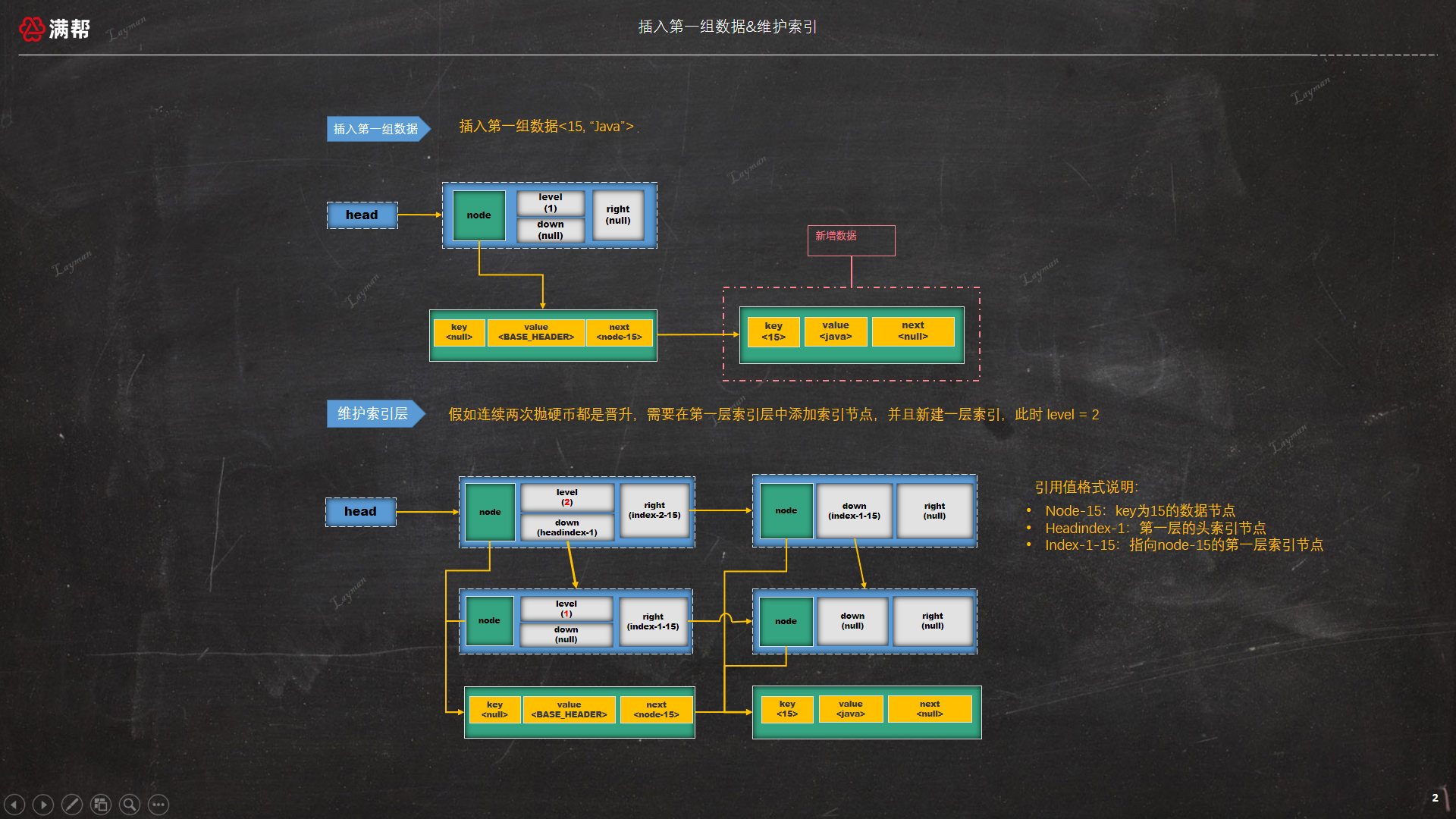
假如此时向map中添加两条数据 <15, "Java">、<20, "C++">,当成功将新数据<15,"Java">添加到跳表中后,会根据随机结果生成来维护跳表的级别结构。这里我们假设两次随机结果都是晋升,所以会创建两个Index节点,第二个Index节点的down指向第一个Index节点,
且两个Index节点的node都指向上面新创建的Node节点。因为需要新建索引层,所以需要创建一个level为2、down域指向head节点的HeadIndex节点;此时跳表中存在两个HeadIndex节点,需要将这两个HeadIndex节点的right域分别与两个Index节点相连接,并更新head成员变量,
使其指向新创建的level为2的HeadIndex节点。如图所示:
添加第二组数据的流程与上面的类似,不过这里需要抛硬币三次,因为当前level为2。假设三次随机结果同样都是晋升,因此也需要维护跳表的级别,添加第二组数据的示意图如下:
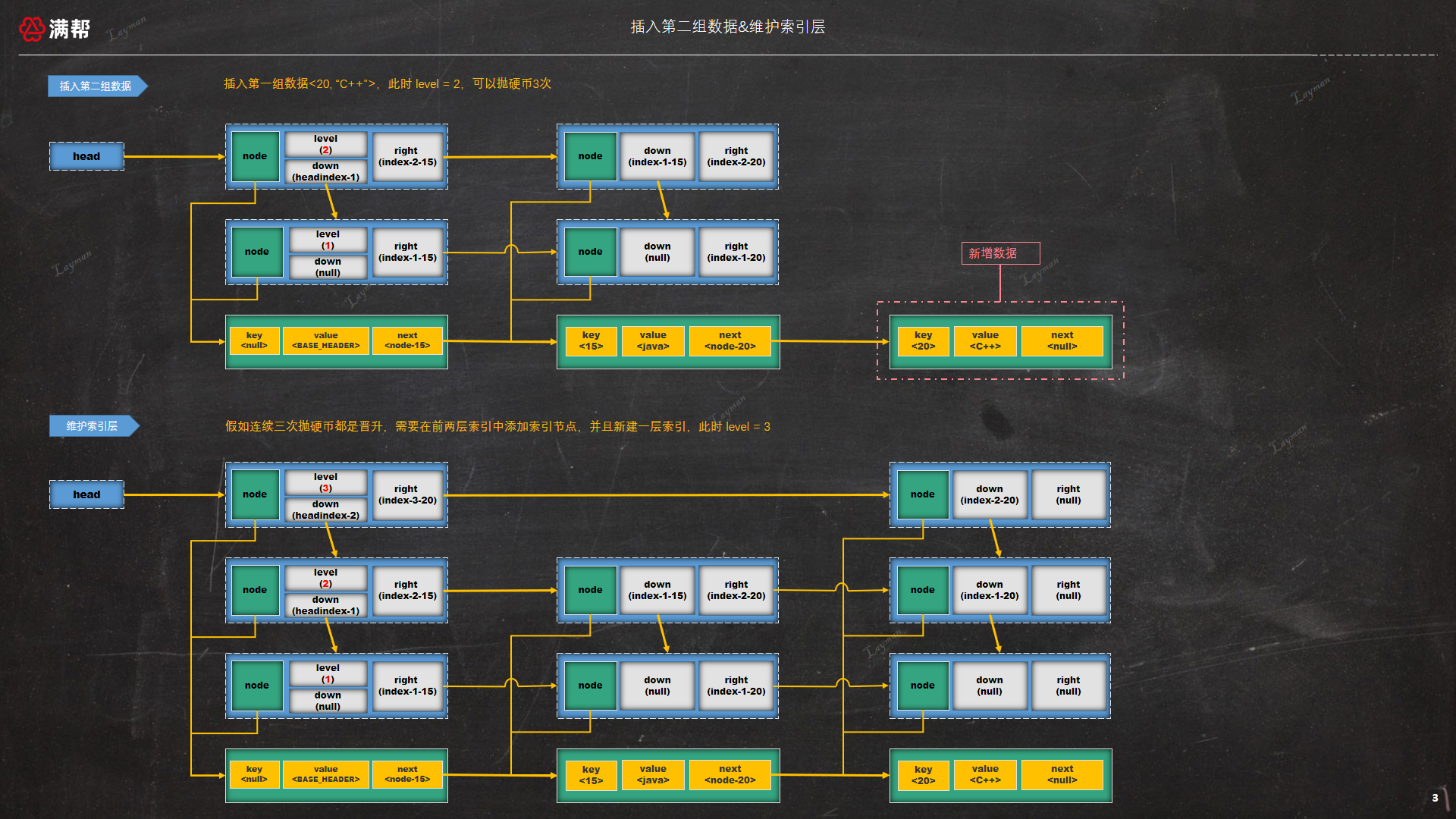
抛硬币这个动作实际用代码实现时并不会抛多次,仅仅只是产生一个
randomValue。当randomValue > level时,则level = level + 1表示需要新增一层索引并在所有索引层添加索引节点,
randomValue <= level时,需要在小于等于randomValue的索引层添加索引节点。
总结:根据以上的数据添加过程我们可以清晰知道
HeadIndex、Index、Node这三类节点在跳表中充当的角色,这也便于我们后面理解跳表的各类操作。
- Node 类:用于存储数据,同时拥有指向下一个数据节点的引用
volatile Node<K,V> next;构成跳表最底层的数据链- Index 类:索引节点的抽象,拥有指向数据节点的引用
final Node<K,V> node;,同时拥有指向其他索引节点的两个引用volatile Index<K,V> right;、final Index<K,V> down;用于维护跳表的索引层。- HeadIndex 类:头索引节点继承于Index类,其本身也是一个索引节点,区别在于这类型的节点存在于每层索引链的最开头,并且使用level字段维护着所处索引层是跳表的第几层。
- ConcurrentSkipListMap.head 变量:指向跳表最高层的头索引节点,跳表的数据检索都是从head指向的索引开始。
- ConcurrentSkipListMap的跳表结构中,第一列的索引节点都为
HeadIndex节点,从上往下进行衔接;除此之外其他列的索引节点都为Index节点。- 所有装载键值对的Node数据节点位于跳表结构的最底层,即每一列的最下面为
Node数据节点。- 每一列的Index节点的node变量都引用着这一列最下面的Node数据节点。第一列所有的HeadIndex节点的node变量引用的Node节点的值是BASE_HEADER节点,该Node代表基础头节点,并不存储有效数据。
- 每层的节点(无论是Node数据节点,还是HeadIndex和Index索引节点)都构成了一个单向链表结构。
3、跳表的实现
这一节我们将正式进入跳表具体实现细节,上一篇文章我们提过跳表的插入、删除都离不开查询,所以我们还是先解析查询代码的实现。由于ConcurrentSkipListMap中跳表结构的复杂性,
ConcurrentSkipListMap提供了大量的查找辅助方法,我们只解析其中最最重要的一个。
3.1、findPredecessor(Object key, Comparator<? super K> cmp) 辅助查询方法
我们知道跳表存储的数据是有序的,前面我们已经讲了ConcurrentSkipListMap中是根据key进行排序的,因此所有的键值对都是键有序的。当插入一组数据时首先需要找到在什么位置进行插入操作,此时就会调用findPredecessor()方法用于寻找给定键有效的前驱节点,该方法的源码如下:
/**
* Returns a base-level node with key strictly less than given key,
* or the base-level header if there is no such node. Also
* unlinks indexes to deleted nodes found along the way. Callers
* rely on this side-effect of clearing indices to deleted nodes.
* @param key the key
* @return a predecessor of key
*/
private Node<K,V> findPredecessor(Object key, Comparator<? super K> cmp) {
if (key == null)
throw new NullPointerException(); // don't postpone errors
for (;;) {
// 从head开始检索 --即从跳表最高层的头索引节点开始检索。
for (Index<K,V> q = head, r = q.right, d;;) {
if (r != null) { //头节点的右Index节点不为null
Node<K,V> n = r.node;
K k = n.key;
/**
* value为空表示这个Node节点已经被删除了(ConcurrentSkipListMap添加数据时value不能为null),就调用unlink()将其从链表中移除,unlink()操作会将q的右节点换成r的右节点,
* 移除不成功会跳出内层循环(有并发修改),否则继续往右边寻找索引节点。
*/
if (n.value == null) {
if (!q.unlink(r))
break; // restart
r = q.right; // reread r
continue;
}
// 走到这里说明value不为null,对比key比遍历到的节点的k大,就继续往后移,即将q指向r,将r指向r的右节点,然后继续下一次循环
if (cpr(cmp, key, k) > 0) {
q = r;
r = r.right;
continue;
}
}
/**
* 走到这里有两种情况:
* 1. r = null,此时表示q已经是该层最后一个索引节点,所以需要根据 q 的down指针下沉一层继续寻找。
* 2. r != null,但传入key <= 查找的k
* 注:r为q的后继节点
*/
if ((d = q.down) == null) //q.down 没有指向任何索引节点说明已经查找到了最一层索引层(可以回过头去看看示例),就直接返回了q.node指向的数据节点
return q.node;
//如果 q.down != null,则下沉到下一层索引层继续寻找
q = d;
r = d.right;
}
}
}
第一层for主要是为了有并发修改时跳出内循环然后重试,第二层for的内循环才是执行真正查找逻辑。
看代码是比较抽象难懂的,所以我们举个例子用图来解析说明下findPredecessor()是如何运行的。现在跳表中已经有两组数据:<15, "Java">和<20, "C++">,现在要插入一条新数据<17, "Python">,有以下是查找步骤:
3.1.1、首先从head这一层开始查找,最后会查找到<20, "Jack">,查找顺序如下:
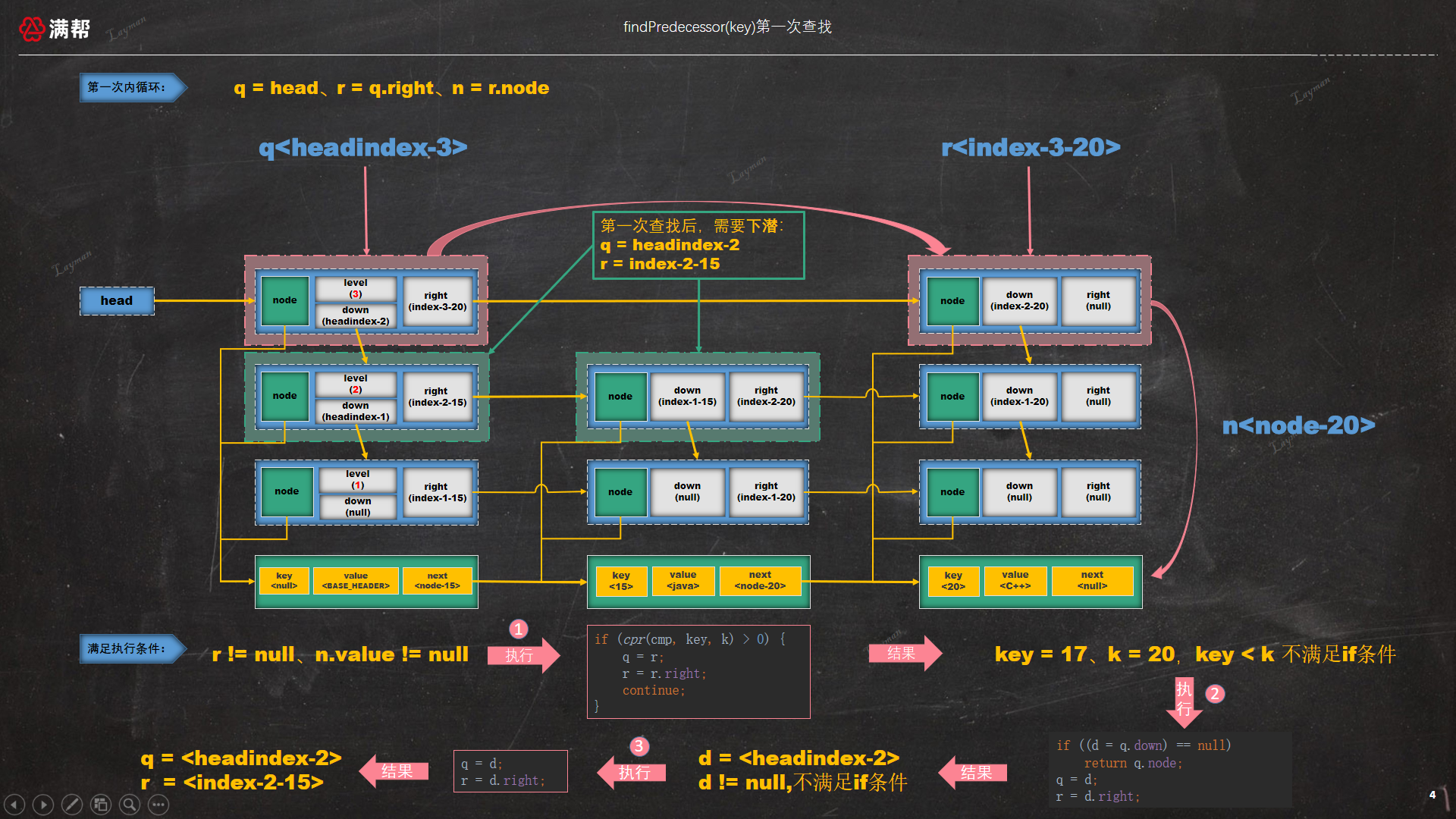
此时 key = 17比 index-3-20指定的数据节点 <20,C++> 的key小,所以需要下潜一层。
3.1.2、第一次下潜查找,最后会查找到<15, "Java">,查找顺序如下:
此时 key = 17比 index-2-15指定的数据节点 <15,Java> 的key大,需要往后移动继续查超。
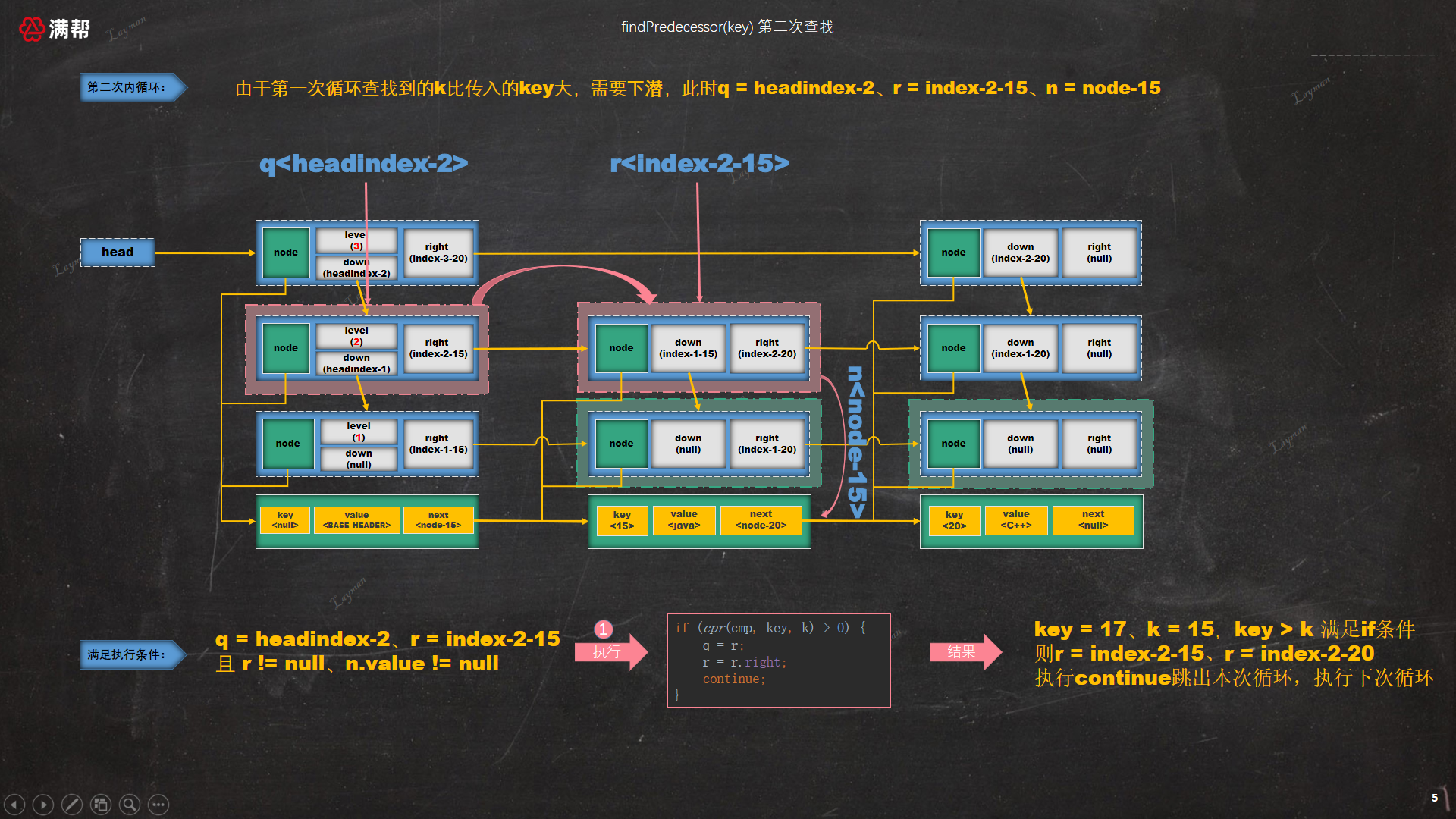
3.1.3、往后移动查找,最后又会查找到<20, "C++">,查找顺序如下:
此时 key = 17比 index-2-20指定的数据节点 <20,C++> 的key小,所以需要下潜一层。
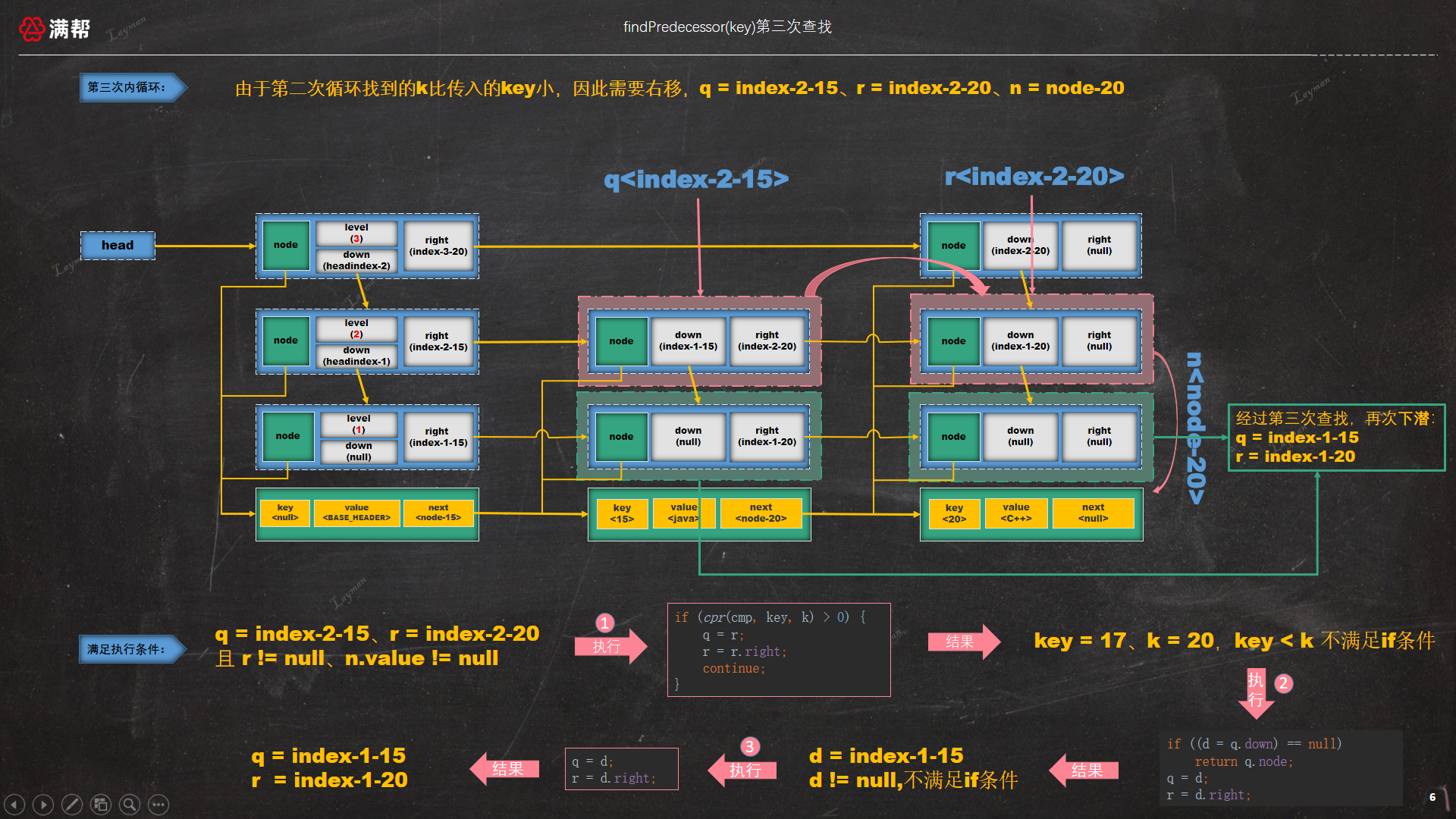
3.1.4、第二次下潜查找,最后还是会查找到<20, "C++">,查找顺序如下:
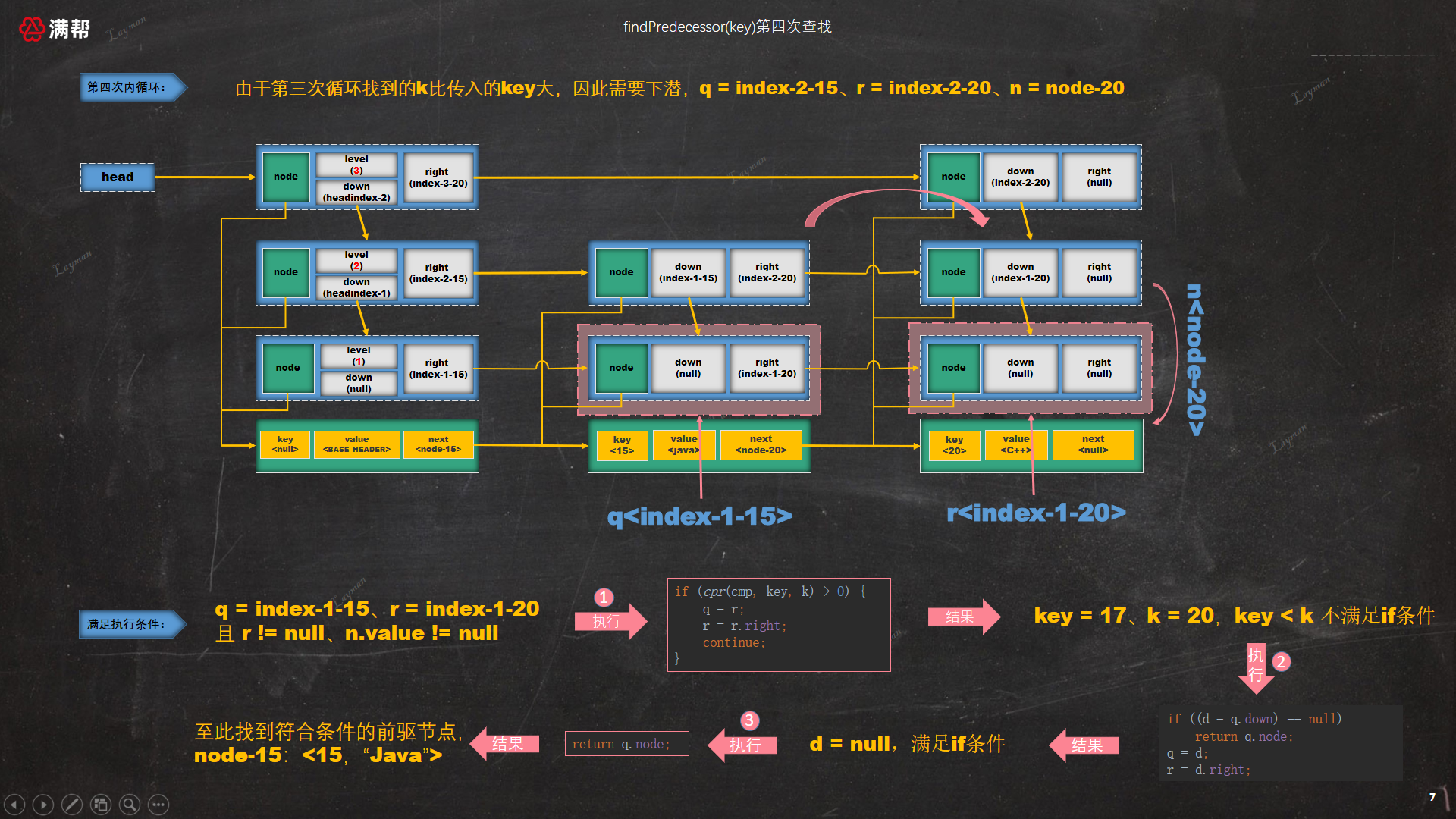
此时 key = 17比 index-2-20指定的数据节点 <20,C++> 的key小,需要继续下潜,但此时已无法下潜(由于q的down为null),因此q的node,即数据<15, "Java">节点即是符合条件的前驱节点。
总结:查找的规则在于从head开始查找,Node链中后面Node的key比前面的key要大, 因此查找时是从上往下,从前往后找
3.1.4、正确理解findPredecessor(Object key, Comparator<? super K> cmp)返回的Node
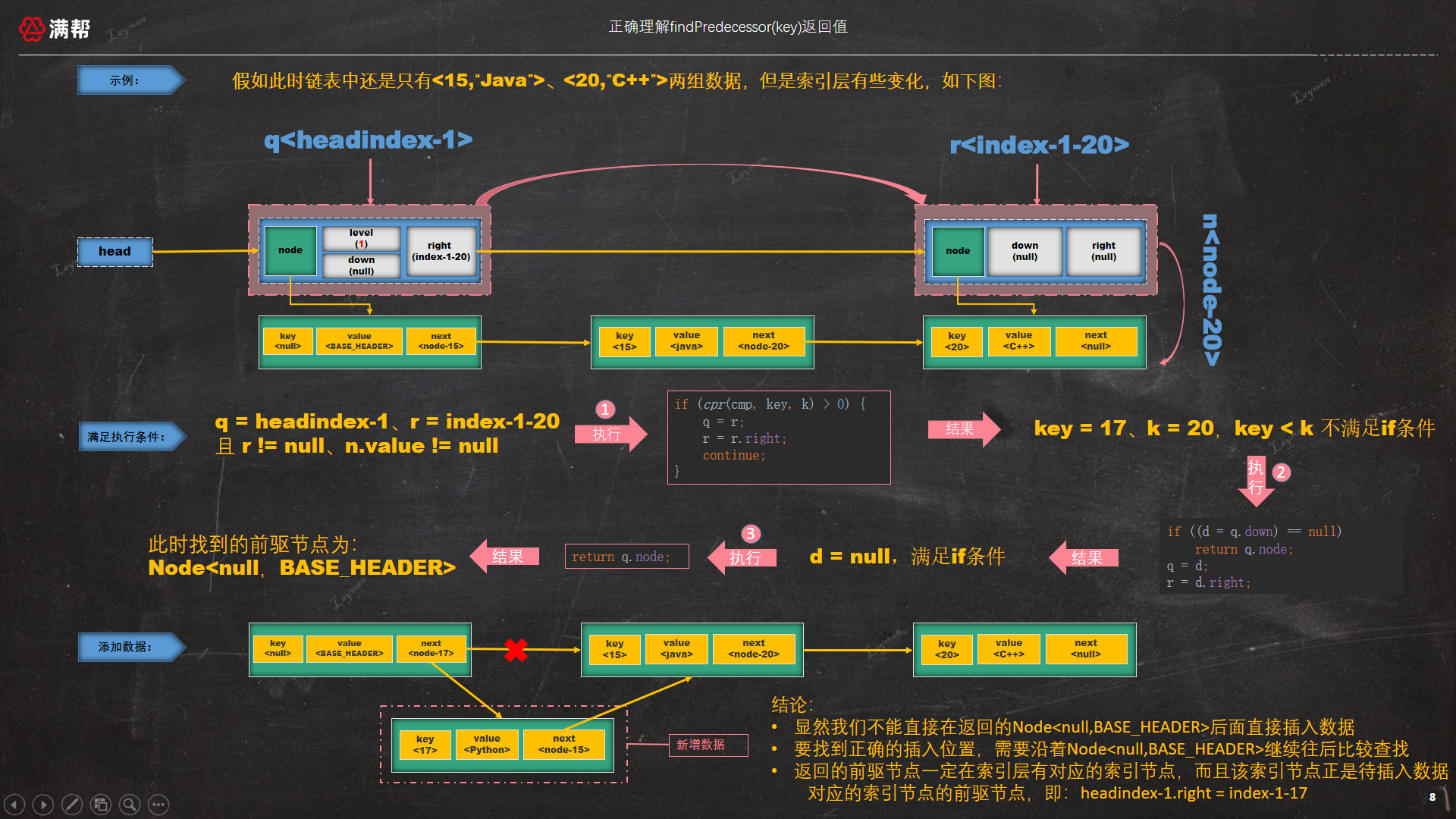
在3.1小节中我们对 findPredecessor(Object key, Comparator<? super K> cmp) 返回的 Node 节点加了两个重要的修饰词 有效的前驱节点,如何理解这两个词呢?
- 有效:node在当时一定是未删除的数据节点,对应到代码中 if (n.value == null) 做删除操作。
- 前驱节点:数据应该插入到返回的node右侧? 对应代码为:node.right = Node<17,"Python">,是否真的如此呢?我们在通过一个示例解析下:
![]()
OMG,和我们之前理解的完全不一样呢?链表中存储着相同的数据只是索引层不一致,这次返回的数据却是Node<null,BASE_HEADER>,具体结论在图示中说明了,这里不再赘述。
3.2、跳表的查找
前面花了很大的力气去解析findPredecessor(Object key, Comparator<? super K> cmp)的实现,当理解了实现后我们在看看跳表的查询就简单很多了,ConcurrentSkipListMap的查询实现如下:
public V get(Object key) {
return doGet(key);
}
private V doGet(Object key) {
if (key == null)
throw new NullPointerException();
Comparator<? super K> cmp = comparator;
outer: for (;;) {// 有并发操作时跳出内层循环然后进行重试
//findPredecessor(key, cmp) 根据key找到前驱节点,具体实现请看3.1小节,并且我们知道返回的b.key < key,还需要继续沿着b继续比较查找
for (Node<K,V> b = findPredecessor(key, cmp), n = b.next;;) {
Object v; int c;
//没有后继节点了,直接跳出完成循环,未找到等于key的node,返回null
if (n == null)
break outer;
// 此时 b -> n -> f
Node<K,V> f = n.next;
if (n != b.next) // inconsistent read 如果有并发操作修改了,跳出内层循环重新查找
break;
if ((v = n.value) == null) { // n is deleted n节点已经被删除,这里调用n.helpDelete(b, f)将n从链表中删除,然后重新查找
n.helpDelete(b, f);
break;
}
/**
* 走到这里存在两种情况:
* 1. v != null 且 v == n 说明n是标记节点
* 2. v != n,但b.value为null,说明b是被删除的节点
* 跳出内层循环
*/
if (b.value == null || v == n) // b is deleted
break;
// 如果n.key = key,说明找到了对应的数据节点,直接返回 n.value对应的数据
if ((c = cpr(cmp, key, n.key)) == 0) {
@SuppressWarnings("unchecked") V vv = (V)v;
return vv;
}
//此时 b.key < key < n.key,说明没有key对应是数据,直接跳出外层循环,返回null
if (c < 0)
break outer;
// 走到这里说明 n.key < key,需要继续右移查找
b = n;
n = f;
}
}
return null;
}
查找的代码实现总体来说还是比较简单的,只是 ConcurrentSkipListMap 是线程安全的,所以其中有很多状态检查,忽略这部分代码并不会影响我们对跳表查询的理解。也不进行图解了(画图很累的,嘤嘤~~~)。
3.3、跳表的插入
ConcurrentSkipListMap的put()相关的方法也有三类:put(K, V)、putIfAbsent(K, V)和putAll(Map<? extends K, ? extends V>)。底层都调用了doPut(K kkey, V value, boolean onlyIfAbsent)方法,区别在于传入的第三个参数不一样,
源码整个实现逻辑是比较长的,在上一篇文章中我们也提过跳表的插入其实分两部分,第一部分为向原始数据链表中插入数据、第二部分为为插入的数据维护索引。
3.3.1、向数据链表插入数据
doPut(K kkey, V value, boolean onlyIfAbsent)方法的第一部分源码如下:
private V doPut(K key, V value, boolean onlyIfAbsent) {
Node<K,V> z; // added node
if (key == null)
throw new NullPointerException();
Comparator<? super K> cmp = comparator;
outer: for (;;) {
//查找前驱节点,不再赘述
for (Node<K,V> b = findPredecessor(key, cmp), n = b.next;;) {
//第一类情况 n != null
if (n != null) {
Object v; int c;
// 此时引用顺序为: b -> n -> f
Node<K,V> f = n.next;
// 检查b的后继是否被改变,如果改变就跳出内层循环
if (n != b.next) // inconsistent read
break;
// n.value = null表示n已经被删掉了,将n从数据链表中删除后,跳出内层循环
if ((v = n.value) == null) { // n is deleted
n.helpDelete(b, f);
break;
}
/**
* 走到这里存在两种情况:
* 1. v != null 且 v == n 说明n是标记节点
* 2. v != n,但b.value为null,说明b是被删除的节点
* 跳出内层循环
*/
if (b.value == null || v == n) // b is deleted
break;
// 走到这里是第二类情况: key >= n.key:
// 当key > n.key,就往后移,跳出进行下一次循环,往右移继续查找。
if ((c = cpr(cmp, key, n.key)) > 0) {
b = n;
n = f;
continue;
}
// 当key = n.key,说明已经存在了数据,根据onlyIfAbsent参数进行覆盖或者直接返回旧值
if (c == 0) {
if (onlyIfAbsent || n.casValue(v, value)) {
@SuppressWarnings("unchecked") V vv = (V)v;
return vv;
}
//走到这里说明存在并发操作,替换值失败了,则跳出内循环重新执行插入操作
break; // restart if lost race to replace value
}
// else c < 0; fall through
}
/**
* 走到这里是第三类情况:,有两种情况:
* 1. n = null;此时b就是新节点的前驱节点
* 2. n != null且 key < n.key,因此n就是新节点的后继,b就是新节点的前驱
*/
// 构建一个新节点z,将n作为该节点的后继
z = new Node<K,V>(key, value, n);
// CAS方式在数据链表中插入新建的z节点,存在并发操作插入失败时,跳出内循环重新执行插入操作
if (!b.casNext(n, z))
break; // restart if lost race to append to b
// 插入成功,跳出最外层循环,完成数据插入操作
break outer;
}
}
//省略第二部分代码.....
}
3.3.2、图解数据插入
我们接着3.1节的示例,插入一条新数据<17, "Python">时根据 findPredecessor()方法查找到前驱节点 Node<15,"Java">,然后插入数据Node<17,"Python">,如图所示:
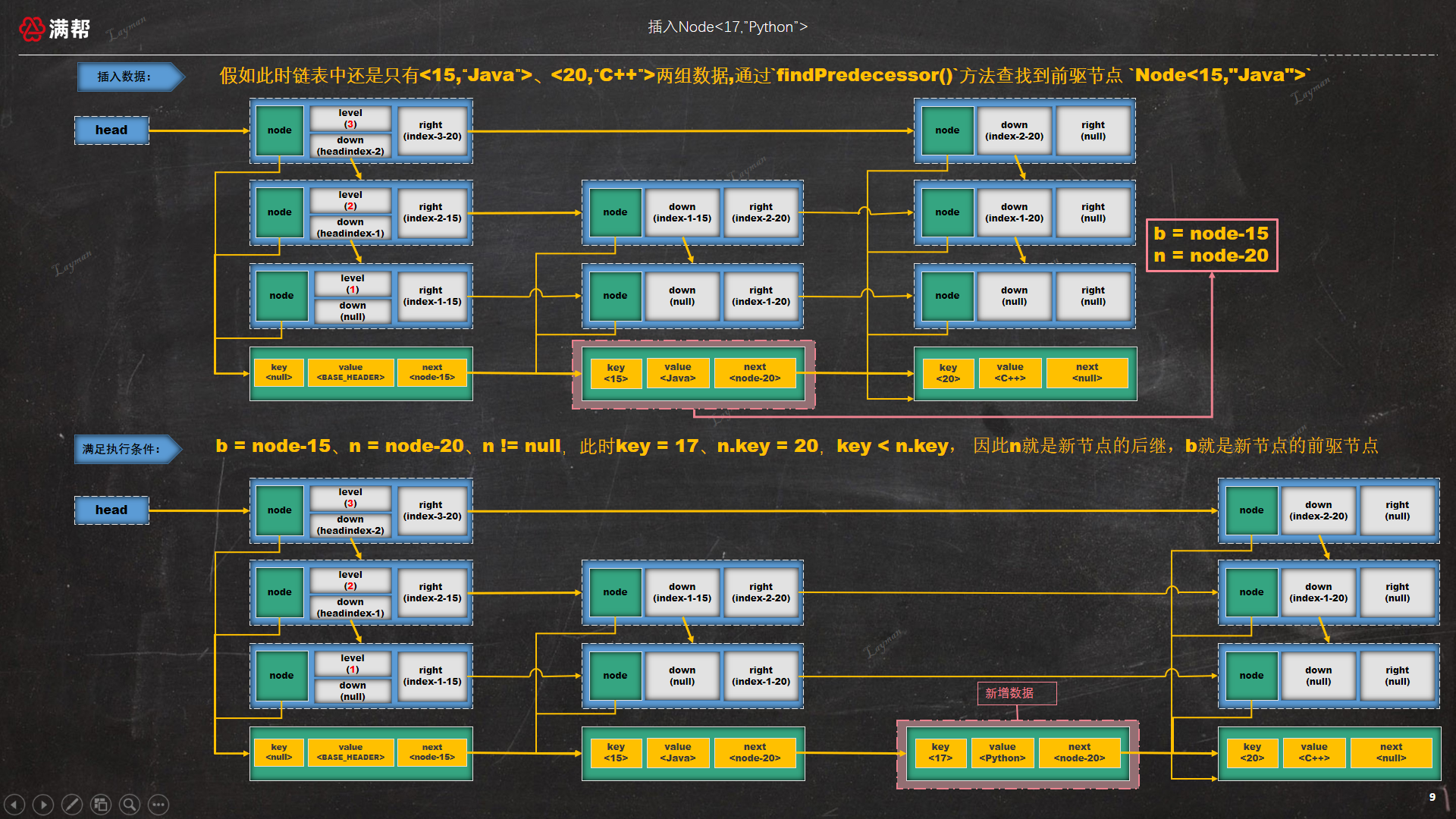
- 特别需要注意下键值比较时
// key > n.key,就往后移,跳出进行下一次循环,往右移继续查找:
if ((c = cpr(cmp, key, n.key)) > 0) {
b = n;
n = f;
continue;
}
注:这种情况是存在的,比如<15, "Java">和<20, "C++">中间还存在其他的数据,例如<16, "Ruby">时,我们还需要继续往右移进行查找比较,一直往右移动到n被置为null时,第一类情况会在下一次内层循环转换为第三类情况。
3.3.3、维护索引层
当插入一个新的Node节点成功后,需要根据新创建的Node节点z和随机得到的级别向跳表中插入了对应的Index节点,代码如下:
private V doPut(K key, V value, boolean onlyIfAbsent) {
//省略第一部分插入数据代码....
//生成一个随机数
int rnd = ThreadLocalRandom.nextSecondarySeed();
if ((rnd & 0x80000001) == 0) { // test highest and lowest bits
int level = 1, max;
//根据生成的随机数,每次无符号右移1位(实质就是除以2) 为奇数表示晋升level + 1,最后level的值就是需要添加索引的节点数
while (((rnd >>>= 1) & 1) != 0)
++level;
// idx引用着需要添加的索引列最上层的索引节点。
Index<K,V> idx = null;
HeadIndex<K,V> h = head;
//当随机层级小于当前索引最大层数时,创建level对应数值的索引列,最后创建的索引节点在最上层。
if (level <= (max = h.level)) {
for (int i = 1; i <= level; ++i)
idx = new Index<K,V>(z, idx, null);
}
//当随机层级大于当前索引最大层数时,需要新建一层索引层,所以level = 当前索引层数 + 1
else { // try to grow by one level
level = max + 1; // hold in array and later pick the one to use
@SuppressWarnings("unchecked")Index<K,V>[] idxs =
(Index<K,V>[])new Index<?,?>[level+1];
//创建level对应数值的索引节点并关联,最后创建的索引节点在最上层,并且使用数组idxs[]存储着创建的索引节点,数组的角标就对应着索引的层级,主要是便于在索引层插入索引节点时获取索引节点。
for (int i = 1; i <= level; ++i)
idxs[i] = idx = new Index<K,V>(z, idx, null);
//下面这段代码就是新建一层索引层,即创建一个HeadIndex索引节点,并修改head指向新建的HeadIndex
for (;;) {
h = head;
int oldLevel = h.level;
//level <= h.level,说明存在并发情况,已经有线程新建了一层索引,这个时候就没有必要新建索引层了,就回到了上面 if (level <= (max = h.level))的情况,此时已经创建好了需要添加的索引节点,所以直接调出循环往下执行添加索引节点到索引层。
if (level <= oldLevel) // lost race to add level
break;
HeadIndex<K,V> newh = h;
Node<K,V> oldbase = h.node;
//这里使用for循环创建,还是并发的问题,有可能一个线程已经删除了一层索引,那么这里就需要创建两层索引。
for (int j = oldLevel+1; j <= level; ++j)
newh = new HeadIndex<K,V>(oldbase, newh, idxs[j], j);
//最后CAS修改head的引用,修改失败的话说明存在并发,此时跳出循环不修改head的引用,往下执行添加新建的索引节点到索引层。
if (casHead(h, newh)) {
h = newh;
idx = idxs[level = oldLevel];
break;
}
}
}
// 从这里开始就是插入索引节点的具体逻辑,需要找到新建索的引节点在对应索引层的位置,并且插入到索引链表中。
splice: for (int insertionLevel = level;;) {
// 当前索引层数
int j = h.level;
// 从 int insertionLevel = level、q =head 、q = q.down可以看出,是从最上层索引层从上往下开始插入索引节点。
for (Index<K,V> q = h, r = q.right, t = idx;;) {
//q == null 说明没有索引层、t == null 说明没有需要添加的索引列,所以直接跳出最外层循环完成插入操作。
if (q == null || t == null)
break splice;
// 头索引节点指向的后继索引节点不为null
if (r != null) {
Node<K,V> n = r.node;
// compare before deletion check avoids needing recheck
// 比较新插入数据key 和 r.node.key的大小,主要是查找插入索引的位置。
int c = cpr(cmp, key, n.key);
// 如果n.value == null 说明n指向的数据节点已经标记为删除,所以需要调用 q.unlink(r) 方法将 r指向的索引节点从索引层中删除(就是将q.right = r.right)。
if (n.value == null) {
//删除索引节点失败,说明存在并发删除的情况,所以跳出内层循环,从新执行插入索引操作。
if (!q.unlink(r))
break;
//执行到这里说明删除索引节点成功,r被重新赋值继续执行查找插入位置(此时 r = (old r).right)
r = q.right;
continue;
}
// 如果插入数据的key比当前查找的索引节点r指向数据的key大,则往右移继续查找。
if (c > 0) {
q = r;
r = r.right;
continue;
}
}
/**
* 走到这里,说明待插入Index节点的node的key小于或等于r节点的node的key,即已经找到了Index节点正确的待插入位置。
* j == insertionLevel,insertionLevel 记录了待插入Index节点的级别,j记录了q与r的级别,所以这里是判断当前待插入Index节点的级别与q与r的级别是否相同,为了保持索引从低层层到高层是连续的(索引一定是从第一层开始往上的)。
* 如果相同则可以插入,如果不同,应该在当前层的下面层进行尝试插入,
* 以保持插入节点后Index列的高度与HeadIndex列的高度保持低部对齐
*/
if (j == insertionLevel) {
/**
* 走到这里说明层级是相同的,所以直接插入索引节点:
* 1、如果插入成功:此时q.right -> t、t.right -> r
* 2、如果插入失败:说明存在并发操作,跳出内层循环重新从head开始查找插入位置执行插入索引节点操作。
*/
if (!q.link(r, t))
break; // restart
//t.node.value == null 说明刚才插入的数据被删除了,这里调用了findNode(key)方法其作用是将被标记为删除的node从底层数据链表中删除。特别需要注意的是这里并没有删除刚插入的索引节点,这就回到if (n.value == null)的判断逻辑从而删除索引节点。
if (t.node.value == null) {
findNode(key);
break splice;
}
//--insertionLevel == 0 说明新建的索引列已经全部插入到了对应索引层中,所以跳出外循环完成整个数据插入操作。
if (--insertionLevel == 0)
break splice;
}
/**
* 走到这里,有两种情况:
* 1. 尝试插入Index时,发现待插入Index节点与q与r不在同一个层级,为了保持索引从底层到高层是连续的,因此需要下潜一层再尝试插入。
* 2. Index插入成功了,但insertionLevel自减后还不为0,即表示插入的Index其实是一个多层的列,还剩余有层级没有进行连接处理。
*/
if (--j >= insertionLevel && j < level)
// t指向新建索引列从上往下的下一个待插入索引节点
t = t.down;
//下潜索引层,需要在下层插入索引节点
q = q.down;
r = q.right;
}
}
}
}
维护索引层的代码还是可以分为两个小部分,第一部分是随机一个层级(对应代码中level)并根据随机的数值创建一个索引列(对应代码中idx),第二部分根据level和idx逐级维护跳表与待添加的Index节点间的层级关系。
3.3.4、图解创建索引列
为了更好的说明第一部分索引列的创建,我们用图示来进行说明,假如随机层数 level = 2 此时需要创建拥有两个索引节点的索引列,如下:
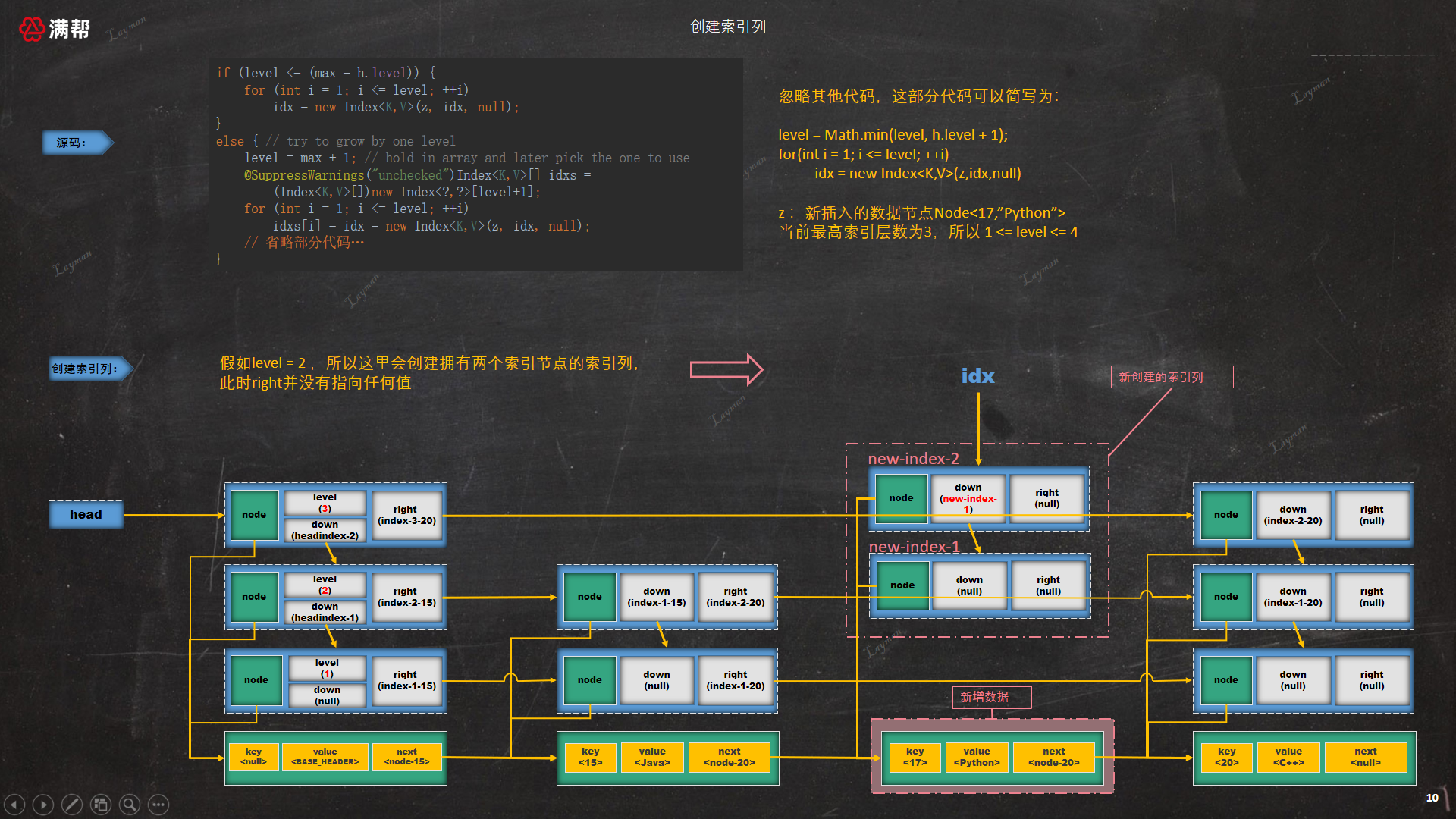
3.3.5、插入索引节点
此时跳表的索引层数 h.level = 3,随机层级数 level = 2 并创建好了索引列,此时流程走到第二部分向索引层插入索引节点,查找插入位置是从头结点开始,即从上到下、从左到右。
3.3.5.1、第一次查找索引插入位置
因为新创建的索引列只有两个索引节点,当前跳表的索引层数为3,为了保持新建的索引列同headindex索引列底部对齐,那么新创建的两个索引节点应该分别插入到第一层索引层、第二层索引层。
查找插入索引位置是从最高层的头索引节点开始查找,第一查询肯定不满足底部对齐条件,需要下潜,如图所示:
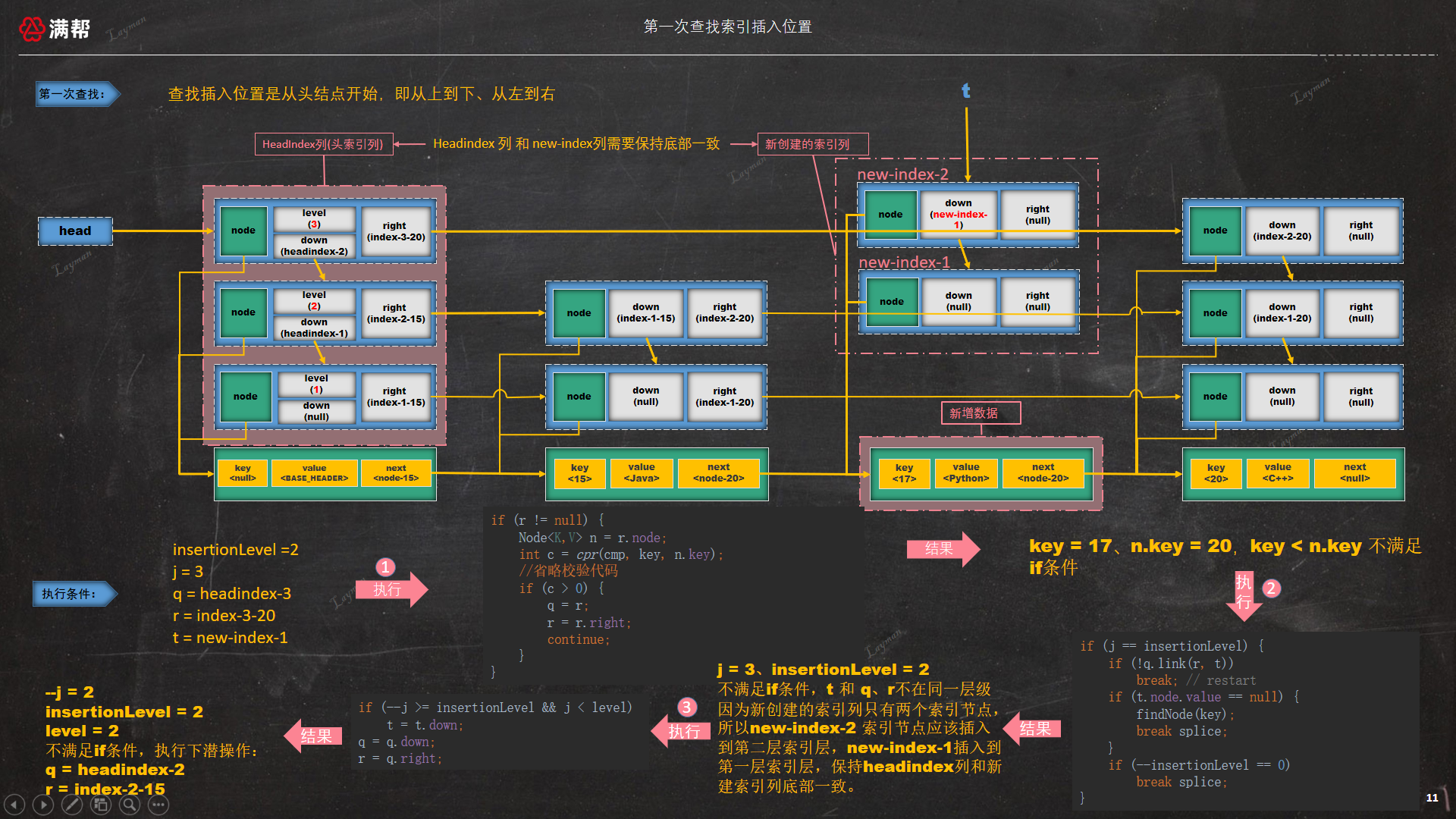
3.3.5.2、第二次查找索引插入位置
第一次查找时因为不满足底部对齐条件而进行了下潜,此时 q = headindex-2、r = index-2-15,第二次查询将从 headindex-2头索引节点开始查找,此时查找的n.key = 15 < key = 17需要继续右移查找,如图所示:
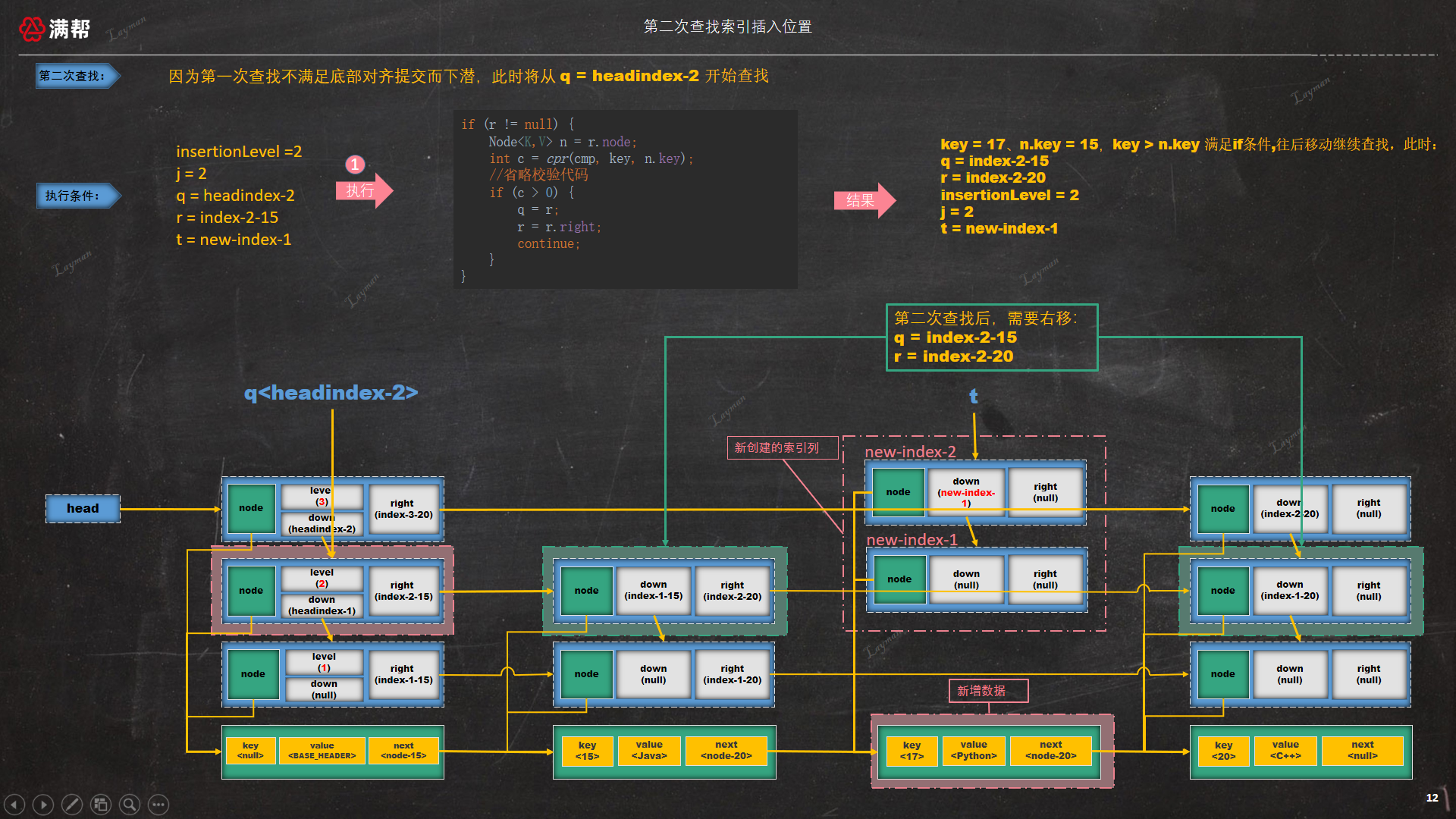
3.3.5.3、第三次查找索引插入位置
第二次查找右移后q = index-2-15、r = index-2-20不满足右移条件,继续往下执行进行 if (j == insertionLevel),此时j = 2、insertionLevel = 2 满足底部对齐条件进行索引节点插入,如图所示:
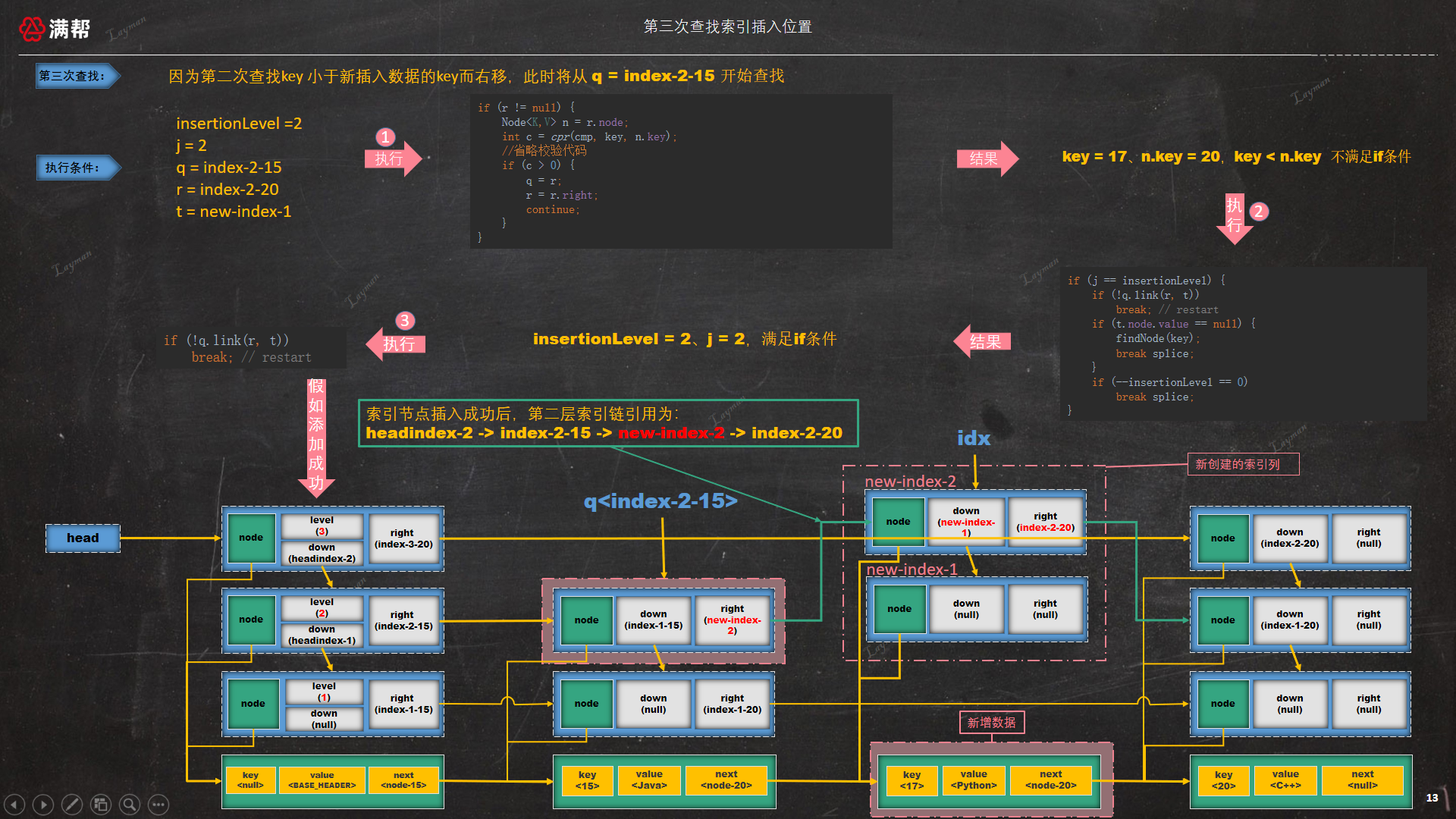
执行了插入索引节点后会继续执行如下代码:
if (j == insertionLevel) {
if (!q.link(r, t))
break; // restart
if (t.node.value == null) {
findNode(key);
break splice;
}
if (--insertionLevel == 0)
break splice;
}
if (--j >= insertionLevel && j < level)
t = t.down;
q = q.down;
r = q.right;
此时 --insertionLevel = 1 不满足if条件不会跳出外层循环,--j = 1、level = 2 满足 if (--j >= insertionLevel && j < level) 条件,此时 t = t.down -> new-index-1,然后继续下潜操作 q = index-1-15、r = index-1-20进行下一次查找。
3.3.5.4、第四次查找索引位置
在第三次查找到正确位置并插入new-index-2后进行了下潜操作,此时q = index-1-15、r = index-1-20进行第四次查找基本和第三次查找是一样的逻辑,会在第一层索引层 index-1-15后面插入new-index-1。
此时 --insertionLevel = 0 满足 if (--insertionLevel == 0)条件将会直接跳出最外层循环结束整个插入数据的操作,最终跳表的结构如图所示:
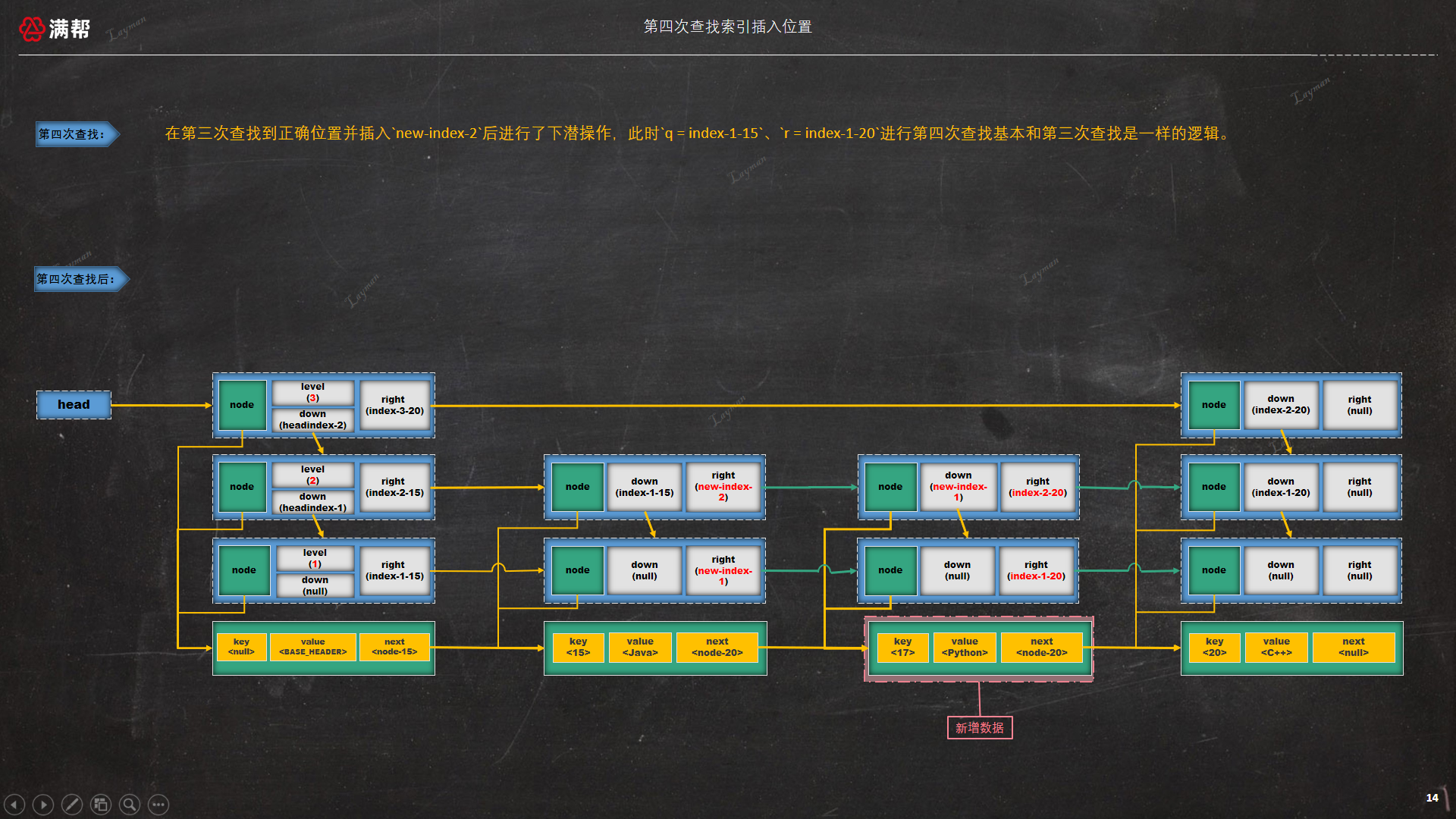
总结:从上面的分析可知,doPut(K kkey, V value, boolean onlyIfAbsent)方法的实现的确非常复杂,其实主要复杂的地方并不是新键值对的添加,而是对整个跳表结构的维护。只需要明白以下的两个注意点即可:
- 在ConcurrentSkipListMap添加键值对时,会首先找到符合条件的前驱Node节点,然后将键值对包装为Node节点,添加时需要继续对找到的前驱节点进行后续比较然后插入。
- 每次添加之后会随机得到一个级别,如果级别大于0,就会构建相应数量的Index节点构成Index列,插入到跳表中。维护索引的层级相对来说比较复杂,需要结合图示慢慢理解。
3.4、跳表的删除
在3.3、跳表的插入小节详细介绍了向跳表插入数据和维护索引层,在理解了跳表的插入操作后再来看跳表的删除已经不是那么困难了。ConcurrentSkipListMap针对删除操作提供了两个重载方法:remove(Object key)和remove(Object key, Object value),
两个方法内部最终都调用doRemove(Object okey, Object value)方法 源码如下:
final V doRemove(Object key, Object value) {
if (key == null)
throw new NullPointerException();
Comparator<? super K> cmp = comparator;
outer: for (;;) {
// 依然是熟悉的味道,findPredecessor(key, cmp) 根据key找到前驱节点
for (Node<K,V> b = findPredecessor(key, cmp), n = b.next;;) {
Object v; int c;
// 因为b是前驱节点,待删除的数据一定在b之后,n为null,表示要删除的节点不存在,直接返回null。
if (n == null)
break outer;
Node<K,V> f = n.next;
// 检查b的后继是否被改变,如果改变就跳出内层循环(针对并发的检查)。
if (n != b.next) // inconsistent read
break;
// n.value == null,表示n已经被删掉了,所以调用 n.helpDelete(b, f) 将索引节点n从索引层中删除掉。
if ((v = n.value) == null) { // n is deleted
n.helpDelete(b, f);
break;
}
/**
* 两种情况,都需要跳出内层循环:
* 1. v == n说明n是标记节点
* 2. v != n,但b.value为null,说明b是被删除的节点
*/
if (b.value == null || v == n) // b is deleted
break;
//(c = cpr(cmp, key, n.key)) < 0,表示 b.node.key < key < n.node.key,但是 b.right = r ,这种情况下key所对应的节点是不存在的.
if ((c = cpr(cmp, key, n.key)) < 0)
break outer;
/**
* 要比n的key大,就往后移,跳出进行下一次循环,即往后遍历:
* 之前:b -> n -> f
* 现在:(old b) -> b(old n) -> n(old f)
*/
if (c > 0) {
b = n;
n = f;
continue;
}
//走到这里说明比较结果c == 0,即找到了key对应的节点,!value.equals(v) 是针对传入了value参数的情况,只有传入的value和找到的节点的value相同才会继续往下走,否则视为没有找到节点,返回null
if (value != null && !value.equals(v))
break outer;
// CAS方式修改n的value为null,修改不成功就跳出内层循环,进行下一次尝试
if (!n.casValue(v, null))
break;
/**
* 当前结构为:b -> n -> f
* 跳过n节点,即:
* n.appendMarker(f)的作用后:b -> n -> marker -> f,即新建一个标记节点,f作为该标记节点的后继节点,然后将该标记节点作为n的后继节点
* b.casNext(n, f)的作用后:b -> f,即把f作为b的后继节点,跳过n
*
* n.appendMarker(f)成功后才会执行b.casNext(n, f),如果两步有一步失败,就会执行findNode(key)进行重试,findNode(key)方法会移除刚才标记为删除的节点。
*/
if (!n.appendMarker(f) || !b.casNext(n, f))
findNode(key); // retry via findNode
else {
// 走到这里说明if代码块中的两步都成功了,利用findPredecessor函数的副作用,删除n结点对应的Index结点(我们在findPredecessor方法中看到的n.value == null的判断)。
findPredecessor(key, cmp); // clean index
// 头结点的right == null,表示头节点这一层只有head一个节点,所以需要减少层级
if (head.right == null)
tryReduceLevel();
}
// 返回删除的旧值
@SuppressWarnings("unchecked") V vv = (V)v;
return vv;
}
}
return null;
}
上面对doRemove(Object, Object)方法的文档注释已经阐明了它的删除原理,即:定位Node节点、将其值置为null、添加删除标记节点,将其从前驱节点上断开连接,移除辅助索引节点,还有可能会减少HeadIndex的层级。虽然操作步骤多,但是每一步操作还是比较简单的,这里就不在进行图解了。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号