Since01-11(119)
2017-01-10 周二(72)
▲18:26:53 UOJ130 荷马史诗(NOI2015) 哈弗曼树/优先队列:得到最优解的方法:先把每个点作为大小为1的树,每次从所有树里选择两个权值最小的合并成一个树.直到最后只剩下一棵树.为了维护最长长度最小,只要让优先队列维护两维,一是权值,二是长度,每次在相同权值里选长度较小者.对于K叉树,方法同理,只要每次选K个合并成一棵树.注意,这里就有可能最后可选元素不到K的的情况,此时只要把初始元素补上,权值设为0即可.
2017-01-11周三(74)
▲10:17:25 UOJ132 小园丁与老司机(NOI2015)[请允许我吐槽一下这个标题233] DP+网络流 DP:把点根据y排序,不同行的可以直接转移,同行的需要用前缀和维护最值,处理出f[i]和dp[i]分别表示从i出发能走到的最多的点数和走到i经历最多点数.这样可以完成第一问.输出方案需要记录每个节点的f值的转移来源即可. 求出dp和f就可以确定任意一条非左右边是否可能经过.找到这些边再重新构成一个DAG.第三问就是个坑!!不过我的瞎搞也得了97分很满意233!!现在说正解把..如果最后压路机不能经过重复的边,那么最后答案是sum{max(in[i]-out[i],0)}.但由于可以重复经过某些边,相当于可以再图中加入重边(u,v),如果out[u]<in[u]&&in[v]<out[v],那么答案就会-1.只要把所有in>out的点与S连一条流量为in-out的边,所有out>in的点与T连一条out-in的边,DAG中的其他边流量为oo,那么最后S到T的最大流就是加入的重边对答案的减小量.
▲22:30:33 UOJ110 Bali Sculptures(APIO2015) 按位贪心+DP 遇到balabalabala..然后求几个数按位或运算的值最大/最小时,可以想按位考虑,贪心啊二分啊什么都可以搞了.
2017-01-12周四(76)
▲18:28:18 UOJ111 Jakarta Skyscrapers(APIO2015) 分块决策/BFS/最短路 经过分析可以看出就是求两点之间的最短路.朴素方案边数为n*m,可以得57分.正解当然没有这么简单..(但也挺简单的233),即分类决策.当P很大时,每个点可以到的点是有限的,而当P较小时,每个点之间互相到达就更容易,我们可以以此来状态压缩判重,和BFS. BFS中的某个状态可以这样来描述:当前的doge所在位置为pos,走过来的步长为p,方向是f,已经走了step步.对于当前状态,我们有两个方向来延伸出新状态,第一是继续沿着当前的方向走,也就是同一只doge继续走;第二是让pos所在的doge出发.我们可以确定延伸状态的对应信息,但是如何判重.
对于第二种情况,如果nex点已经被触发,那么是不必再更新的.我们把步长较小的状态进行判重,假如当前位置pos,走到pos的步长为p,那么(pos,p)就是判重的信息了,而不用考虑方向,因为假如能得到状态(pos,p)那么一定是从pos-p或者pos+p得到的,那么无论当前pos往前还是往后都有对应的最优解,不必考虑方向.
对于p这种关键词->每次跳的步长为p,每次走p,p的倍数等等等,都可以想想分类决策!!青蛙跳!!!
▲20:37:24 UOJ112 Palembang Bridges(APIO2015) 【神题加亮】推结论/终态枚举/权值线段树 这道题妙啊!!!
首先考虑当K=1时,答案就是sum{abs(x-c)+abs(y-c)},c是桥的位置,可以发现最后答案的x,y的组合是无关的!!可以把x,y放在一个序列里,排序,问题就相当于找到一个c使得大于c的每个数和c的差加上小于c的每个数和c的差的总和最小->这是个经典问题,最优解c就是这个序列的中位数.
那K=1就相当于求一个序列的中位数.
K=2时,现在有两座桥,设为c<d.对于b<=c和a>=d的两类的决策是显然的.对于a<=c<=b或者 a<=d<=b,答案就是b-a.那么还剩下一类是c<a<=b<d的, 假设选择c更优,就有 a+b-2*c<2*d-(a+b) => 2(a+b)<2(c+d). =>mid(a,b)<mid(c,d)
那就可以得到一个结论,对于Mid(a,b) 小于Mid(c,d)的所有点都应该走c,其余走d.那如果按照mid(a,b)给每个点排序,就可以枚举所有可能的方案:[1,i]走c,[i+1,n]走d.那么就把问题转化为了K=1的情况,也就是求中位数了.只要维护一棵权值线段树支持查询第K小值和单点更新即可.
太神了!!
2017-01-13周五(78)
▲18:22:07 BZOJ4562 食物链(HAOI2016) 拓扑排序搞一下/注意可能有的点不在某条边上!!
▲19:16:20 BZOJ4566 找相同子串(HAOI2016) 后缀自动机 利用其得到的树形结构 递推一下
-----------------------------------------------------------------这里是严肃的分界线--------------------------------------------------------------
2017-01-24 周二(80)
▲16:45:27 BZOJ4563 放棋子(HAOI2016) 错排公式+高精
▲21:34:01 BZOJ4565 字符合并(HAOI2016) 区间DP 序列最后剩下的长度一定<m,所以可以用一个二进制数来表示一个区间最后合并的结果.假设g[i][j][k]为区间[i,j]合并为k的最大值,那么可以通过前推式DP来搞 假如已知g[i][j][k],我们可以枚举下一位和k合并的区间是哪一段,设为[j+1,p],首先要保证该区间mod m-1=1 ,也就是最后消除完只剩下一个,那么就可以进行合并了.注意要特判k合并之后刚好m位的情况.
2017-01-31周二(81)
▲18:06:53 BZOJ2301 problem b(HAOI2011) 莫比乌斯反演/线性筛/分块
莫比乌斯反演的定理:
F(n)=∑f(d) d是n 的因子 -> f(n)=∑μ(d)*F(n/d) d是n的因子
F(n)=∑f(d) d是n 的倍数 -> f(n)=∑μ(d/n)*F(d) d是n的倍数

可以用一发容斥,把问题转化为4个小问题-> x的范围在[1,A],y 的范围[1,B],求(x,y)符合的个数
定义F(i)表示以i的倍数为gcd的数对个数,f(i)表示以i为gcd的数对个数
则满足定理的第二个形式.现在要求f(m),即∑μ(i)*F(i) i是m的倍数
而F(i)是可以直接求出=(A/i)*(B/i).
那么暴力就是直接for m的每个倍数,但在m较小的情况下就狗带了,下面优化:
首先有一个神奇的结论:n/d的值最多有2*sqrt(n)个,那么把F(i)相同的一些i看成一个块一起算,至于∑μ(i)可以利用前缀和得到区间的值.
这样最后的复杂度为O(n*sqrt(n))

#include<cstdio> #include<cstring> #include<algorithm> #include<iostream> #define ll long long using namespace std; const int M=50005;// int mark[M],n,mu[M],sum[M],pri[M],tot=0,a,b,c,d,m;//*ans 要ll */ inline void rd(int &res){ res=0;char c; while(c=getchar(),c<48); do res=(res<<1)+(res<<3)+(c^48); while(c=getchar(),c>=48); } void print(ll x){ if(!x)return ; print(x/10); putchar((x%10)^48); } void sc(ll x){ if(x<0){x=-x;putchar('-');} print(x); if(!x)putchar('0'); putchar('\n'); } void Init(){//线性筛 得到mobius函数 mu[1]=1; int i,j,k; for(i=2;i<M;i++){ if(!mark[i]){//素数 pri[++tot]=i; mu[i]=-1; } for(j=1;j<=tot&&pri[j]*i<M;j++){ mark[pri[j]*i]=1; if(i%pri[j]==0){ mu[i*pri[j]]=0; break; } mu[pri[j]*i]=-mu[i]; } } } ll work(int A,int B){// A/=m;B/=m; if(A>B)swap(A,B);//默认A较小 if(!A)return 0; int en;////从1倍开始 ll ans=0; for(int i=1;i<=A;i=en+1){//表示的是 en=min(A/(A/i),B/(B/i)); ans+=1ll*(sum[en]-sum[i-1])*(A/i)*(B/i); } return ans; } void solve(){ int i,j,k; Init(); for(i=1;i<M;i++)sum[i]=mu[i]+sum[i-1];//得到前缀和 rd(n); while(n--){ rd(a);rd(b);rd(c);rd(d);rd(m); ll ans=work(b,d)-work(a-1,d)-work(b,c-1)+work(a-1,c-1); sc(ans); } } int main(){ // freopen("da.in","r",stdin); solve(); return 0; }
2017-02-01周三(84)
▲07:53:48 BZOJ3529 数表(SDOI2014) 莫比乌斯反演/分块/离线/树状数组
▲10:50:57 BZOJ2154 Crash的数字表格 莫比乌斯反演/分块 n/d的取值个数不超过2*sqrt(n)是非常重要的结论!! 假如要求gcd为k的数对,且k很多的情况,可以将a,b同时除以k,问题就转化成求 a/k,b/k互素的情况.又由于上面的结论,所以把复杂度优化到sqrt(n).剩余的就是莫比乌斯反演的模板了.
▲14:07:27 BZOJ2693 jzptab 【精神AC】是上一题的加强版,多组case 上一题中最后的式子:
∑d*f(d)=∑d*∑μ(i)*i^2*sum(n/di)*sum(m/di)
我们可以把d*i看作一个整体,sum(n/di)*sum(m/di)提前,再处理出 ∑d*μ(i)*i*2的前缀和就可以实现sqrt(n)的复杂度
由于莫比乌斯函数的积性函数,因此它的和也是积性函数,假设 h(D)=∑D/i*μ(i)*i^2
可以在线性筛过程中处理出h数组,假如D是质数,直接得到h(D)=D-D*D
假如D的所有质因数次数<=1 h(D)=h(i)*h(pri[j]) 根据积性
否则 h(D)=h(i)*pri[j] 因为pri[j]所带来的因数都是无贡献的,只是把式子中的D增大了而已
2017-02-02周五(85)
▲10:41:52 BZOJ4652 循环之美(NOI2016) 莫比乌斯反演/杜教筛/推推推猜猜猜
首先要得到一个结论: 所有符合条件的(x,y)必定满足gcd(y,z)=gcd(x,y)=1.至于这个结论是怎么得到的...看造化了..(反正我是模拟出来的)有了这个结论之后就可以乱搞了.
列出式子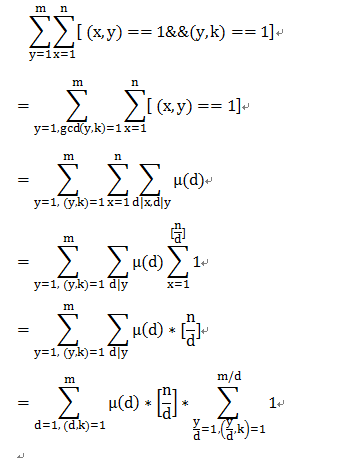
按n/d和m/d可以将d分成O(sqrt(n))块
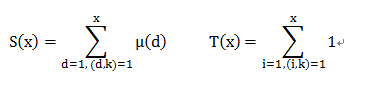
现在问题就是求出S(x),T(x)
我们进行递推
设s(i,x)为小于等于x的,与k的前i种质因子的乘积互质的自然数的μ函数的和
t(i,x)为小于等于x的,与k的前i种质因子的乘积互质的自然数的个数
s(i,x)=s(i−1,x)+s(i,x/pi)
t(i,x)=t(i−1,x)−t(i−1,x/pi)
为了求出s,需要知道μ的前缀和,此时就用到了杜教筛-> sum(n)=1-∑sum(n/i) i∈[2,n]
用map来计划搜索
2017-02-12周日(89)
▲08:07:10 Sum of LCMs/Sum of LCMs II 积性函数求和/推推推
①与n互质且小于n的数的和就是phi(n)*n/2
②∑phi(d)=n (d|n)
首先把答案化成 ∑phi(d)*d*d*(n/d+1)*(n/d)/2的形式 然后问题转化成求f(i)=phi(i)*i*i的前缀和
再通过式子②进行化简.化成sum(i)=B-∑f(j)*g(i/j)的形式然后就可以递推求解.

void init(){ for(int i=1;i<=n;i++)phi[i]=i; for(int i=2;i<=n;i++){ if(phi[i]==i){ for(int j=i;j<=n;j+=i)phi[j]=phi[j]/i*(i-1); } } }
▲09:21:08 HDU1695 GCD 莫比乌斯反演/容斥
▲11:04:10 BZOJ2440 完全平方数 莫比乌斯反演/二分/结论:1到x中不含平方因子的个数为∑mu[i]*(x/(i^2)) i<=sqrt(x) 【可用容斥证明】
▲21:15:23 UOJ34 多项式乘积 FFT模板

1 #include<cstdio>
2 #include<iostream>
3 #include<algorithm>
4 #include<cstring>
5 #include<cmath>
6 using namespace std;
7 const int M=3e5+5;
8 #define db double
9 struct node{
10 double r,i;
11 node operator+(const node &tmp)const{return (node){r+tmp.r,i+tmp.i};}
12 node operator-(const node &tmp)const{return (node){r-tmp.r,i-tmp.i};}
13 node operator*(const node &tmp)const{return (node){r*tmp.r-i*tmp.i,i*tmp.r+tmp.i*r};}
14 }a[M],b[M];
15 int n,m;
16 db pi=acos(-1.00);
17 inline void rd(int &res){
18 res=0;char c;
19 while(c=getchar(),c<48);
20 do res=(res<<1)+(res<<3)+(c^48);
21 while(c=getchar(),c>=48);
22 }
23 void pt(int x){
24 if(!x)return;
25 pt(x/10);
26 putchar((x%10)^48);
27 }
28 void sc(int x){
29 if(!x)putchar('0');
30 else pt(x);
31 //putchar()
32 }
33 void fft(node a[],int n,int p){
34 if(n==1)return;
35 node l[n>>1],r[n>>1];//分成左右两个部分
36 for(int i=0;i<n;i+=2)l[i>>1]=a[i],r[i>>1]=a[i+1];
37 fft(l,n>>1,p);fft(r,n>>1,p);
38 node wn=(node){cos(2*pi/n),p*sin(2*pi/n)},w=(node){1,0},t;
39 for(int i=0,en=(n>>1);i<en;i++,w=w*wn){
40 t=r[i]*w;a[i]=l[i]+t,a[i+en]=l[i]-t;
41 }
42 }
43 void solve(){
44 int i,j,k;
45 rd(n);rd(m);n++,m++;
46 for(i=0;i<n;i++)rd(k),a[i].r=(db)k;
47 for(i=0;i<m;i++)rd(k),b[i].r=(db)k;
48 m+=n;
49 for(n=1;n<=m;n<<=1);
50 fft(a,n,1);fft(b,n,1);
51 for(i=0;i<n;i++)a[i]=a[i]*b[i];
52 fft(a,n,-1);
53 for(i=0;i<m-1;i++){
54 sc((int)(a[i].r/n+0.5)); putchar(" \n"[i==m-2]);
55 }
56 }
57 int main(){
58 //freopen("da.in","r",stdin);
59 solve();
60 return 0;
61 }

1 #include<cstdio>
2 #include<iostream>
3 #include<algorithm>
4 #include<cstring>
5 #include<cmath>
6 using namespace std;
7 const int M=3e5+5;
8 #define db double
9 struct node{
10 double r,i;
11 node operator+(const node &tmp)const{return (node){r+tmp.r,i+tmp.i};}
12 node operator-(const node &tmp)const{return (node){r-tmp.r,i-tmp.i};}
13 node operator*(const node &tmp)const{return (node){r*tmp.r-i*tmp.i,i*tmp.r+tmp.i*r};}
14 }a[M],b[M];
15 int n,m,f=1,R[M];
16 db pi=acos(-1.00);
17 inline void rd(int &res){
18 res=0;char c;
19 while(c=getchar(),c<48);
20 do res=(res<<1)+(res<<3)+(c^48);
21 while(c=getchar(),c>=48);
22 }
23 void pt(int x){
24 if(!x)return;
25 pt(x/10);
26 putchar((x%10)^48);
27 }
28 void sc(int x){
29 if(!x)putchar('0');
30 else pt(x);
31 }
32 void fft(node a[],int n){
33 int i,j,k,len;
34 for(i=0;i<n;i++)if(i<R[i])swap(a[R[i]],a[i]);//保证当前的序列是按照Ri排序的
35 for(i=1;i<n;i<<=1){//枚举长度 的一半 即n/2
36 node wn=(node){cos(pi/i),f*sin(pi/i)};
37 for(len=(i<<1),j=0;j<n;j+=len){//len就是当前的长度,j为起点
38 node w=(node){1,0};
39 for(k=0;k<i;k++,w=w*wn){//k+j表示当前访问的点
40 node t=a[j+k],y=w*a[j+k+i];
41 a[j+k]=t+y,a[j+k+i]=t-y;
42 }
43 }
44 }
45 }
46 int main(){
47 int i,j,k,L=0;//L从0开始
48 rd(n);rd(m);n++,m++;
49 for(i=0;i<n;i++)rd(k),a[i].r=(db)k;
50 for(i=0;i<m;i++)rd(k),b[i].r=(db)k;
51 m+=n;
52 for(n=1;n<m;n<<=1,L++);
53 for(i=0;i<n;i++)R[i]=(R[i>>1]>>1)|((i&1)<<(L-1));//R[i]表示i的二进制翻转过来的数字
54 fft(a,n);
55 fft(b,n);
56 for(i=0;i<n;i++)a[i]=a[i]*b[i];
57 f=-1;
58 fft(a,n);
59 for(i=0;i<m-1;i++){
60 sc((int)(a[i].r/n+0.5));
61 putchar(" \n"[i==m-2]);
62 }
63 return 0;
64 }
2017-02-13周一(92)
▲08:02:27 HDU1402 A*B problem FFT模板 /注意判断前导0
▲14:01:35 HDU4609 3-idiots 求递推式+FFT优化 要考虑全所有不同的情况,比如三个长度/两个长度相同
▲16:45:36 UVA4671 K-neighbor substrings FFT/把判断海明距离写成卷积的形式 F(i)=∑a(j)*b(i-j)把B串反向来构造.这里我用的是把a变为1,b为-1,那么相同的乘积就是1,从而得到相同的对数,注意当多项式系数为负数时值要减去0.5. 当然还有一种做法,就是分别判断两个都是a,和两个都是b的情况,判断a时,把a赋为1,b为0,那么结果就是表示两者都为a的情况数了.最后再用hash判重.
我做到了嘿嘿嘿~~
2017-02-14周二(94)(Happy 狗粮 Day)
▲14:23:20 NOI十连测1 T1 奥义商店 分块/分类决策/概率
30分的暴力和20分的简单分块很好搞!!
那就来讲讲正解吧.30分的暴力我想得太复杂了,我直接考虑等差数列的左右端点再计算和,但是这是非常非常复杂的!
有更简单算期望值的方法:
计算y=k+x*d的每个点y 的出现的概率 那么总的期望就是每个y对应的p(y)*v(y)
这样问题就简单多了!!你是不是sa!!!(后缀数组表示一脸懵逼)
这样暴力就是O(n^2)
假设y与k的距离x个d,设他们的距离为x,p(x)=p(x-1)*(c-x+1/n-x) 我们会发现 当x大到某一个范围时,p(x)几乎为0了..并且x不会很大.
那么只要求出这个x就可以了.
当t=1时,就是20分的做法,分类决策+分块.
[关于概率和期望]尽量把事件独立开计算贡献大小/当概率小到一定程度可以忽略不计
▲14:43:53 NOI十连测1 T2 访问计划 结论/树形DP 结论:一条(fa[x],x)的边被计算的次数的奇偶性等于x子树内被选中连边的点的奇偶性.根据往返的性质是可以感性地证明...知道了这一点之后就可以直接树形DP,f[i][j]表示i子树内有j个节点被选中的边的最小和.背包一下就可以了.
想的时候可以考虑每进行一次操作对答案的影响是什么.
2017-02-15 周三(96)
▲14:21:25 HDU4093/UVA5705 FFT/容斥记数 推公式即可

1 #include<cstdio>
2 #include<algorithm>
3 #include<cmath>
4 #include<cstring>
5 #include<iostream>
6 using namespace std;
7 const int M=131075;
8 int R[M],n,p,m;
9 struct node{
10 long double r,i;
11 void init(){r=i=0;}
12 node operator+(const node &tmp)const{return (node){r+tmp.r,i+tmp.i};}
13 node operator-(const node &tmp)const{return (node){r-tmp.r,i-tmp.i};}
14 node operator*(const node &tmp)const{return (node){r*tmp.r-i*tmp.i,i*tmp.r+r*tmp.i};}
15 }c[M],f[6][M],g[6][M];
16 long double pi=acos(-1.0),eps=1e-9;
17 inline void rd(int &res){
18 res=0;char c;
19 while(c=getchar(),c<48);
20 do res=(res<<1)+(res<<3)+(c^48);
21 while(c=getchar(),c>=48);
22 }
23 void print(int x){
24 if(!x)return ;
25 print(x/10);
26 putchar((x%10)^48);
27 }
28 void sc(int x){
29 if(x<0){x=-x;putchar('-');}
30 print(x);
31 if(!x)putchar('0');
32 // putchar('\n');
33 }
34 void fft(node a[],int m,int fi){
35 int i,j,k,t;
36 for(i=0;i<m;i++)if(i<R[i])swap(a[i],a[R[i]]);
37 for(i=1;i<m;i<<=1){
38 node wn=(node){cos(pi/i),fi*sin(pi/i)};
39 for(t=(i<<1),j=0;j<m;j+=t){
40 node w=(node){1,0};
41 for(k=0;k<i;k++,w=w*wn){
42 node x=a[j+k],y=w*a[j+k+i];
43 a[j+k]=x+y,a[k+j+i]=x-y;
44 }
45 }
46 }
47 }
48 void Add(node a[],int k,node b[]){
49 for(int t=0;t<m;t++)a[t].r+=(k*(long long)(b[t].r/m+0.5));
50 }
51 void solve(int cas){
52 printf("Case #%d:\n",cas);
53 int L=0,i,j,t,k=0,x;
54 rd(n);rd(p);
55 for(i=1;i<=n;i++){
56 rd(x);
57 for(j=1;j<=p;j++)g[j][x*j].r=1.0;
58 k=max(k,x*p);
59 }
60 f[0][0].r=1.000;
61 for(m=1;m<=k;m<<=1)L++;
62 for(i=0;i<m;i++)R[i]=(R[i>>1]>>1)|((i&1)<<L-1);
63 for(i=1;i<=p;i++)fft(g[i],m,1);
64 for(i=1;i<=p;i++){
65 fft(f[i-1],m,1);
66 for(j=k=1;j<=i;j++,k*=-1){
67 for(t=0;t<m;t++)c[t]=g[j][t]*f[i-j][t];
68 fft(c,m,-1);
69 Add(f[i],k,c);
70 }
71 for(t=0;t<m;t++)f[i][t].r/=i;
72 }
73 for(i=0;i<m;i++){
74 if(f[p][i].r>1-eps){
75 sc(i);putchar(':');putchar(' ');
76 printf("%.0Lf\n",f[p][i].r);
77 }
78 }
79 puts("");
80 for(j=0;j<m;j++){
81 for(i=0;i<=p;i++)
82 g[i][j].init(),f[i][j].init();
83 c[j].init();
84 }
85 }
86 int main(){
87 freopen("da.in","r",stdin);
88 freopen("my.out","w",stdout);
89 int cas;
90 rd(cas);
91 for(int i=1;i<=cas;i++)solve(i);
92 return 0;
93 }
▲22:28:52 NOI十连测2 T1 深邃 二分+贪心搞一发 看到【最大值最小】就要二分啊!补药犹豫啊!!那么检验就比求最值简单得多.然后可以根据决策和终态枚举来考虑贪心的方向~
2017-02-16周四(97)
NTT:就是把FFT中的小数运算由模数的性质转化成整数运算的工具.这里的模数需要具备一些性质->可以写成k*2^p+1的形式!比如1004535809,998244353等等.....
FFT在多项式系数很大时会丢失精度!慎用!!(调都调不出来哟!!当心哟!!)
▲22:08:41 BZOJ3456 城市规划 求一个n个点的联通块的方案数(点有标号) ->这个问题就是解决[黑暗]的第一步.
设f(n)为n个点的联通块的方案数,h(n)为n个点的简单图的方案数,有h(n)=2^C(n,2),f(n)=h(n)-∑f(k)*h(h-k)*C(n-1,k-1) k∈[1,n-1] .
那么可以用分治FFT/NTT或者多项式求逆来解决.这里贴一下分治的做法.
(在分治区间<=S时暴力求卷积是一个小优化哟!!~)

#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#define ll long long
using namespace std;
const int M=(1<<18)+5;
const int ri=3;
const int P=1004535809;
int pw[M][2];//1是逆元
int m,n,h[M],f[M],w[M],a[M],b[M],c[M],inv[M],R[M],fac[M];
inline void rd(int &res){
res=0;char c;
while(c=getchar(),c<48);
do res=(res<<1)+(res<<3)+(c^48);
while(c=getchar(),c>=48);
}
int Pw(int x,ll y){
int res=1;
while(y){
if(y&1)res=1ll*res*x%P;
x=1ll*x*x%P;
y>>=1;
}
return res;
}
void Add(int &x,int y){
x+=y;if(x>=P)x-=P;
else if(x<0)x+=P;
}
void ntt(int a[],int n,bool fi){
int i,j,k,len;
for(i=0;i<n;i++)if(i<R[i])swap(a[i],a[R[i]]);
for(i=1;i<n;i<<=1){
len=i<<1;
int w,g=pw[len][fi];
for(j=0;j<n;j+=len){
for(k=0,w=1;k<i;k++,w=1ll*w*g%P){
int x=a[k+j],y=1ll*w*a[k+j+i]%P;
Add(a[k+j]=x,y);
Add(a[k+j+i]=x,-y);
}
}
}
}
int S=20;
void work(int l,int r){
if(l==r)return;
int i,j,k,L=0,mid=l+r>>1,t=mid-l+1,len=r-l+1;
// printf("t= %d\n",t);
if(len<=S){
for(i=l+1;i<=r;i++){
for(j=l;j<i;j++){
Add(f[i],-1ll*f[j]*inv[j-1]%P*h[i-j]%P*fac[i-1]%P);
}
}
return ;
}
work(l,mid);
for(n=1;n<=len;n<<=1,L++);
int inv_n=Pw(n,P-2);
for(i=0;i<n;i++)R[i]=(R[i>>1]>>1)|((i&1)<<L-1);
for(i=1;i<=t;i++)a[i]=1ll*f[i+l-1]*inv[i+l-2]%P;
for(i=1;i<len;i++)b[i]=h[i];
for(i=t+1;i<n;i++)a[i]=0;
for(i=len;i<n;i++)b[i]=0;
a[0]=b[0]=0;
ntt(a,n,0);ntt(b,n,0);
for(i=0;i<n;i++)c[i]=1ll*a[i]*b[i]%P;
ntt(c,n,1);
for(i=t+1;i<=len;i++)Add(f[i+l-1],-1ll*c[i]*inv_n%P*fac[i+l-2]%P);
work(mid+1,r);
//先求出[l,mid]的值,然后再去更新[mid+1,r] 用ntt去更新
//f记录的是好的值
}//a,b来记录两个
void solve(){
int i,j,k=m<<1;
fac[0]=inv[0]=1;
for(i=1;i<=m;i++){
f[i]=h[i]=Pw(2,1ll*i*(i-1)/2);
fac[i]=1ll*fac[i-1]*i%P;
inv[i]=Pw(fac[i],P-2);
h[i]=1ll*h[i]*inv[i]%P;
}
for(i=1;i<k;i<<=1){
pw[i][0]=Pw(ri,(P-1)/i);
pw[i][1]=Pw(pw[i][0],P-2);
}
f[1]=1;//一个点的方案数为1
work(1,m);//处理[l,r]之间的数
printf("%d\n",f[m]);
}
int main(){
freopen("da.in","r",stdin);
rd(m);
solve();
return 0;
}
2017-02-17周五(99)
▲10:41:24 NOI2016十连测2 T2 黑暗 分治FFT/NTT/斯特林数/数学式子推推推
考试时推出了一个式子A,但是需要求出[城市规划]中的f(n),没有推出这个式子所以狗带了...那么假设现在已求出f(n),就可以通过A
F(a,b)=g(k)*F(a-k,b-1)*C(a-1,k-1)来求出F(a,b).总复杂度O(n^2logn)60分get了~以上的思路都是很正常的.正解就是非人哉了.
切入点在于m,m很小,只有15,我们可以把n^m次方 写成其(奇)他(怪)的形式.
n^m=∑{m,k}*C(n,k)*k! (0<=k<=m) {a,b}是第二类斯特林数,表示a个不同元素拆分成b个集合的方案数.
m很小所有可以暴力预处理出第二类斯特林数,公式如下:
{m+1,k}=k*{m,k}+{m,k-1}
那接下来就是C(n,k)*k!的部分了 ,它0表示的是联通块的个数为n的图对答案的贡献.
C(n,k)*k!可以看做是一个图联通块个数为n,在其中有序地选k个的方案数,那么我们考虑怎么求.
其实不一定要确切知道联通块个数分别为k的结果,只要求出每个图的总和就可以了.
那么就设H(i,j)表示i个点的图,在图的联通块个数中有序的选j个的方案数.
H(i,j)=∑g(k)*C(n,k)*H(i-k,j-1)这个可以用ntt来搞.
H(i,1)=∑g(k)*C(i,k)*h(i-k)...求出H之后,ans(n,m)=∑{m,k}*H(n,k) (1<=k<=m)
然后这道题就做完了..真是奥妙重重~
最重要的是把n^m转化和C(n,k)*k转化的两步.
▲16:13:01 ZOJ 3856 FFT计数 分类讨论+特殊情况+FFT模板
▲CF 765E Tree Folding对于操作有点小奇怪的题目可以 正难则反!!把操作过程倒过来!!一下子豁然开朗啊!!
▲CF 765F Souvenir 线段树/离线/YY 把所有询问按照右端点排序,线段树节点[l,r]记录当前询问区间的左端点在[l,r]范围中的最小差.
根据询问逐个更新r,每次更新一个r就考虑它对一个节点[L,R]的影响.
那就需要在线段树节点上存[l,r]对应的序列,要用到指针.
这个思路好像是第一次见到!!神奇~~
2017-02-18周六(100)
▲10:12:44 [100题纪念] NOI2016十连测2 T3 后缀自动机+二分搞一发哈哈哈哈我太棒了!!!!
2017-02-19周日(103)
▲14:33:01 codechef Arithmetic Progressions FFT+分块 ①分类讨论情况要考虑全 ②块的大小要算清楚!!③开Long long啊啊啊啊!!!!
▲21:19:23 NOI2016十连测3 T2 分块/倍增+线段树 根据终态,执行完[l,r]的操作,k一定会被某个包含k的区间更新到,如果能求出这个区间,就可以解决问题了.暴力做法就是枚举[l,r]从后往前,依次更新当前最远的l和r.优化我选择了分块,预处理出每一个点在每一块操作结束之后扩展的左右区间.然后查询时复杂度为O(sqrt(n)).正解的做法是倍增..其实意思是一致的..
倍增做法:
1)处理出每个操作p向前伸展2^j次的操作是什么,设为fl[p][j],fr[p][j].我们按照顺序进行每一个操作,进行p操作之间找到当前覆盖l[p]和r[p]的操作,就是fl[p][0],fr[p][0]的值.
2)处理出每个询问p,在<=R范围中,最晚的包含k的操作,可以通过离线按照询问的r排序,和操作一起,边更新边处理结果.那么处理询问p时,只更新了<=R的操作,那就可以得到最晚的包含k的操作了.
用(q+m)(logn+logm)就可以得到以上两个信息.处理答案时,只要倍增一下,求出边界l,r,再求区间最值就可以了/.
▲21:37:51 NOI2016十连测3 T1 概率 我又把问题想复杂了(哭./_\.)...①很明显每个数字每轮出现的概率是一样的 ②考虑每一轮某个数字出现的概率,假设还剩下y个数字,所有选择的方式有(y-1)*y/2种,y个数字里肯定有一个数字包含x,那么一共有y-1种选法,那么概率就是2/y,然后得到每一轮的概率和就可以了.
2017-02-20周一(103)
▲19:55:53 NOI2016十连测3 T3 今天一整天都在刚这一道题啊啊啊啊!!!我的做法:有一个猜想:每个状态a的下一个状态一定是由交换a序列的相邻两个得到的.那么每次得到一个状态就直接枚举相邻两个可交换的就可以了.考试的代码得了40分.接下来可以优化到85分.
1.记录每个状态的a序列在出队列时再求出.因为每个状态肯定是由上一个状态交换相邻两点得到,所以只要记录上一个的id和交换的位置就可以了,等到出队列时具体记下来.因为有很多状态是不会出队列的,最终出队列的状态只有m个,所以这样可以优化空间.
2.用一个大顶堆,维护前m大的值,如果当前状态比m个中最大的还要大,肯定不会算入答案里,这样可以减少进入堆里的 状态数.
3.在扩展的过程中,可能会出现重复的状态,所以我进行了哈希判重.求哈希值可以直接通过上一个状态的哈希值O(1)求出.注意这里判重用到了两个素数.减少冲突.
2017-02-21周二(106)
▲13:39:32 QTREE1 修改某条边权,求路径边权最大值 树链剖分/LCT裸题

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
using namespace std;
const int M=1e4+5;
int ec=1,tot=0,n;
int seq[M],id[M],num[M],sz[M],son[M],top[M],w[M];
int head[M],nxt[M<<1],to[M<<1],ed[M<<1],v[M],fa[M],dep[M];
inline void Max(int &x,int y){if(x<y)x=y;}
inline void rd(int &res){
res=0;char c;
while(c=getchar(),c<48);
do res=(res<<1)+(res<<3)+(c^48);
while(c=getchar(),c>=48);
}
void print(int x){
if(!x)return ;
print(x/10);
putchar((x%10)^48);
}
void sc(int x){
print(x);
if(!x)putchar('0');
putchar('\n');
}
struct Seg{
int mx[M<<2];
void build(int L,int R,int p){
if(L==R){mx[p]=v[num[seq[L]]];return;}
int mid=L+R>>1;
build(L,mid,p<<1);
build(mid+1,R,p<<1|1);
mx[p]=max(mx[p<<1],mx[p<<1|1]);
}
void upd(int L,int R,int a,int x,int p){
if(L==R){mx[p]=x;return;}
int mid=L+R>>1;
if(a<=mid)upd(L,mid,a,x,p<<1);
else upd(mid+1,R,a,x,p<<1|1);
mx[p]=max(mx[p<<1],mx[p<<1|1]);
}
int qry(int L,int R,int l,int r,int p){
if(L==l&&R==r)return mx[p];
int mid=L+R>>1;
if(r<=mid)return qry(L,mid,l,r,p<<1);
else if(l>mid)return qry(mid+1,R,l,r,p<<1|1);
else return max(qry(L,mid,l,mid,p<<1),qry(mid+1,R,mid+1,r,p<<1|1));
}
}T;
int Qry(int a,int b){
int res=0,t1=top[a],t2=top[b];
while(t1!=t2){
if(dep[t1]<dep[t2]){swap(t1,t2),swap(a,b);}
// printf("%d %d %d %d\n",t1,a,t2,b);
// if(w[t1]+1<=w[a])
Max(res,T.qry(1,n,w[t1],w[a],1));
a=fa[t1];t1=top[a];
}
if(a!=b){
if(dep[a]<dep[b])swap(a,b);//a的深度更大
Max(res,T.qry(1,n,w[b]+1,w[a],1));
}
return res;
}
void dfs(int x,int par){
fa[x]=par;
sz[x]=1;
dep[x]=dep[par]+1;
for(int i=head[x];i;i=nxt[i]){
int y=to[i];
if(y==par)continue;
id[ed[i]]=y;
num[y]=ed[i];
dfs(y,x);
if(sz[y]>sz[son[x]])son[x]=y;
sz[x]+=sz[y];
}
}
void build(int x,int tp){
w[x]=++tot;
seq[tot]=x;
top[x]=tp;
if(son[x])build(son[x],tp);
for(int i=head[x];i;i=nxt[i]){
if(to[i]!=fa[x]&&to[i]!=son[x])build(to[i],to[i]);
}
}
void clear(){
ec=1;tot=0;
for(int i=1;i<=n;i++)head[i]=son[i]=sz[i]=top[i]=dep[i]=0;
}
void ins(int a,int b,int c){
to[ec]=b;nxt[ec]=head[a];ed[ec]=c;head[a]=ec++;
to[ec]=a;nxt[ec]=head[b];ed[ec]=c;head[b]=ec++;
}
void solve(){
int i,j,c,a,b;
char s[10];
rd(n);
for(i=1;i<n;i++){
rd(a);rd(b);rd(v[i]);
ins(a,b,i);
}
dfs(1,0);
build(1,1);
T.build(1,n,1);
while(scanf("%s",s)&&s[0]!='D'){
rd(a);rd(b);
if(s[0]=='Q')sc(Qry(a,b));
else {
v[a]=b;
T.upd(1,n,w[id[a]],b,1);
}
}
clear();
}
int main(){
int cas;
rd(cas);
while(cas--)solve();
return 0;
}
▲14:11:03 QTREE2 求路径长度/求路径上第K个点/无修改 倍增LCA
▲14:41:47 QTREE3 翻转一个点的颜色/求一个点到根的深度最小的黑点 BIT+倍增(二分)
2017-02-22 周三 ヾ(o◕∀◕)ノヾ(109)
▲10:00:03 NOI2016十连测R4 T1 二进制的运算 YY!!神题!!
异或: 因为a^b=c,当a和c固定之后,b的值是唯一确定的,所以可以从高位往下贪心即可.复杂度为O(nlogm).
因为数字的范围为2^16,很大,可以考虑把数字分成两部分,前8位和后8位,如果只考虑前8位的情况,枚举前8位的数字是x,就可以得到ai和x操作后的结果,但是我们不知道后8位的结果,因为后8位最多只有2^8种可能,所以对于每个ai,可以枚举后八位的数字为j,预处理出ai的后八位和0~2^8之间的每个数操作后的结果.这样询问和更新的复杂度都是O(n*sqrt(m))
奥妙重重!!!太神了!!!
▲14:58:41 NOI2016十连测R4 T2 可持久化字符串 题目已经给足了暗示啊有没有!!!比赛的时候我用了KMP+倍增哈哈哈想KMP中得pre数组可以直接求出最小循环节长度,并且复杂度不是线性的吗~那么此题就可以解啦!然后心里默默嘲笑此题太简单,简直是NOIP难度啊!!敲完之后自己造了一个30万的数据,但是太水了...所以很快跑出来,一点都没有意识到自己错了..现在看来自己真的是 Too young Too simple!! (/▽╲)
一个串S(长度为n)的最小循环节长度 为 n-pre[n]
其实我大致的思路是没错的,倍增也是对的,但就在一点上除了问题:KMP的复杂度均摊是O(n)的,但是因为题中给出的串会破坏均摊的结构,比如22222222222222234567,这个串,在34567每个数字求pre都要扫一遍每个2,所以就狠狠地T掉了..
所以现在的问题就在于如何快速地求出pre.我们可以模拟正常KMP的过程,就是判断当前的j后面的字符和当前要比较的字符是否相同,若不同,根据j=pre[j]迭代下去.
假如我们对于每个j都记录对于每个字符x,从j开始迭代得到的pre值.如果暴力存储,空间肯定狗带了..
可以发现,对于j和pre[j]这两个点对于每个字符的答案,除了pre[j]后面的字符,其他都是一样的,所以我们可以通过可持久化线段树进行修改,将j的答案全部设为prej的答案,然后在对pre[j]的后一个字符对应的值进行修改即可.
这里找到j的后一个字符用的是倍增法.
时间空间的复杂度都是O(nlogm).

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
using namespace std;
const int M=3e5+5;
const int S=20;
inline void rd(int &res){
res=0;char c;
while(c=getchar(),c<48);
do res=(res<<1)+(res<<3)+(c^48);
while(c=getchar(),c>=48);
}
void print(int x){
if(!x)return ;
print(x/10);
putchar((x%10)^48);
}
void sc(int x){
if(x<0){x=-x;putchar('-');}
print(x);
if(!x)putchar('0');
putchar('\n');
}
int n,m,typ,d[M],c[M],fa[M][S],pre[M],rt[M],ls[M*30],rs[M*30],val[M*30],tot=0,mp[1<<S];
int p,v;
int Up(int x,int d){
while(d){
int k=d&-d;
x=fa[x][mp[k]];
d-=k;
}
return x;
}
int qry(int x,int L,int R){
if(L==R)return val[x];
int mid=L+R>>1;
if(p<=mid)return qry(ls[x],L,mid);
else return qry(rs[x],mid+1,R);
}
void upd(int &id,int pre,int L,int R){
id=++tot;
ls[id]=ls[pre];rs[id]=rs[pre];
if(L==R){
val[id]=v;return;
}
int mid=L+R>>1;
if(p<=mid)upd(ls[id],ls[pre],L,mid);
else upd(rs[id],rs[pre],mid+1,R);
}
void solve(){
int i,j,k,ans=0;
rd(n);rd(m);rd(typ);
for(i=0;i<S;i++)mp[1<<i]=i;
for(i=1;i<=n;i++){
rd(fa[i][0]);rd(c[i]);
if(typ)fa[i][0]^=ans,c[i]^=ans;
d[i]=d[fa[i][0]]+1;
for(j=1;j<S&&(1<<j)<=d[i];j++)fa[i][j]=fa[fa[i][j-1]][j-1];
p=c[i],pre[i]=qry(rt[fa[i][0]],1,m);
ans=d[i]-d[pre[i]];
sc(ans);
k=Up(i,ans-1);//找到pre[i]下面一个东西
p=c[k];v=k;
upd(rt[i],rt[pre[i]],1,m);//自己的这个树上就比prei多一个东西
}
}
int main(){
solve();
return 0;
}
▲22:18:57 NOI2016十连测R4 T3 反函数 点分治/FFT 这道题好大啊!!
暴力就直接以每个点作为树根,往下遍历,同时得到答案.比赛时就因为一个细节没写好,+30分就滚粗了.
注意括号序列必须是合法的,所以要及时判断不合法的情况!!!
正解:
点分治,每次处理以rt为根的子树中以rt为LCA的所有路径答案.
我们把"("记为1, ")"记为-1,从rt往下遍历,处理出每个点的前缀和为sum,若sum[x]为x到rt的最小值,并且是第k个最小值,那么tmn[x]=k,tmx[x]同理.假如(x->rt->y)是一个合法的序列,一定满足:sum[x],sum[y]分别是各自到rt的路径上的点的sum的最大值/最小值,并且sum[x]+sum[y]-f[rt]=0.
且这段路径可以分成的段数,为tmn[x]+tmx[x]-1.
那么预处理出sum和tmn这几个数组之后,把所有点按照sum分类,确定了sum[x]之后就可以确定sum[y].那么答案统计ans[i-1]=∑A[j]*B[i-j] A[j]表示sum为t,并且tmx为j的个数,B[j]表示sum为f[rt]-t,并且tmn为j的个数.这是一个卷积的形式,只要NTT就可以快速求解.
注意这里的x,y有可能在rt的同一个儿子之内,所以要再对rt的每个儿子求一遍答案,它的最终答案的贡献是负的.

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
const int M=65536;
const int P=479*(1<<21)+1;
const int ri=3;
const int oo=1e9+5;
struct G{
int head[M<<1],e,to[M],nxt[M];
void ins(int a,int b){
a+=M;to[e]=b;nxt[e]=head[a];head[a]=e++;
}
}G;
int sum[M],tmx[M],tmn[M],head[M],nxt[M<<1],to[M<<1];
int ec=1,clo=0,soncnt=0,dl[M],dr[M],seq[M],son[M];
int A[M],B[M],C[M];
int mxsum,mnsum,R[M],f[M],n,m,vis[M],sz[M],mxsz[M],rt,res[M],g[M][2];
inline void rd(int &res){
res=0;char c;
while(c=getchar(),c<48);
do res=(res<<1)+(res<<3)+(c^48);
while(c=getchar(),c>=48);
}
void print(int x){
if(!x)return ;
print(x/10);
putchar((x%10)^48);
}
void sc(int x){
if(x<0){x=-x;putchar('-');}
print(x);
if(!x)putchar('0');
putchar('\n');
}
inline void Max(int &x,int y){if(x<y)x=y;}
inline void Min(int &x,int y){if(x>y)x=y;}
void Add(int &x,int y){
x+=y;
if(x>=P)x-=P;
else if(x<0)x+=P;
}
int Pw(int a,int b){
int res=1;
while(b){
if(b&1)res=1ll*res*a%P;
a=1ll*a*a%P;
b>>=1;
}
return res;
}
void ins(int a,int b){
to[ec]=b;nxt[ec]=head[a];head[a]=ec++;
to[ec]=a;nxt[ec]=head[b];head[b]=ec++;
}
void dfs(int x,int par){
sz[x]=1;mxsz[x]=0;
for(int i=head[x];i;i=nxt[i]){
int y=to[i];
if(y==par||vis[y])continue;
dfs(y,x);
sz[x]+=sz[y];
Max(mxsz[x],sz[y]);
}
}
void find_center(int st,int x,int par){
Max(mxsz[x],sz[st]-sz[x]);
if(rt==-1||mxsz[x]<mxsz[rt])rt=x;
for(int i=head[x];i;i=nxt[i]){
if(!vis[to[i]]&&to[i]!=par)find_center(st,to[i],x);
}
}
void rdfs(int x,int par,int mn,int t1,int mx,int t2){
dl[x]=++clo;
seq[clo]=x;
sum[x]=sum[par]+f[x];
tmx[x]=tmn[x]=0;
if(sum[x]>mx)mx=sum[x],tmx[x]=t2=1;
else if(sum[x]==mx)tmx[x]=++t2;
if(sum[x]-f[rt]<mn)mn=sum[x]-f[rt],tmn[x]=t1=1;
else if(sum[x]-f[rt]==mn)tmn[x]=++t1;
Max(m,max(t2,t1));
for(int i=head[x];i;i=nxt[i]){
if(to[i]==par||vis[to[i]])continue;
if(x==rt)son[++soncnt]=to[i];
rdfs(to[i],x,mn,t1,mx,t2);
}
dr[x]=clo;
}
void ntt(int a[],int n,int fi){
int i,j,k,t;
for(i=0;i<n;i++)if(i<R[i])swap(a[i],a[R[i]]);
for(i=1;i<n;i<<=1){
t=i<<1;
int w,wn=g[t][fi];
for(j=0;j<n;j+=t){
for(k=0,w=1;k<i;k++,w=1ll*w*wn%P){
int x=a[k+j],y=1ll*w*a[k+i+j]%P;
Add(a[k+j]=x,y);
Add(a[k+j+i]=x,-y);
}
}
}
}
void calc(int p,int x){
int y,i,j,k,t=0,L=0,a,b,c;
mxsum=-oo;
for(i=dl[x];i<=dr[x];i++){
y=seq[i];
if(y!=rt)G.ins(sum[y],y);
Max(mxsum,sum[y]);
}
if(x==rt){//特殊情况 特判
for(i=G.head[M];i;i=G.nxt[i]){//
y=G.to[i];
if(f[rt]<0)res[tmx[y]]++;
else res[tmn[y]]++;
}
}
for(k=0;k<=mxsum;k++){
a=b=L=0;
c=f[rt]-k+M;
if(c>k+M)continue;
for(j=G.head[k+M];j;j=G.nxt[j]){
y=G.to[j];
if(tmx[y])A[tmx[y]]++;
Max(a,tmx[y]);
}
for(j=G.head[c];j;j=G.nxt[j]){
y=G.to[j];
if(tmn[y])B[tmn[y]]++;
Max(b,tmn[y]);
}
if(!a||!b){
for(i=0;i<=a;i++)A[i]=0;
for(i=0;i<=b;i++)B[i]=0;
continue;
}
for(t=1;t<=a+b;t<<=1)L++;
for(i=0;i<t;i++)R[i]=(R[i>>1]>>1)|((i&1)<<L-1);
ntt(A,t,0);ntt(B,t,0);
for(i=0;i<t;i++)C[i]=1ll*A[i]*B[i]%P;
ntt(C,t,1);
int inv=Pw(t,P-2);
A[0]=B[0]=0;
for(i=1;i<t;i++){
res[i-1]+=1ll*C[i]*inv%P*p;
A[i]=B[i]=0;
}
}
for(i=dl[x];i<=dr[x];i++)G.head[sum[seq[i]]+M]=0;
G.e=1;
}
void conquer(){
sum[rt]=0;
rdfs(rt,rt,oo,0,-oo,0);//得到sum,tmx, tmn
calc(1,rt);
for(int i=1;i<=soncnt;i++)calc(-1,son[i]);
}
void divide(int x){//解决以x为根的子树 把它分开
dfs(x,x);//找到重心(最大子树最小)为rt
rt=-1;clo=soncnt=0;
find_center(x,x,x);
vis[rt]=1;
conquer();
for(int i=head[rt];i;i=nxt[i]){
if(!vis[to[i]])divide(to[i]);
}
}
int main(){
freopen("inverse.in","r",stdin);
freopen("inverse.out","w",stdout);
int i,j,k,a,b;
char s[10];
G.e=1;
rd(n);
for(i=1;i<n;i++){
rd(a);rd(b);ins(a,b);
}
for(i=1;i<=n;i<<=1){
g[i][0]=Pw(ri,(P-1)/i);
g[i][1]=Pw(g[i][0],P-2);
}
for(i=1;i<=n;i++){
scanf("%s",s);
if(s[0]=='(')f[i]=1;
else f[i]=-1;
}
divide(1);
rd(m);
while(m--){
rd(k);sc(res[k]);
}
return 0;
}
2017-02-23 周四(110)
▲11:03:59 QTREE 6 翻转一个点的颜色/问一个点与他相连的同色联通块的大小 BIT大法好!!!
我们把黑点和白点分开考虑.设f[col][i]表示 i节点如果为col色它子树内同色的节点个数.那么对于x节点,它的答案就是x的最浅同色祖先anc(x到anc这一段的颜色相同),答案就是 f[v[x]][anc].
那么考虑如何维护这个数组.
当我们进行翻转一个点x的颜色,只会对x到根路径上的一些连续的点产生影响,只要分类讨论一下即可.然后更新一段路径(a,b) 且a是b的祖先,我们可以通过BIT刷漆和dfs序来搞.单点更新,区间查询.
如何找到anc?? 倍增+BIT.就类似于QTREE3的方法.同时也要维护点到根的权值和即可.

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
using namespace std;
const int M=1e5+5;
const int S=18;
int n,m,dep[M],head[M],to[M<<1],nxt[M<<1],fa[M][S],L[M],R[M],clo=0,ec=1,v[M];//black =0,white =1
inline void rd(int &res){
res=0;char c;
while(c=getchar(),c<48);
do res=(res<<1)+(res<<3)+(c^48);
while(c=getchar(),c>=48);
}
void print(int x){
if(!x)return ;
print(x/10);
putchar((x%10)^48);
}
void sc(int x){
if(x<0){x=-x;putchar('-');}
print(x);
if(!x)putchar('0');
putchar('\n');
}
struct BIT{
int C[M],c;
void add(int a,int b){
while(a<=n){
C[a]+=b;
a+=a&-a;
}
}
int sum(int a){
int res=0;
while(a){
res+=C[a];
a-=a&-a;
}
return res;
}
int qry(int a){
return sum(R[a])-sum(L[a]-1)+c;
}
void modify(int a,int b,int c){
add(L[b],c);
if(fa[a][0])add(L[fa[a][0]],-c);
}
}B[2],g;
void ins(int a,int b){
to[ec]=b;nxt[ec]=head[a];head[a]=ec++;
to[ec]=a;nxt[ec]=head[b];head[b]=ec++;
}
void dfs(int x,int par){
fa[x][0]=par;
dep[x]=dep[par]+1;
L[x]=++clo;
for(int i=head[x];i;i=nxt[i]){
if(to[i]!=par)dfs(to[i],x);
}
R[x]=clo;
}
int find_anc(int x){
int i,a,b=g.sum(L[x]),y=x,c=v[x]*dep[x]+v[x]-b;
for(i=S-1;i>=0;i--){
if(!fa[y][i])continue;
a=g.sum(L[fa[fa[y][i]][0]]);
if(c==v[x]*dep[fa[y][i]]-a)y=fa[y][i];
}
return y;
}
void solve(){
int i,j,k,a,b;
rd(n);
for(i=1;i<n;i++){
rd(a);rd(b);
ins(a,b);
}
dfs(1,0);
for(j=1;j<S;j++){
for(i=1;i<=n;i++)fa[i][j]=fa[fa[i][j-1]][j-1];
}//初始值
for(i=1;i<=n;i++)B[0].add(i,1);
B[0].c=g.c=0;
B[1].c=1;
rd(m);
while(m--){
rd(a);rd(b);
if(a){//翻转颜色 //自己的值是不用改的
if(b==1){
k=(v[b]^1)-v[b];
g.add(L[b],k);g.add(R[b]+1,-k);
v[b]^=1;
continue;
}
int anc=find_anc(fa[b][0]),c=B[v[b]].qry(b),d=B[v[b]^1].qry(b);//在 fa[anc][0]~anc这一段 减掉
if(v[fa[b][0]]==v[b]){
B[v[b]].modify(fa[anc][0],fa[b][0],-c);
B[v[b]^1].modify(fa[b][0],fa[b][0],d);//加上 //后面一个的dep更大
}
else{
B[v[b]].modify(fa[b][0],fa[b][0],-c);
B[v[b]^1].modify(fa[anc][0],fa[b][0],d);
}
k=(v[b]^1)-v[b];
g.add(L[b],k);g.add(R[b]+1,-k);
v[b]^=1;
}
else{
int anc=find_anc(b);//找到 b的同色祖先
sc(B[v[b]].qry(anc));//询问anc的值
}
}
}
int main(){
// freopen("da.in","r",stdin);
// freopen("my.out","w",stdout);
solve();
return 0;
}
2017-02-24 周五 [听说看到初雪会带来好运气哟~](112)
▲11:21:36 UOJ107 APIO2013 T1 机器人 比赛时想了一个很有bug的DP,结果毫无意外地滚粗了.
正确的做法其实差不多.首先预处理出每个点往上下左右四个方向能到达的点.这里只考虑可能停留的点,这样可以减少很多不必要的运算.设f[l][r][k]表示[l,r]的机器人停在k这个点上的最小步数.考虑转移:
f[l][r][k]=min{Min{f[l][mid][k]+f[mid+1][r][k]},Min{f[l][r][h]+1}其中h能一步到达k}
因为所有的点之间没有一定的拓扑关系,所以直接DP是不可行的(这就是比赛代码的错误处)
那么可以用最短路求解.把(l,r,k)当做一个点再根据转移关系连边,跑一边最短路即可.这样60分就能得到了.
正解:可以观察到,转移的部分每次只往前走一步,那能否考虑BFS?因为每个状态可以通过之前的f[l][mid][k]+f[mid+1][r][k]转移,和当前的[l,r]之间的bfs无关,所以可以先处理出f[l][r][k]根据之前的层得到的结果,然后将这些结果从小到大放入队列,保证BFS得到的结果是按照大小顺序的.这里就用到了计数排序.随着队列里的元素的值一起放入队列.

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
inline void rd(int &res){
res=0;char c;
while(c=getchar(),c<48);
do res=(res<<1)+(res<<3)+(c^48);
while(c=getchar(),c>=48);
}
inline void Max(int &x,int y){if(x<y)x=y;}
inline void Min(int &x,int y){if(x==-1||x>y)x=y;}
const int M=505;
const int oo=1e9;
int rx[]={0,1,0,-1},ry[]={1,0,-1,0};
int dir[2][4]={{3,0,1,2},{1,2,3,0}};//A-0-逆-左
int to[M*M][4],id[M][M],tot=0,n,m,t,num[10],seq[M*M],cnt[5000005],in[M*M],A[M*M],q[M*M],f[10][10][M*M];
char mp[M][M];
struct node{
int x,y;
}Q[M*M];
//f值一定>0 如果<=0 说明不存在该种情况
int chk(int a,int b){
if(a<=0||a>n||b<=0||b>m||mp[a][b]=='x')return 1;
if(mp[a][b]=='A'||mp[a][b]=='C')return 2;
return 0;
}
void BFS(int a,int b){
if(!id[a][b])id[a][b]=++tot;
else return;
int L=0,R=0,x,y,i,j,k;//编号
node now=(node){a,b};
Q[R++]=now;
while(L<R){
now=Q[L++];
x=now.x,y=now.y;
for(i=0;i<4;i++){
int tx=x+rx[i],ty=y+ry[i],d=i;
while(1){
while((k=chk(tx,ty))==0){
if(tx==x&&ty==y&&i==d){k=3;break;}tx+=rx[d],ty+=ry[d];
}
if(k==2){//有转向器
d=dir[mp[tx][ty]=='C'][d];
if(tx==x&&ty==y&&d==i){k=3;break;}
tx+=rx[d],ty+=ry[d];
}
else {
tx-=rx[d],ty-=ry[d];
if(k!=3&&(tx!=x||ty!=y)){
if(!id[tx][ty]){
id[tx][ty]=++tot;
node nxt=(node){tx,ty};
Q[R++]=nxt;
}
to[id[x][y]][i]=id[tx][ty];
}
break;
}
}
}
}
}
void work(int l,int r){
int i,j,k,L=0,R=0,u=0,mx=-oo,mn=oo,v,d;
if(l==r){
q[R++]=num[l];
f[l][r][num[l]]=0;
while(L<R){
k=q[L++];
for(i=0;i<4;i++){
if(to[k][i]&&!in[to[k][i]]){
Min(f[l][r][to[k][i]],f[l][r][k]+1);
in[to[k][i]]=1;
q[R++]=to[k][i];
}
}
}
for(i=0;i<R;i++)in[q[i]]=0;
return;
}
for(k=1;k<=tot;k++){//算出初值 然后 直接按照初值从小到大bfs 即可
for(i=l;i<r;i++){
if(~f[l][i][k]&&~f[i+1][r][k])Min(f[l][r][k],f[l][i][k]+f[i+1][r][k]);
}
if(~f[l][r][k]){
seq[++u]=k;
Max(mx,f[l][r][k]);
Min(mn,f[l][r][k]);
}
}
if(mn==oo)return;
for(i=1;i<=u;i++)cnt[f[l][r][seq[i]]]++;
for(i=mn+1;i<=mx;i++)cnt[i]+=cnt[i-1];
for(i=1;i<=u;i++){
int p=cnt[f[l][r][seq[i]]]--;
A[p]=seq[i];
}
for(i=mn;i<=mx;i++)cnt[i]=0;
j=mn,i=1;
while(i<=u&&f[l][r][A[i]]==j){
q[R++]=A[i];
in[A[i]]=1;
i++;
}
while(L<R){
k=q[L++];
v=f[l][r][k]+1;
while(i<=u&&f[l][r][A[i]]<=v){
if(!in[A[i]])q[R++]=A[i],in[A[i]]=1;
i++;
}
for(d=0;d<4;d++){
if(!to[k][d])continue;
int nxt=to[k][d];
if(f[l][r][nxt]==-1||f[l][r][nxt]>v){
f[l][r][nxt]=v;
if(!in[nxt])q[R++]=nxt,in[nxt]=1;
}
}
}
for(i=0;i<R;i++)in[q[i]]=0;
}
void solve(){
rd(t);rd(m);rd(n);
memset(f,-1,sizeof(f));
int i,j,k,ans=-1;
for(i=1;i<=n;i++)scanf("%s",mp[i]+1);
for(i=1;i<=n;i++){
for(j=1;j<=m;j++){
if(mp[i][j]>='1'&&mp[i][j]<='9'){
BFS(i,j);num[mp[i][j]-'0']=id[i][j];
}
}
}//bfs部分不会超时的
for(i=t;i>=1;i--){
for(j=i;j<=t;j++)work(i,j);
}
for(i=1;i<=tot;i++){
if(~f[1][t][i])Min(ans,f[1][t][i]);
}
printf("%d\n",ans);
}
int main(){
// freopen("robot.in","r",stdin);
// freopen("robot.out","w",stdout);
solve();
return 0;
}
▲19:44:02 UOJ 109 APIO2013 出题人/提交答案 这道题真有意思~
①卡floyd很简单 n>100的空图即可
②卡bellmanford 加了一个负环进去,但要保证起点不能到达这个负环,这样它就在每次询问迭代n-1次 count计数为q*m*(n-1).
③卡dijkstra 这个好难想啊!!! 这里有个坑.
第二小题:
啊这个随便出一组数据至少可以得11分!多么痛的领悟.
出一个完全图就可以T掉了..
出一个二分图就可以过了...恩..
2017-02-25 周六(115)
▲11:27:38 UOJ108 APIO2013 T2 道路费用 最小生成树/暴力枚举/YY
首先考虑暴力做法:因为K很小,所以可以2^K暴力枚举有哪些边会在最终的MST上,选中之后再强制选择这些边,求一遍MST,选中的边(a,b)产生的权值是m条边中没在MST里可以联通a,b的最小边权值.复杂度为O(2^K*m*K).可以拿到一半分~
正解:K还是挺小的,所以我们还是暴力枚举,但现在求MST需要优化一下了:边有30万条,选中的边最多只有20条,也就是很多边是无论在K中选择哪几条边都会在最后的MST里,所以我们一开始选出这些边,然后缩点,会得到K+1联通块,把每个块看成一个点,然后再求MST即可.复杂度O(2^K*K^2).
▲15:59:03 QTREE6 LCT版本 还是构出两棵树,因为LCT支持切边和连边,所以可以维护相同颜色的联通块.那么问题就成了:有连边和删边操作,求一个点所在联通块大小.这就是对LCT的扩展.我们开一个新数组s[x]记录x的虚儿子的信息.合并时,关于x的信息来自 x的实儿子和虚儿子和自己.并且在access时,注意修改:把t从虚儿子里删掉,把ch[x][1]加到虚儿子里.
▲18:36:39 QTREE7 每个几点有黑白两色,和权值,现在操作有翻转一个点的颜色,修改一个点的权值,询问一个和一个点相连的点中权值最大值. 此题和上题类似,只要开一个set来维护虚儿子的信息即可.

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #include<iostream> 5 #include<set> 6 using namespace std; 7 const int M=1e5+5; 8 const int oo=2e9; 9 int v[M],n,m,ec=1,head[M],to[M<<1],nxt[M<<1],par[M]; 10 inline void rd(int &res){ 11 res=0;int k=1;char c; 12 while(c=getchar(),c<48&&c!='-'); 13 if(c=='-'){k=-1;c=getchar();} 14 do res=(res<<1)+(res<<3)+(c^48); 15 while(c=getchar(),c>=48); 16 res*=k; 17 } 18 inline void Max(int &x,int y){if(x<y)x=y;} 19 void print(int x){ 20 if(!x)return ; 21 print(x/10); 22 putchar((x%10)^48); 23 } 24 void sc(int x){ 25 if(x<0){x=-x;putchar('-');} 26 print(x); 27 if(!x)putchar('0'); 28 putchar('\n'); 29 } 30 struct LCT{ 31 int fa[M],ch[M][2],val[M],w[M];//s[x] 记录x的虚儿子 32 multiset<int>s[M]; 33 multiset<int>::iterator it; 34 void Up(int a){ 35 if(!a)return; 36 val[a]=w[a]; 37 if(ch[a][0])Max(val[a],val[ch[a][0]]); 38 if(ch[a][1])Max(val[a],val[ch[a][1]]); 39 if(s[a].size())Max(val[a],*(--s[a].end()));//LCT子树信息=LCT的实儿子+虚儿子+自己 的和 40 } 41 bool chk(int a){return ch[fa[a]][0]==a||ch[fa[a]][1]==a;} 42 void Rotate(int x){ 43 int y=fa[x],z=fa[fa[x]],son; 44 bool a=ch[y][1]==x,b=ch[z][1]==y; 45 son=ch[x][a^1]; 46 if(chk(y))ch[z][b]=x;fa[x]=z; 47 ch[y][a]=son;fa[son]=y; 48 ch[x][a^1]=y;fa[y]=x; 49 Up(y); 50 } 51 void Splay(int x){ 52 int y,z; 53 while(chk(x)){ 54 y=fa[x],z=fa[fa[x]]; 55 if(chk(y)){ 56 if(ch[y][0]==x^ch[z][0]==y)Rotate(x); 57 else Rotate(y); 58 } 59 Rotate(x); 60 } 61 Up(x); 62 } 63 void Access(int a){ 64 for(int t=0;a;t=a,a=fa[a]){ 65 Splay(a); 66 if(t){ 67 // it=s[a].lower_bound(val[t]); 68 // if(it!=s[a].end()) 69 s[a].erase(s[a].lower_bound(val[t])); 70 } 71 if(ch[a][1]){ 72 s[a].insert(val[ch[a][1]]); 73 } 74 ch[a][1]=t;Up(a); 75 } 76 } 77 int findrt(int a){ 78 Access(a);Splay(a);//一直往前找 79 while(ch[a][0])a=ch[a][0]; 80 return a; 81 } 82 void link(int a,int b){//b是fa 83 Access(b);Splay(b);// 84 Access(a);Splay(a); 85 ch[b][1]=a; 86 fa[a]=b; 87 Up(b); 88 } 89 void cut(int a){//把a和它父亲之间的边剪断 90 Access(a);Splay(a); 91 fa[ch[a][0]]=0; 92 ch[a][0]=0; 93 Up(a); 94 } 95 int qry(int a){//求a所在的块的大小 注意根有可能不是同一个颜色,要特判 96 int b=findrt(a); 97 // Access(b); 98 Splay(b); 99 if(v[b]!=v[a])return val[ch[b][1]];// 100 return val[b]; 101 } 102 void upd(int a,int b){ 103 Access(a);Splay(a); 104 w[a]=b; 105 Up(a); 106 } 107 }T[2]; 108 void ins(int a,int b){ 109 to[ec]=b;nxt[ec]=head[a];head[a]=ec++; 110 to[ec]=a;nxt[ec]=head[b];head[b]=ec++; 111 } 112 void dfs(int x,int pa){ 113 par[x]=pa; 114 T[0].val[x]=T[1].val[x]=-oo; 115 for(int i=head[x];i;i=nxt[i]){ 116 if(to[i]==pa)continue; 117 int y=to[i],c=v[to[i]]; 118 dfs(y,x); 119 T[c].s[x].insert(T[c].val[y]);//一开始只有虚的 120 T[c].fa[y]=x; 121 } 122 T[0].Up(x); 123 T[1].Up(x); 124 } 125 void solve(){ 126 int i,j,k,a,b,c,op; 127 T[0].val[0]=T[1].val[0]=-oo; 128 rd(n); 129 for(i=1;i<n;i++){ 130 rd(a);rd(b);ins(a,b); 131 } 132 for(i=1;i<=n;i++)rd(v[i]); 133 for(i=1;i<=n;i++)rd(T[0].w[i]),T[1].w[i]=T[0].w[i]; 134 dfs(1,0); 135 rd(m); 136 while(m--){ 137 rd(op);rd(a); 138 if(!op){ 139 sc(T[v[a]].qry(a)); 140 } 141 else if(op==1){ 142 T[v[a]].cut(a); 143 if(par[a])T[v[a]^1].link(a,par[a]); 144 v[a]^=1; 145 } 146 else{ 147 rd(b); 148 T[0].upd(a,b); 149 T[1].upd(a,b); 150 } 151 } 152 } 153 int main(){ 154 // freopen(".in","r",stdin); 155 // freopen("my.out","w",stdout); 156 solve(); 157 return 0; 158 }
2017-02-26 周日(117)
▲20:12:04 HDU6017 Girls Love 233 DP
①只有2,3两种字符 ②组成的串为"233"(我表示:23333( ̄︶ ̄)),所以串之间是不相交的,而且2是其中较为特殊的字符 ③交换方式为相邻交换.
从以上3点可以得到一些结论:
①交换完的2的相对位置不改变的!!!
②根据相邻的2之间的距离判断233的个数.
③每次交换一定是交换相邻两个不同的数字
所以我们得到一个思路:把2抽出来,考虑前i个2,用了j次交换,第i个2在位子k上的最多233个数.转移只要考虑上一个2的位置即可,如果位置差超过2,那就多了一个233.可以用前缀和优化,复杂度O(n^3)
▲22:12:46 QTREE5 每个点有黑白两色,现有两种操作:①改变一个点颜色 ②求与x最近的白色点的距离.
树的点分治!!点分治大法好~!树的点分治可以保证每个点只被计算logn次,而且能包括x和任意一个点的信息.
那么借助点分治来统计信息回答询问.先进行一遍点分治,把每个点对应的每个重心求出来,然后连边,每个重心建一个堆来维护它的子树里的dis最值情况.对于更新操作,只要考虑黑变白,记录每个点是不是已经在重心的堆里,如果没有就加入.在求某个堆的白点的最值时,把堆顶的黑色点进行标记即可.
2017-02-28 周二(119)
▲10:43:15 CTSC2010 D1T1 星际旅行 YY/贪心 别问我是怎么想的..这种复杂的思路还是不想为妙..其实我的思路和正解的也差不多,只是实现起来略复杂了一点.
先求出以1为根每个从每个子树下去,再回来的最多边数.对于一个终点i,相当于i到根上每个点(除了根节点)都多了一次出去的机会,只要逐个判断每个能不能再出去即可.复杂度O(n).(为什么n是五万!!!)
▲20:46:58 CTSC2010 D1T2 三国围棋擂台赛 【调试毁人生!!(╯﹏╰)(╯﹏╰)】博弈+状压DP 记录当前三队剩余人员的情况和现在获胜的选手以及接下来要上场的队伍.不进行优化,时间复杂度为O(6*n^2*2^3n) 当n=7显然过不掉!!但是由于题目给出了条件:指定了第一位选手,所以可以只要记录每队剩下的六个人即可.这样时空复杂度刚好!!



