1.本周学习总结(0--2分)
1.思维导图
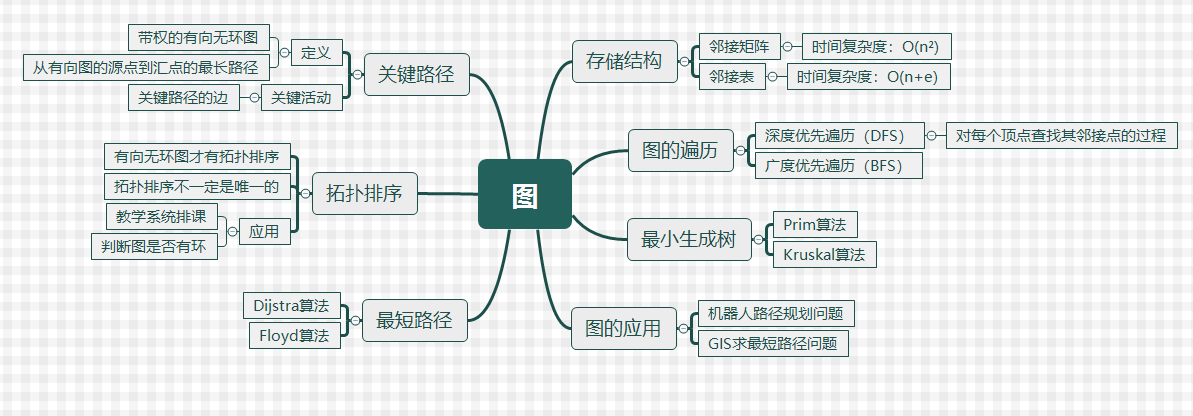
2.谈谈你对图结构的认识及学习体会。
这章学习了图,学习了图的两种存储结构:邻接矩阵和邻接表。这两种存储结构都用到了之前学c时学到的结构体,将结构体充分运用。知道了图的两种遍历方法:深度优先遍历(DFS)和广度优先遍历(BFS)。深度优先遍历是一个对每个结点查找其邻接点的过程,而广度优先遍历则搜索了所有节点。
通过学习Prim算法和Kruskal算法,解决了最小生成树问题。在学习Prim算法的同时,还提到了贪心算法,之前学习的贪心算法只能解决局部最优的问题,所以最小生成树的问题不可以用贪心算法来做。
学习最短路径时,先学的Dijstra算法,但是Dijstra算法存在只能解决最短路径,而不能解决最长路径的问题,由此引进了Floyd算法,在满足最小路径查找的同时也能满足最长路径的查找。
拓扑排序和关键路径都是对有向无环图的操作。拓扑排序可以用来判断一个有向图是否有环,还可以解决教学系统中的排课问题;关键路径则是用来解决最短工时的问题。
2.PTA实验作业(6分)
2.1.7-1 图着色问题
图着色问题是一个著名的NP完全问题。给定无向图G=(V,E),问可否用K种颜色为V中的每一个顶点分配一种颜色,使得不会有两个相邻顶点具有同一种颜色?
但本题并不是要你解决这个着色问题,而是对给定的一种颜色分配,请你判断这是否是图着色问题的一个解。
2.1.1设计思路(伪代码)
//设计思路
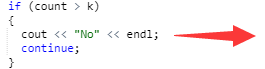
先建一个无向图的邻接矩阵。在每次判断解是否正确的过程中:先判断使用的颜色是否为k种,是,则继续操作,反之,输出“No”进入下一轮循环;用双重for循环判断每个结点的临边颜色是否符合要求。
//伪代码(主函数)
定义三个整型变量v、e、k、n,分别用于存放结点数、边数、颜色数,和 解的数量;
输入v、e、k;
定义一个MGraph型变量G;
利用CreatMGrap函数创建无向图;
输入解的数量n;
while n-- do
定义int型变量:flag=1,用于控制解不正确时的情况;num数组,用于存储各个结点的颜色;count=0,用于计算各个接中使用的颜色数量;hash数组,用于控制颜色数量的计算;
for i=0 to G.n do
输入num[i];
if hash[num[i]]等于0 then //num[i]颜色没出现过时
hash[num[i]]++;
count++;
end if
end for
if count的值与k不相等时 then
输出“No”
continue进入下一轮循环
end if
for i=0 to G.n do
for j=i to G.n do //无向图的邻接矩阵关于对角线对称,所以只要判断半个邻接矩阵
if i与j不相等 then
if i与j结点的颜色相同 且 i与j结点间有边 then
输出“No”
flag=0
break
end if
end if
end for
if flag=0 then
break
end if
end for
if flag=1 then
输出“Yes”
end if
end while
2.1.2代码截图(注意,截图,截图,截图。不要粘贴博客上。)


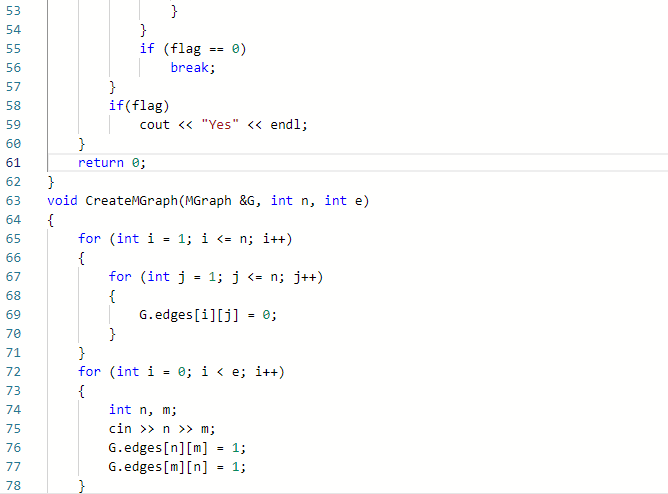
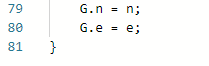
2.1.3本题PTA提交列表说明。

- Q1:第一次提交,是把判断解是否正确的那一部分写成一个函数的,结果提交上去显示答案错误。当时以为我的函数有什么问题,就把函数拆了,直接写到主函数里头,结果还是答案错误。
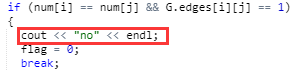
- A1:我想着代码没问题啊,调试也没毛病,突然,想到答案错误还有一种情况:输出的问题,看一眼题目要求,好吧,yes和no的首字母要大写,我没大写。
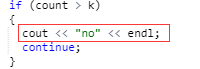
- Q2:然后,改完以后,部分正确,还有两分不知道错在哪,提示的是有小于k种颜色的情况错误。

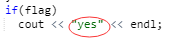
- A2:当时在想,我的做法小于k种颜色的情况也可以正确判断啊,为什么会显示这个错误。当时舍友在一边,我就问她着色的时候可不可以不用到k种颜色这么多。她说,当然可以啊。然后,我就很纳闷,到底哪儿错了。后来抱着试一试的心态,将使用的颜色小于k的情况也当走是错的,结果就过了。

2.2 7-6 修建道路
N个村庄,从1到N编号,现在请您兴建一些路使得任何两个村庄彼此连通。我们称村庄A和B是连通的,当且仅当在A和B之间存在一条路,或者存在一个存在C,使得A和C之间有一条路,并且C和B是连通的。
已知在一些村庄之间已经有了一些路,您的工作是再兴建一些路,使得所有的村庄都是连通的,并且兴建的路的长度是最小的。
2.2.1设计思路(伪代码)
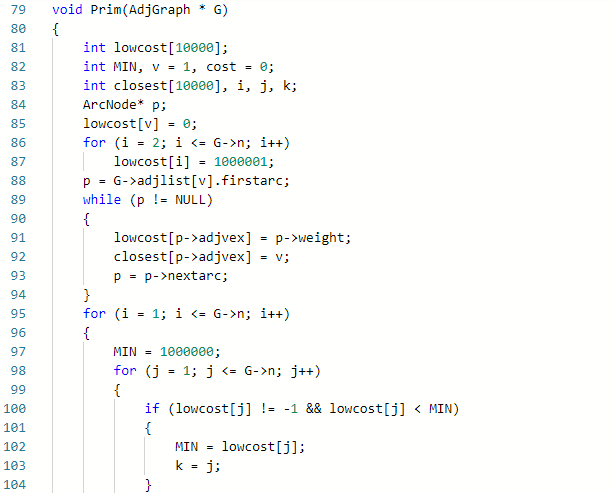
//伪代码(Prim函数)
定义一个int型数组lowcost[],变量MIN用于存放最小值,v,赋初值为1,cost用于计算花费,赋初值为0;
定义一个int型数组closest[],用于存放最近的结点,变量i,j,k,用于循环中
定义一个ArcNode型变量p
将0赋值给lowcost[v]
for i=2 to 图的节点数 do
lowcost[i]=10000001 //赋初值,令数组的初值最大
end for
将G->adjlist[v].firstarc的值赋给p
while p不为空 do
将p->weight的值赋给lowcost[p->adjvex]
将v的值赋给closest[p->adjvex]
令p等于p指向的下一个结点
end while
for i =1 to 图的节点数 do
赋初值1000000给MIN
for j=1 to 图的结点数 do
if lowcost[j]不等于-1 且 小于MIN then
将 lowcost[j]的值赋给MIN
将j的值赋给k
end if
end for
将MIN的值累加给cost
lowcost[k]=-1
将G->adjlist[k].firstarc的值赋给p
while p不为空 do
if p->weight小于lowcost[p->adjvex] 且 lowcost[p->adjvex]不等于-1 then
将p->weight的值赋给lowcost[p->adjvex]
将k的值赋给closest[p->adjvex]
end if
令p等于p指向的下一个结点
end while
end while
输出cost
2.2.2代码截图(注意,截图,截图,截图。不要粘贴博客上。)



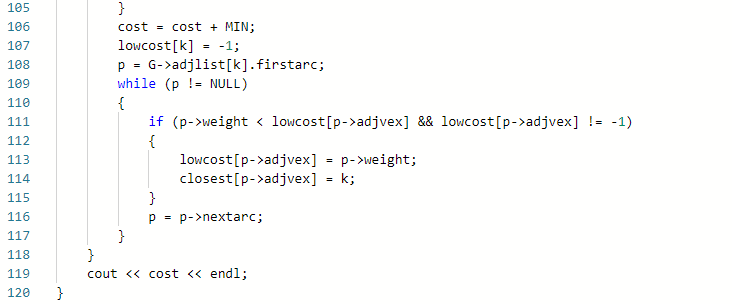
2.2.3本题PTA提交列表说明。

- Q1:这题答案错误,一开始没发现什么毛病,该赋值的也赋值了,后来无意间发现,好吧,赋初值的位置放错了。

- A1:改过来之后就对了。
2.3 7-7 旅游规划
有了一张自驾旅游路线图,你会知道城市间的高速公路长度、以及该公路要收取的过路费。现在需要你写一个程序,帮助前来咨询的游客找一条出发地和目的地之间的最短路径。如果有若干条路径都是最短的,那么需要输出最便宜的一条路径。
2.3.1设计思路(伪代码)
//伪代码(Dijkstra函数)
定义int型变量v,i,MIN1,MIN2
定义ArcNode型变量p
定义int型数组dist1[1000]、path[1000]、dist2[1000]
定义一个int型静态局部变量数组visted[1000]
for i=0 to 图的节点数 do
dist1[i]=100000
dist2[i]=100000
path[i]=-1
end for
将Begin的值赋给v
将0分别赋给dist1[v]和dist2[v],将v赋给path[v]
while 1 do
将100000分别赋给MIN1和MIN2
for i=0 to 图的结点数 do
if dist1[i]的值小于MIN1 且 visted不等于1 then
if dist1[i]的值小于MIN1 或者 dist2[i]的值小于MIN2 then
将dist1[i]的值赋给MIN1
将dist2[i]的值赋给MIN2
将i的值赋给v
end if
end if
end for
if v等于END then
退出循环
end if
visted[v]=1
将G->adjlist[v].firstarc的值赋给p
while p不为空时 do
if p->length与diat1[v]的和 小于等于 dist1[p->adjvex] then
if p->length与diat1[v]的和 小于 dist1[p->adjvex] 或者 p->price与diat2[v]的和 小于 dist2[p->adjvex] then
将p->length与diat1[v]的和赋给dist1[p->adjvex]
将p->price与diat2[v]的和 赋给dist2[p->adjvex]
将v的值赋给path[p->adjvex]
end if
end if
p等于p指向的下一个结点
end while
end while
输出dist1[v]和dist2[v]的值
2.3.2代码截图(注意,截图,截图,截图。不要粘贴博客上。)

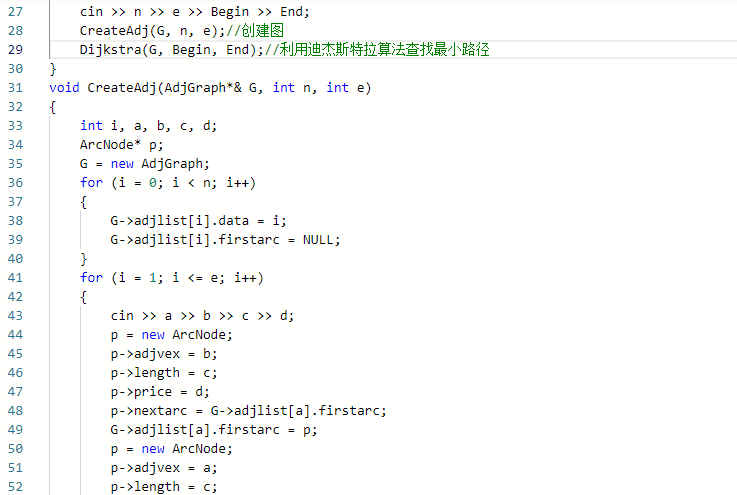
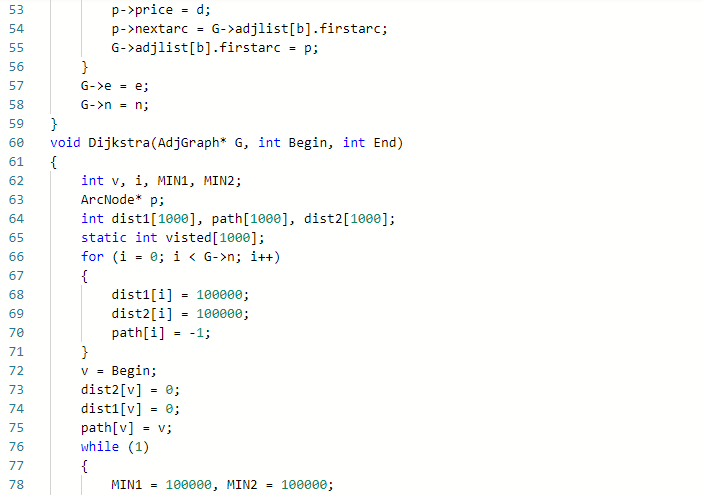
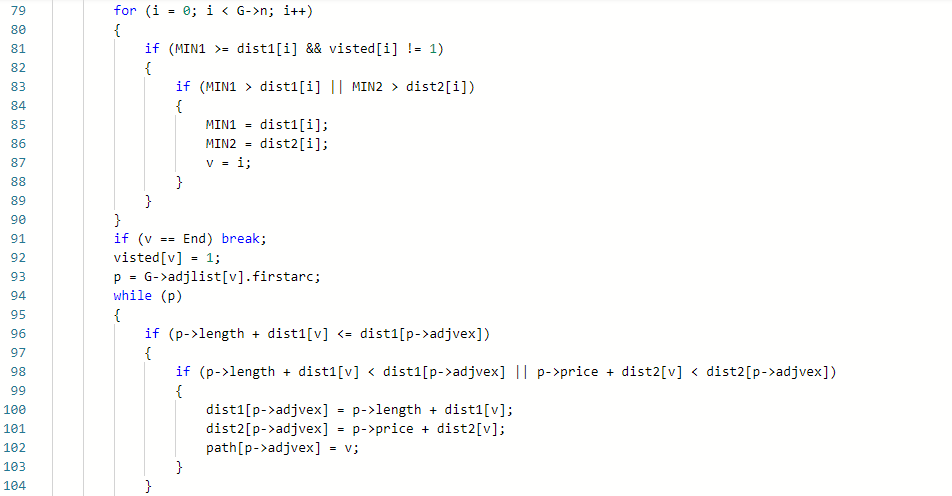

2.3.3本题PTA提交列表说明。

- 这题主要是关于迪杰斯特拉算法的一个应用。代码基本都是照着书上的代码修修改改完成的。然后调试什么的都在VS上完成了。
3、上机考试错题及处理办法(-2--2分)
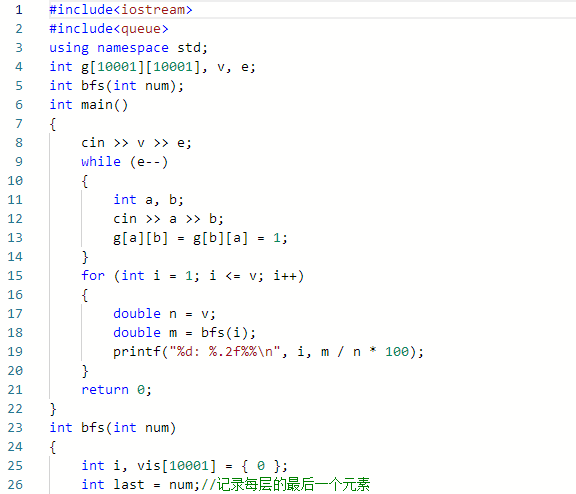
- 当时上机考试的时候,因为时间问题和对这章知识的不熟悉,只做了两道题(两道题都做出来了)。当时还剩几分钟的时候看了一下六度空间的题目,当时代码打了一半半时间就到了,就没打完,就把回来后打的代码贴上来。
//解题思路
利用广度优先遍历的算法来找到距离小于6的结点个数,来算出百分比
//伪代码(bfs函数)
定义int型变量i,数组vis[10001],并赋初值为0
定义int型变量last,令其等于num(用来记录每层的最后一个元素);tail,用于记录每层压入时的结点,level,并赋初值为0;count赋初值为1
定义一个int型队列q
将num入队
将1赋给vis[num]
while q不为空时 do
将队头的值赋给num
出队
for i=1 to v do
if g[num][i]等于1 且 vis[i]等于0 then
count++
将1赋给vis[i]
将i入队
将i 赋给tail
end if
end for
if last等于num then //弹出的x等于当前层的最后一个元素
level++
将tail的值赋给last
end if
if level的值为6时 then
退出循环
end if
end while
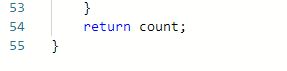
将count的值返回主函数




 浙公网安备 33010602011771号
浙公网安备 33010602011771号