P4363 [九省联考2018]一双木棋chess（轮廓线状压）

P4363 [九省联考2018]一双木棋chess

这两天学了这个。

是轮廓线状压的或许算是裸题。

关键在于怎么压状态。

题意

• 有一个 \(n \times m\) 的棋盘，两个人轮流下棋。

• 一个位置可以落子当且仅当这个位置的左侧和上面都有棋子。

• 两个人落在对应的位置会收获各自的贡献值。

• 最大化自己的得分减去对方的得分。

做法

博弈论？

是有 max_min搜索还有一些别的做法的。

max_min搜索

看眼数据范围，都是 \(10\) 以内的。

于是考虑状压。

问题随之而来：如何存状态？

由于落子是有限制的，所以需要考虑在什么情况下可以落子。

由于落子是合法的需要满足左边和上边都有棋子，于是在整个过程中必然会有这样的情况：

可以发现这样的轮廓一定是连续的。

于是这就是我们需要的轮廓线。

可以考虑存储右下角的轮廓线作为状态。

如何存储呢？

首先这个轮廓线的长度肯定是 \(n+m\) 的。

我们用 \(0\) 来表示横边，用 \(1\) 来表示竖边。

可以举个例子：

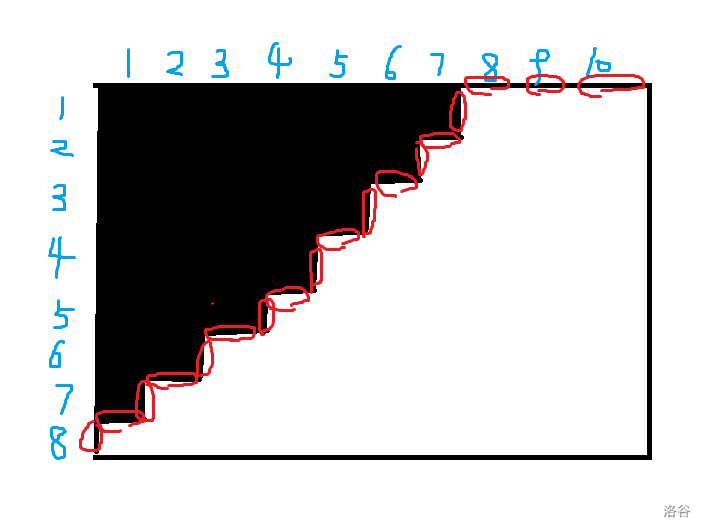
对于当前的状态，从右上角开始，向左下角延伸，如果有横边那么当前位就是 \(0\)，有竖边就是 \(1\)；

所以状态串就是 \(000101010101010101\)

之后对于状态的判断以及转移过程，都可以利用这个轮廓线。

可以发现，经过这样的状压之后，判断是否可以落子的条件就变成了：是否存在一个位置，满足串中有 \(01\) 这样的两位，如果有，那么就可以落子。

落子以后，该位置的 \(01\) 就会变成 \(10\)。

对于转移过程中的具体操作，由于需要判断状态串中是否存在 \(01\)，可以采用一种手法：

if(((now>>i)&3)!=1)continue;

由于 \(3\) 的二进制是 \(011\) ，如果也就是判断是否存在 \(01\)的情况。

之后改变状态：

int nxt=now^(3<<i);

之后起始状态和终止状态就很明显了：

起始状态：\(000...00111...11\)

终止状态：\(111...11000...00\)

之后就是关于如何 DP 的问题了。

其实这个事情是不好办的。

首先这个题目要求我们两个人都要走最优策略。

如果按照我们常规的 DP 思路的话，自然是要设 \(f[S]\) 为在 \(S\) 这个状态下可以获得多少得分差。

但是对于这种博弈论 DP 的题目是不可以这样做的。

由于两方都要采取最优策略，所以我们不得不考虑将来的行动对现在现在的影响。

如果正序 dp 的话也许会发生当前确实取到了最大值但是其实并不是最优策略。

于是我们可以考虑倒过来 dp。

可以假装我们可以一步看到结局，然后选择对自己最有利的状态。

显然棋盘被布满的状态下没有人可以获得新的分数，那么如果我们用 \(f[S]\) 表示从 \(S\) 轮廓线的状态距离游戏结束还能得多少分。

那么我们会发现，如果这个局面是先手下完以后形成的，那么如何这个局面如何转移的主动权显然是攥在后手的手里，所以此时这个 dp 值应该由所有后继状态的相对于先手最劣的状态转移过来，也就是所有的后继状态取个 \(\min\)。

如果是后手的话，dp值就应该是对于后手最劣的状态转移过来，也就是所有的后继状态取个 \(\max\)。

也就是第一个人想要最大化两者的差值，第二个人想要最小化这个差值。

//#define LawrenceSivan

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
#define re register
const int maxn=1e5+5;
#define INF 0x3f3f3f3f

int n,m;

int f[1<<21];

int a[15][15],b[15][15];

bool vis[1<<21];

int dfs(int now,int who){
	if(vis[now])return f[now];//记忆化搜索
	vis[now]=true;
	f[now]= who?-INF:INF;//先手取max，所以初始最小，后手取min，所以初始最大
	
	int x=n,y=0;
	for(re int i=0;i<n+m-1;i++){
		if((now>>i)&1)x--;
		else y++;
		if(((now>>i)&3)!=1)continue;
		int nxt=now^(3<<i);
		if(who)f[now]=max(f[now],dfs(nxt,0)+a[x][y]);
		else f[now]=min(f[now],dfs(nxt,1)-b[x][y]);
	}
	
	return f[now];
}

inline int read(){
    int x=0,f=1;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
    while(isdigit(ch)){x=x*10+(ch^48);ch=getchar();}
    return x*f;
}

int main(){
#ifdef LawrenceSivan
    freopen("aa.in","r",stdin);
    freopen("aa.out","w",stdout);
#endif
	n=read();m=read();
	for(re int i=0;i<n;i++){
		for(re int j=0;j<m;j++){
			a[i][j]=read();
		}
	}
	for(re int i=0;i<n;i++){
		for(re int j=0;j<m;j++){
			b[i][j]=read();
		}
	}
	
	vis[((1<<n)-1)<<m]=true;//倒过来DP，即从结束状态开始
	f[((1<<n)-1)<<m]=0;
	
	dfs((1<<n)-1,1);
	
	printf("%d\n",f[(1<<n)-1]);//最后找到开始状态下对应的答案



	return 0;
}