替罪羊树学习笔记
替罪羊树
前言:
首先平衡树写法真的是太多了
据不完全统计
比较知名的有 红黑树 (\(RB\_Tree\)),替罪羊树,\(Treap\),\(fhq\_Treap\) , \(Splay\) , \(AVL\) , \(SBT\) , \(0/1\ Trie\) 等等
自然我是没有时间把这些玩意都学一遍的
而且有些不当人的玩意确实不是人学的
今天要说说替罪羊,也是近期学会的。
简介
替罪羊树是计算机科学中,一种基于部分重建的自平衡二叉搜索树。在替罪羊树上,插入或删除节点的平摊最坏时间复杂度是 \(O(log n)\) ,搜索节点的最坏时间复杂度是 \(O(log n)\)。——百度百科
首先我们都知道,\(Treap\) , \(Splay\) ,等平衡树都是需要旋转操作来维持树的平衡结构。
带旋转的平衡树一般存在以下问题:
-
可持久化几乎就是不可能(\(Treap\) 可以用 \(fhq\_Treap\) 来搞,而且貌似还很主流)(虽然替罪羊树可持久化也极其困难,貌似就算实现了复杂度也是假的)
-
对于一个平衡树的每个节点上维护一个集合,存储子树内所有的数。此时一次旋转操作的代价可能会达到 \(O(n)\) ,传统的旋转平衡树就无法发挥作用
于是,我们就需要一些不带旋转操作的平衡树。
作为重量平衡树的一种的替罪羊树就满足这样的条件。
原理
替罪羊是一种基于暴力重构来维持树的平衡的数据结构。
我们定义一个平衡树因子 \(\alpha\) ,对替罪羊树的每个节点 \(t\) ,我们都需要满足:\(\max(l->size,r->size )<=\alpha\times t->size\)其中 \(l\) , \(r\) 分别是 \(t\) 的左右子树。这个性质称为平衡性质。
一旦出现了违背这个满足性质,就把这棵子树暴力拍扁重构。
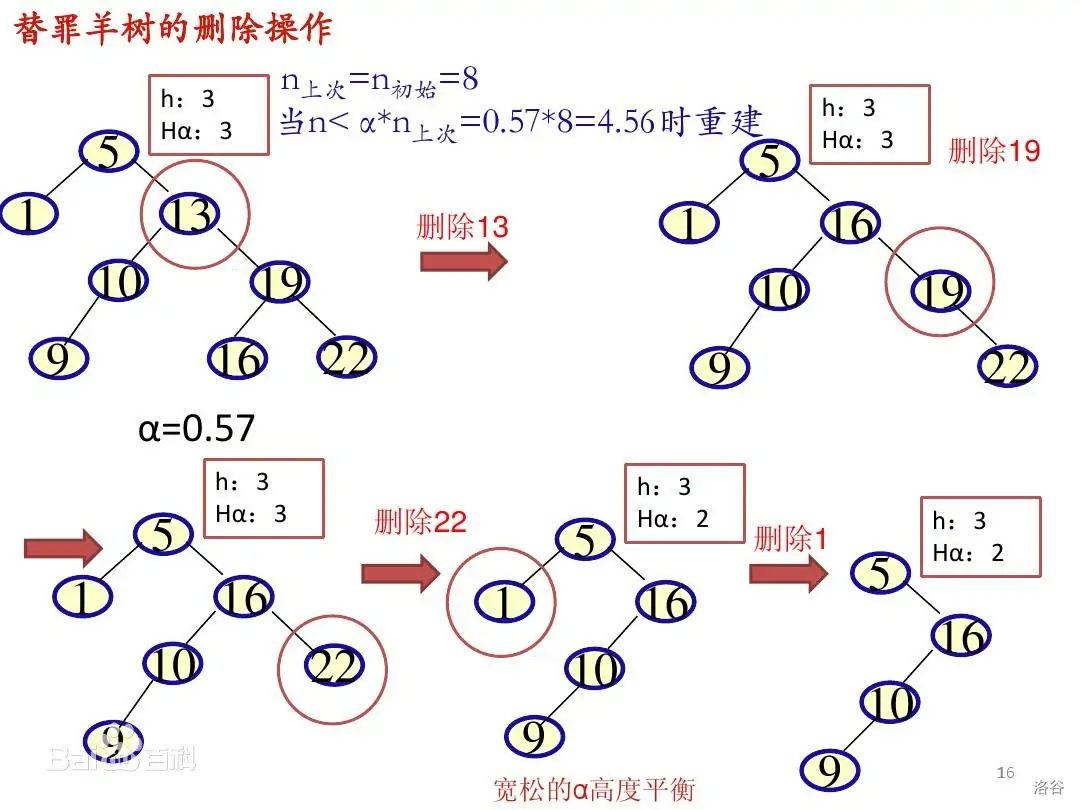
(图片来自百度)
实现方法
重构
拍扁具体是什么意思呢?
我们只需要对需要进行重构的子树执行一次中序遍历,然后把它存到一个数组里(为了方便下面我们使用了\(std::vector\))
然后我们再每次取中点,向左右两边递归建树就好了。
代码实现很简单:
void dfs(node* o,vector<node*> &v){
if(o==null)return;
dfs(o->l,v);
if(!o->del)v.push_back(o);
dfs(o->r,v);
if(o->del)delete o;
}
node* build(vector<node*> &v,int l,int r){
if(l>=r)return null;
int mid=(l+r)>>1;
node *o=v[mid];
o->l=build(v,l,mid);
o->r=build(v,mid+1,r);
o->update();
return o;
}
void rebuild(node* &o){
vector<node*> v;
dfs(o,v);
o=build(v,0,v.size());
}
关于复杂度
这样重构一次的时间复杂度为 \(O(n)\)(n为子树大小),但是实际上替罪羊树的单次插入时间复杂度并不会达到 \(O(nlogn)\),因为一个 \(size=t\) 的子树需要插入 \(Ω(t)\) 个点才会被重构,所以可以通过势能分析来证明替罪羊树的单次操作的均摊时间复杂度为 \(O(logn)\),具体证明这里不详细展开。
关于势能分析可以参考这篇文章.
关于 \(\alpha\) 的取值
一般来说,\(\alpha\) 的取值一般在 \(0.5 - 1\) 之间。
根据定义我们可以发现,当 \(\alpha\) 太小可能会导致重构次数太多,当 \(\alpha\) 太大可能会导致重构次数太少,导致树高度不平衡,在查找操作的时候会导致浪费大量的时间。
一般取 \(7\) 或者 \(7.5\) 就足够了。
关于写法
没错,我个 \(SB\) 又写了指针。
刚开始学的时候是跟着洛谷板子题第一页写的,但是那个题解有一些缺点,这个问题我们在下面会进行说明。
其实指针也蛮好写的。
结构体的定义如下:
struct node{
node *l,*r;
int val,size,cnt;//val 值 size存在的节点数 cnt 全部的节点数
bool del;
bool isbad(){
return l->cnt>alpha*cnt||r->cnt>alpha*cnt;
}
void update(){
size=!del+l->size+r->size;
cnt=l->cnt+r->cnt+1;
}
};
在上面的片段中,出现了存在的节点数和全部的节点数这样的变量,这也是一个需要强调的点,至于为什么这么写,这需要涉及到替罪羊树的一种基本操作。
至于使用了 \(new\) 来动态申请内存很慢这件事,我们可以使用手写内存池的方式,这样既快而且还可以节约空间
node mempol[maxn]; //内存池
node *tail; //tail为指向内存池元素的指针
node *bc[maxn]; //内存回收池(栈)
int bc_top; //内存回收池(栈)顶指针
node* newnode(int val) { //返回一个新节点
node* p=bc_top?bc[--bc_top]:tail++; //分配内存
p->l=p->r=null;
p->cnt=p->size=1;
p->val=val;
p->del=0;
return p;
}
不过最终我还是没有使用,如果有需要的话可以自行添加。
删除操作
我们在替罪羊树中的删除操作并不是把它真的从替罪羊树中删除,而是给要删除的节点打上一个标记,代表我们要把他删除了。
在统计的时候我们要分开统计。
真正的节点数(用于查排名之类的操作)
全部的节点数(用来判断是否需要重构)
其实网上还有很多写法,比如当一个子树中坏点太多了严重影响树的平衡,就也需要重构之类的事情。
这么写其实在一定程度上可以减少这种情况的发生。
值得一提的是,我这里写的删除操作并不是把某个值为 \(x\) 的节点删去,而是把排名为 \(x\) ,的节点删去,所以在 \(remove\) 之前,我们首先要进行一次查排名的操作。
void remove(node *o,int k){
if(!o->del&&k==o->l->size+1){
o->del=1;
o->size--;
return;
}
o->size--;
if(k<=o->l->size+!o->del)remove(o->l,k);
else remove(o->r,k-o->l->size-!o->del);
}
int main(){
null=new node;
root=null;
n=read();
while(n--){
op=read();x=read();
if(op==2)remove(root,Rank(root,x));
}
}
插入操作
对于插入操作,一般来讲是没什么可说的
void Insert(node* &o,int x){
if(o==null){
o=new node;
o->l=o->r=null;
o->del=false;
o->size=o->cnt=1;
o->val=x;
return;
}
else{
o->size++;
o->cnt++;
if(x>=o->val)insert(o->r,x);
else insert(o->l,x);
if(o->isbad())rebuild(o);
}
}
但其实这样是稍微有点问题的(虽然这并不影响你通过模板题)
我们可以发现这个片段:
else{
o->size++;
o->cnt++;
if(x>=o->val)insert(o->r,x);
else insert(o->l,x);
if(o->isbad())rebuild(o);
}
意思是如果发现了坏点我们就是直接重构。
其实会带来一些问题
如果在一颗子树内有很多坏点,而我们恰好最早发现的却是深度最大的一棵,于是我们很鸡儿蠢的从最底下开始一点一点一点的往上爬,一次一次一次的重构,导致其实这一个子树这么大一棵我们要重构到昏天黑地,直接导致有可能 \(T\) 飞。(然而模板题并不会)
于是我们可以考虑用一个指针记录一下深度最小的坏点,然后重构的时候直接把一整棵树全都重构了,这样就省下了大把的时间用来颓废
这里我的实现方式是用一个指向指针地址的指针来记录。
虽然这样看起来很鸡儿蠢
node *null,*root,**badtag;
void Insert(node* &o,int x){
if(o==null){
o=new node;
o->l=o->r=null;
o->del=false;
o->size=o->cnt=1;
o->val=x;
return;
}
else{
o->size++;
o->cnt++;
if(x>=o->val)Insert(o->r,x);
else Insert(o->l,x);
if(o->isbad())badtag=&o;
else if(badtag!=&null) o->cnt-=(*badtag)->cnt-(*badtag)->size;
}
}
void insert(node* &o,int x){
badtag=&null;
Insert(o,x);
if(badtag!=&null)rebuild(*badtag);
}
int main(){
null=new node;
root=null;
n=read();
while(n--){
op=read();x=read();
if(op==1)insert(root,x);
}
}
前驱与后继操作
这里的求前驱和求后继与别的平衡树略有不同
对于查找前驱,我们可以直接查找比它的排名低一位的元素;
对于后继,我们可以查找比它大1的元素的排名,再查找该排名所对的元素。
然后这样模板题的所有操作我们就都资瓷了!
int Rank(node *o,int x){
int ans=1;
while(o!=null){
if(o->val>=x)o=o->l;
else{
ans+=o->l->size+!o->del;
o=o->r;
}
}
return ans;
}
int kth(node *o,int x){
while(o!=null){
if(!o->del&&o->l->size+1==x)return o->val;
if(o->l->size>=x)o=o->l;
else{
x-=o->l->size+!o->del;
o=o->r;
}
}
}
int main(){
null=new node;
root=null;
n=read();
while(n--){
op=read();x=read();
if(op==5)printf("%d\n",kth(root,Rank(root,x)-1));
if(op==6)printf("%d\n",kth(root,Rank(root,x+1)));
}
return 0;
}
要说的就这么多了。
放一下模板题的代码:
CODE:
//#define LawrenceSivan
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define re register
const double alpha=0.7;
#define INF 0x3f3f3f3f
int n,op,x;
struct node{
node *l,*r;
int val,size,cnt;//val 值 size存在的节点数 cnt 全部的节点数
bool del;
bool isbad(){
return l->cnt>alpha*cnt||r->cnt>alpha*cnt;
}
void update(){
size=!del+l->size+r->size;
cnt=l->cnt+r->cnt+1;
}
};
node *null,*root,**badtag;
void dfs(node* o,vector<node*> &v){
if(o==null)return;
dfs(o->l,v);
if(!o->del)v.push_back(o);
dfs(o->r,v);
if(o->del)delete o;
}
node* build(vector<node*> &v,int l,int r){
if(l>=r)return null;
int mid=(l+r)>>1;
node *o=v[mid];
o->l=build(v,l,mid);
o->r=build(v,mid+1,r);
o->update();
return o;
}
void rebuild(node* &o){
vector<node*> v;
dfs(o,v);
o=build(v,0,v.size());
}
void Insert(node* &o,int x){
if(o==null){
o=new node;
o->l=o->r=null;
o->del=false;
o->size=o->cnt=1;
o->val=x;
return;
}
else{
o->size++;
o->cnt++;
if(x>=o->val)Insert(o->r,x);
else Insert(o->l,x);
if(o->isbad())badtag=&o;
else if(badtag!=&null) o->cnt-=(*badtag)->cnt-(*badtag)->size;
}
}
void insert(node* &o,int x){
badtag=&null;
Insert(o,x);
if(badtag!=&null)rebuild(*badtag);
}
int Rank(node *o,int x){
int ans=1;
while(o!=null){
if(o->val>=x)o=o->l;
else{
ans+=o->l->size+!o->del;
o=o->r;
}
}
return ans;
}
int kth(node *o,int x){
while(o!=null){
if(!o->del&&o->l->size+1==x)return o->val;
if(o->l->size>=x)o=o->l;
else{
x-=o->l->size+!o->del;
o=o->r;
}
}
}
void remove(node *o,int k){
if(!o->del&&k==o->l->size+1){
o->del=1;
o->size--;
return;
}
o->size--;
if(k<=o->l->size+!o->del)remove(o->l,k);
else remove(o->r,k-o->l->size-!o->del);
}
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+(ch^48);ch=getchar();}
return x*f;
}
int main(){
#ifdef LawrenceSivan
freopen("aa.in","r",stdin);
freopen("aa.out","w",stdout);
#endif
null=new node;
root=null;
n=read();
while(n--){
op=read();x=read();
if(op==1)insert(root,x);
if(op==2)remove(root,Rank(root,x));
if(op==3)printf("%d\n",Rank(root,x));
if(op==4)printf("%d\n",kth(root,x));
if(op==5)printf("%d\n",kth(root,Rank(root,x)-1));
if(op==6)printf("%d\n",kth(root,Rank(root,x+1)));
}
return 0;
}

 一种基于暴力重构的重量级平衡树
一种基于暴力重构的重量级平衡树

